» 詳しい使用方法や、エラーで展開できない際の対応方法などはこちら
力学アルゴリズムによる波のシミュレーション(面上の波)
このプログラムは、面上を伝わる波を、単純な力学アルゴリズムと数値積分法によって計算し、その結果をリアルタイムでアニメーション表示するVCSSLプログラムです。
なお、このプログラムは以下のプログラムの応用編です。先にそちらの方からお読みいただくと、内容がスムーズに把握できるかもしれません。
- [力学演算] 力学アルゴリズムによる波のシミュレーション(線上の波)
- [描画処理] 頂点配列によるモデルの変形アニメーション
- [モデリング] 頂点配列によるモデルの作成(四角形格子メッシュ形式)
使用方法
ダウンロードと展開(解凍)
まず、PC(スマホは未対応)で上の画面の「 ダウンロード 」ボタンを押してください。 するとZIP形式で圧縮されたファイルがダウンロードされます。
その後、ZIPファイルを右クリックして「すべて展開」や「ここに展開」などで展開(解凍)してください。 展開が成功すると、ZIPファイルと同じ名前のフォルダができ、その中にZIPファイルの中身が入っています。
» 展開がエラーで止まってしまう場合や、ファイル名が文字化けしてしまう場合は…
プログラムの起動
Windows をご使用の場合
上記でZIPファイルを展開したフォルダ内にある、以下のバッチファイルをダブルクリック実行してください:
もしプログラムを書き変えながら使いたい場合は、代わりに「 VCSSL_Editor__プログラム編集はこちら.bat 」を実行してください。
正常に起動できると、初回のみ、Java実行環境を入手するか等を尋ねられるので、適時答えて済ませると、プログラムが起動します。 2回目以降はすぐに起動します。
Linux 等をご使用の場合
ZIPファイルを展開したフォルダ内へコマンドライン端末で cd して、以下の通り入力して実行してください:
(プログラムの内容を書き変えながら使いたい場合は、代わりに VCSSL_Editor.jar を実行)
» javaコマンドが使用できない等のエラーが表示される場合は…
操作方法
画面上で、下記のマウス操作を行えます。
- 左ドラッグ … 視点の回転
- 右ドラッグ … 視点の平行移動
- ホイールスクロール … 拡大/縮小
題材解説
面上を伝わる波
「波」について、最も基礎的なものは、線(1次元)上を伝わる波です。しかし、日常的には「波」というと、水面などの面(2次元)上を伝わるものをイメージします。
シミュレーションでは、バネと質点による格子メッシュでモデル化
波を伝えるのは、弾性のある、つまり伸び縮みする媒質です。
このような弾性体をシミュレーションするにはいくつかの方法があります。簡単なのは、媒質を、バネで繋がった質点(質量のある点)で置き換える事です。そして弾性体の張力はバネの張力で、密度は質点の質量で表現します。
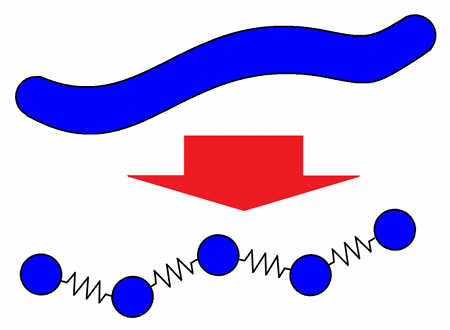
線(1次元)上の波をシミュレーションするなら、上図の通り、線上にバネを繋げるだけで済みます。一方、面(2次元)上を伝わる波の場合は、バネをメッシュ(網の目)のように張り巡らせ、格子点に質点を置いたモデルを用います。
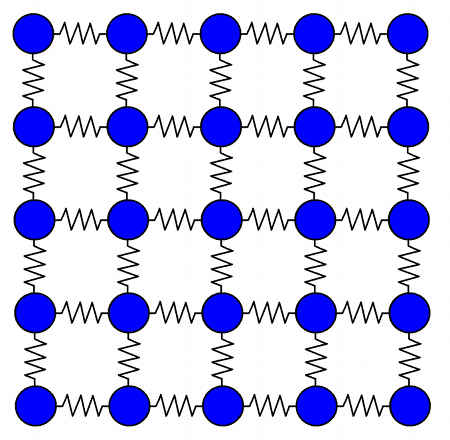
このようにモデルを設定すれば、媒質全体の運動は、前後左右の4つのバネから力を受ける、質点の運動として扱えます。
なお、メッシュはX-Y平面の方向に張っているとし、波の振動方向はZ軸のほうに取るものとします。
隣り合う1個の質点(とバネ)からは、Z値の差に比例する力を受ける
隣り合う1個の質点から受ける力については、線上の波をシミュレーションする場合と全く変わりません。 具体的には、以下のプログラムの解説ページで求めた通りです。求める詳しい手順については、以下のページをご参照下さい。
今回は、上記ページで求めた結果だけを用いる事とします。
即ち、「 隣り合う1個の質点からは、Z値の差に比例する力を、Z方向に受ける 」というものです。水平方向(ここではX/Y方向)の力はオーダーが小さいため、振幅があまり大きくない場合は、ほぼ無視できます。
具体的に式で記述すると、ある質点が、Z方向にバネから受ける力 F は以下のようになります:
\(F_{ある質点が、バネから受ける力} \simeq T dz/dL\)\( = T (z_{その隣の質点} - z_{ある質点})/dL\)
ここで T はバネの張力です。また dL は、質点間の距離であって、X方向に隣接する質点なら dx、Y方向に隣接する質点なら dy と記述します。格子は水平方向へはほぼ力を受けないため、dx と dy はほぼ定数と見なせます。
X方向およびY方向へのメッシュ全長を Lx, Ly とし、各方向への質点数を Nx, Ny とすると、dx と dy の値は:
\( dx = L_x / (N_x-1) \)
\( dy = L_y / (N_y-1) \)
質点の受ける力は、4つの隣接する質点(とバネ)から受ける力の合計
質点は、4つの質点(とバネ)と繋がっています。質点が力を受ける経路はこれだけです。従って、質点が受ける力は、これら4つの質点から受ける力の合計で求まります。
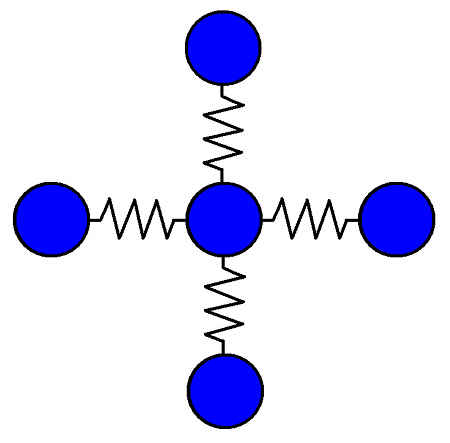
具体的に、ある質点がバネから受ける力を式で書くと:
\(F_{ある質点が、バネから受ける力} =\)\(T (z_{x方向の隣接質点1} - z_{ある質点})/dx\)
\(+ T (z_{x方向の隣接質点2} - z_{ある質点})/dx\)
\(+ T (z_{y方向の隣接質点1} - z_{ある質点})/dy\)
\(+ T (z_{y方向の隣接質点2} - z_{ある質点})/dy\)
と書けます。
端の処理(固定端、自由端)
上の式では、4つの隣接質点を前提としたもの、つまり端以外の質点に関するものです。
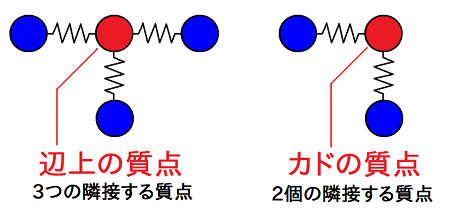
従ってメッシュの端、即ち辺上にある質点に関しては、上の式とは異なる特別な処理を行う必要があります。具体的に端をどう処理するかについては、次に述べる2つの方式があります。
一つは「 固定端 」というもので、端(辺上)の質点を固定してしまい、動かなくするという方式です。この場合、質点がバネから受ける力は、固定の抗力と釣り合って常に 0 となります:
\( F_{固定端がバネから受ける力} = 0 \)もう一つは「 自由端 」というもので、端の質点であっても、隣接する3個(辺上の場合)または2個(カドの場合)の質点とのバネから力を受けるとするものです:
\( F_{自由端がバネから受ける力} = 隣接する2または3個の質点から受ける力の和 \)
速度に比例する摩擦力で、減衰効果を加える
このままでは、全体でエネルギーが保存しているため、波がいつまでたっても消えません。しかし現実では、波はいずれ減衰して消えてしまいます。
このような減衰効果は、モデルによってメカニズムが異なります。最も簡単なのは以下のように、各質点に、速度に比例する摩擦力を加える事です。
\( F_{減衰効果付きの力} = F_{バネから受ける力} - f v \) … (6)
小文字の v は質点の速度です。小文字の f は摩擦力の係数で、この値が大きいほど波の減衰が強くなります。摩擦力は、速度と逆向きに作用するため、項の符合にマイナスが付いています。
数値積分によって運動を解く
個々の質点の受ける力が求まったので、あとはニュートンの運動方程式を立てて数値積分すれば、質点の運動が求まります。個々の質点の運動方程式は、加速度を a 、質点の質量を m として:
\( m a = F \)
と置けます。ここで加速度 a は速度 v の微分 dx /dt であり、さらに速度 v は位置 y の微分 dy / dt なので、以下の 2 式の形に直します。
\( dv / dt = F / m \) … (7)
\( dx / dt = v \) … (8)
あとはこれらの連立微分方程式を解けば良いのですが、シミュレーションで数値的に解くために、時間変数 t を細かい区間 Δt に区切り、数値積分法を用いて解きます。
最も単純なのは、Euler(オイラー)法と呼ばれる数値積分法です。 これは、時間区間 Δt 内では、v や F がほぼ変わらないと見なす方法です。こうすると、
\( \Delta v / \Delta t = ( v_{t+1} - v_t ) / \Delta t = F_t / m \) … (9)
\( \Delta x / \Delta t = ( x_{t+1} - x_t ) / \Delta t = v_t \) … (10)
となり、現在の時刻の状態から、次の時刻の状態を求める漸化式が得られます:
\( v_{t+1} = v_t + (F_t/m) \Delta t \) … (11)
\( x_{t+1} = x_t + v_t \Delta t \) … (12)
ただし、Euler法はあまり精度が良くありません。科学技術計算で要求される精度を出したければ、4次Runge-Kutta法(RK4)など、もっと高精度の数値積分法を用いる必要があります。
しかし、Euler法を次のように一部改変するだけで、RK4ほどではありませんが、精度を上げる事ができます:
\( v_{t+1} = v_t + (F_t/m) \Delta t \) … (13)
\( x_{t+1} = x_t + v_{t+1} \Delta t \) … (14)
このように、位置の更新に、古い速度ではなく、新しい速度を用いるだけです。こうしておく事で Symplectic数値積分の一種となり、エネルギーが振動的に保存するようになると共に、精度自体もEuler法より向上します。
3DCGでの描画方法
以上で、メッシュの運動を力学的アルゴリズムでシミュレーションする方法は求まりました。続いて、それを3DCGで画面に描画する方法について解説します。
ここでは、要点のみを抜き出して解説します。より詳しい解説は、以下のページをご参照下さい。
- [3Dモデルの作成] 頂点配列によるモデルの作成(四角形格子メッシュ形式)
- [アニメーション] 頂点配列によるモデルの変形アニメーション
四角形格子メッシュ(QUADRANGLE_GRID)形式の頂点配列
まずモデルの作成についてですが、今回のような格子メッシュ状に並ぶ座標値からは、簡単に3Dモデルを作成する事ができます。
それにはまず、四角形格子メッシュ(QUADRANGLE_GRID)形式という特定の形で、メッシュ頂点の座標を格納した「 頂点配列 」を用意します。
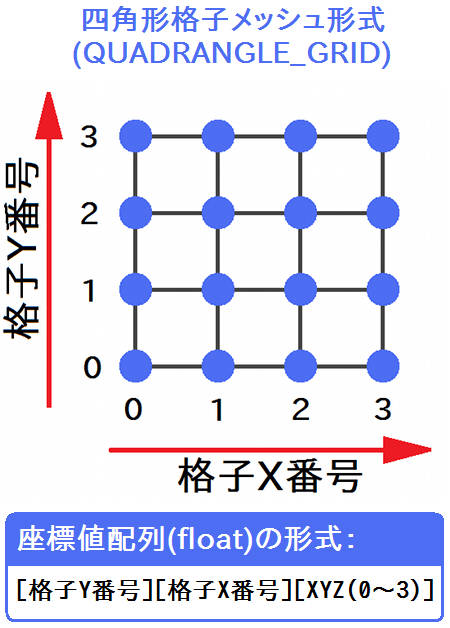
この形式の頂点配列は、3次元のfloat配列で用意します。
左と中央の次元は、格子のYとX方向の番号を意味します。具体的な番号は上図を参照してください。なお、[ X番号 ][ Y番号 ]ではなく、[ Y番号 ][ X番号 ]である事にご注意ください。Y-Z方向やZ-X方向の格子を使う場合も、このようにインデックスが逆転します。
右の次元は、その格子点の座標値のX/Y/Zを意味する次元です。0がX、1がY、2がZに対応します。
上図からも見て取れる通り、この形式の頂点配列は、今回のような四角形のメッシュ構造を扱うのに非常に都合の良い形式となっています。
実際、今回のプログラムでは上の形式の頂点配列を作成し、それを単に描画時だけでなく、力学演算時にも流用しています。描画用と演算用でわざわざ別に配列を用意するメリットが、今回はあまり無いからです(描画メッシュよりも演算メッシュを細かく取りたい場合などは、別に用意する意味もあります)。
描画モデルの生成
頂点配列からモデルを生成するには、Graphics3D ライブラリの newModel( int format, float vertex[ ][ ][ ] ) 関数を使用します。引数のformatには、Graphics3Dライブラリに定義されている定数値 QUADRANGLE_GRID を指定します。続くvertexには頂点配列を指定します。なお、この関数は、頂点配列からモデルを生成し、そのモデルに固有の識別番号「 モデルID 」をint型で返します。
描画モデルの形状変更
今回はモデルの変形をアニメーションで描画する必要があるので、画面更新タイミングごとに、モデルに頂点配列を再設定する必要があります。これにはGraphics3D ライブラリの setModelVertex( int modelID, float vertex[ ][ ][ ], int format ) 関数を使用します。引数のmodelIDには、newModel関数が返したモデルIDを指定します。続くvertexには頂点配列を指定します。最後のformatには、ここでも QUADRANGLE_GRID を指定します。
3DCGプログラミングの詳細はガイドで
その他、3DCGの制御に関する基本的な解説は、下記のガイドで解説していますので、そちらをご参照下さい。
コード解説
コード全体
このプログラムのコード全体は少し長ですが、まずは全体を見てみましょう。以下の通りです。
coding UTF-8;
import Math;
import Graphics3D;
import graphics3d.Graphics3DFramework;
// グリッドのX/Y分割数
const int X_N = 64;
const int Y_N = 64;
// 座標値配列で、X/Y/Z座標を表すインデックス
const int X = 0;
const int Y = 1;
const int Z = 2;
// 頂点座標を格納する配列(最右次元は0=X,1=Y,2=Z)
float vertex[ Y_N ][ X_N ][ 3 ];
// 頂点のZ方向速度
float vertexVZ[ Y_N ][ X_N ] = 0.0;
// 頂点のZ方向の力
float vertexFZ[ Y_N ][ X_N ] = 0.0;
// 領域の辺の長さ
const float X_LENGTH = 4.0;
const float Y_LENGTH = 4.0;
// 単位面積あたりの質量密度
const float DENSITY = 10.0;
// 張力
const float TENSION = 3.0;
// 減衰力係数
const float FRICTION = 0.0;
// 初期パルスの幅
const float PULSE_WIDTH = 0.3;
// 初期パルスの高さ
const float PULSE_HEIGHT = 2.0;
// 自由端かどうか
const bool FREE_END = true;
/**
* 1フレームあたり、力学計算(時間発展)を行う回数です。
*
* 波を速くしたい場合、DTを荒くしたり、張力を上げると、
* 精度限界を超えて運動が発散してしまう場合があります。
* その回避策で、1フレーム内に細かいDTで繰り返し計算します。
*/
const int UPDATE_PER_FRAME = 3;
// シミュレーションの時間刻み
const float DT = 0.01;
// 格子点間距離(ポリゴンの辺の長さ)
const float DX = X_LENGTH / (X_N-1);
const float DY = Y_LENGTH / (Y_N-1);
// 波モデルを配置する座標系
int waveCoordinate;
// モデルのIDを格納する
int waveModel;
/* --------------------------------------------------
* ここから、初期化処理に関する部分
* (モデルの生成や初期形状設定など)
*/
/*
* ここはフレームワークから、
* プログラム起動後に1度だけコールされます。
*/
void onStart(int renderer){
// 波座標系を生成
initializeCoordinate();
// 波座標系を配置
mountCoordinate(waveCoordinate, renderer);
// 波モデルを生成して配置
initializeModel();
// 波モデルを波座標系に配置
mountModel(waveModel, renderer, waveCoordinate);
// 波モデルの初期形状をガウス波束で設定
setGaussianWave(PULSE_WIDTH, PULSE_HEIGHT);
}
/**
* 台座となる座標系を生成します。
*/
void initializeCoordinate(){
// 波モデルを配置する座標系を生成
waveCoordinate = newCoordinate();
// 原点を 領域長/2 だけ平行移動
moveCoordinate(
waveCoordinate,
-X_LENGTH/2.0, -Y_LENGTH/2.0, 0.0
);
// 角度を調整
rotCoordinate(waveCoordinate, -PI/4.0, 1.0, 0.0, 0.5);
}
/**
* モデルを生成します。
*/
void initializeModel(){
// 四角形グリッド形式で波のモデルを生成
waveModel = newModel(vertex, QUADRANGLE_GRID);
// 波モデルの色設定(赤、緑、青、α値)
setModelColor(waveModel, 0, 0, 255, 255);
// 裏面のカリング(描画省略)を無効化
setModelCull(waveModel, false, false);
// 描画を面にするかワイヤーにするか、ユーザーに選択を求める
bool fill = confirm(
"立体的な面による描画を行いますか ?"
+ EOL
+ "(「いいえ」でワイヤーによる描画 )"
);
// モデル構成ポリゴンのフィル設定(falseでワイヤー描画)
setModelFill(waveModel, fill);
}
/**
* 頂点配列をガウス波束の形状に設定します。
*/
void setGaussianWave(float width, float height){
for(int i=0; i<Y_N; i++){
for(int j=0; j<X_N; j++){
// 頂点のX/Y座標
float x = j * DX;
float y = i * DY;
// 中心から頂点までの距離の2乗
float r2 =
(x - X_LENGTH/2.0)*(x - X_LENGTH/2.0)
+ (y - Y_LENGTH/2.0)*(y - Y_LENGTH/2.0);
// 頂点のZ座標を、中心からの距離とガウス関数で計算
float z = height * exp( -r2 / (2*width*width) );
// 頂点配列に座標値をセット
vertex[i][j][X] = x;
vertex[i][j][Y] = y;
vertex[i][j][Z] = z;
}
}
}
/* --------------------------------------------------
* ここから、更新処理に関する部分
* (力学演算による形状の時間発展など)
*/
/*
* ここはフレームワークから、
* ここは1秒間に数十回、繰り返しコールされます。
*/
void onUpdate(int renderer){
// 質点1個あたりの質量
float m = DENSITY
* X_LENGTH * Y_LENGTH
/ ( (X_N+1) * (Y_N+1) );
// UPDATE_PER_FRAME回だけ繰り返し力学演算(時間発展)
for(int cycle=0; cycle<UPDATE_PER_FRAME; cycle++){
// 質点にはたらく力を計算
if(FREE_END){
updateForceFreeEnd();
}else{
updateForceFixedEnd();
}
// 位置と速度の計算
for(int i=0; i<Y_N; i++){
for(int j=0; j<X_N; j++){
// 頂点の速度変化の計算
vertexVZ[i][j] += vertexFZ[i][j] / m * DT;
// 頂点の座標変化の計算
vertex[i][j][Z] += vertexVZ[i][j] * DT;
}
}
// モデルの頂点配列を更新
setModelVertex(waveModel, vertex, QUADRANGLE_GRID);
}
}
/**
* 1個の隣接質点から受ける力を返します。引数 delta には DX または DY を指定します。
* (高速化目的でマクロ関数にしているため、実行前にインライン展開されます)
*/
macro getForce(float zSide, float zCenter, float tension, float delta){
return ( (zSide - zCenter) * tension / delta );
}
/**
* 固定端の場合、質点にはたらく力を計算します。
*/
void updateForceFixedEnd(){
float force;
// 端以外の場合のみ、質点にかかる力を計算する
for(int i=1; i<Y_N-1; i++){
for(int j=1; j<X_N-1; j++){
// バネからかかる力
force = 0.0;
// X方向に隣接する質点とのバネからかかる力
force += getForce(vertex[i][j+1][Z], vertex[i][j][Z], TENSION, DX);
force += getForce(vertex[i][j-1][Z], vertex[i][j][Z], TENSION, DX);
// Y方向に隣接する質点とのバネからかかる力
force += getForce(vertex[i+1][j][Z], vertex[i][j][Z], TENSION, DY);
force += getForce(vertex[i-1][j][Z], vertex[i][j][Z], TENSION, DY);
// バネからかかる力 + 減衰力 = 質点にかかる力
vertexFZ[i][j] = force - FRICTION * vertexVZ[i][j];
}
}
}
/**
* 自由端の場合、質点にはたらく力を計算します。
*/
void updateForceFreeEnd(){
float force;
// 質点にかかる力の計算
for(int i=0; i<Y_N; i++){
for(int j=0; j<X_N; j++){
// バネからかかる力
force = 0.0;
// X方向に隣接する質点とのバネからかかる力
if(j != 0){
force += getForce(vertex[i][j-1][Z], vertex[i][j][Z], TENSION, DX);
}
if(j != X_N-1){
force += getForce(vertex[i][j+1][Z], vertex[i][j][Z], TENSION, DX);
}
// Y方向に隣接する質点とのバネからかかる力
if(i != 0){
force += getForce(vertex[i-1][j][Z], vertex[i][j][Z], TENSION, DY);
}
if(i != Y_N-1){
force += getForce(vertex[i+1][j][Z], vertex[i][j][Z], TENSION, DY);
}
// バネからかかる力 + 減衰力 = 質点にかかる力
vertexFZ[i][j] = force - FRICTION * vertexVZ[i][j];
}
}
}
以下では、コードの各部について解説します。
先頭領域
まずはプログラムの先頭領域です。
coding UTF-8;
import Math;
import Graphics3D;
import graphics3d.Graphics3DFramework;
最初の行「 coding UTF-8; 」は、このプログラムのファイルが文字コード「 UTF-8 」を使用している事を明示しています。これは必須ではないのですが、書いておくと文字化け起因のトラブルを防げます。
続いて、import 文でライブラリを読み込んでいます。 この通り、まず標準ライブラリから、数学関数を扱う「 Math 」と、3次元グラフィックスを扱う標準ライブラリ「 Graphics3D 」を読み込んでいます。
加えて、3DCG用フレームワーク「 graphics3d.Graphics3DFramework 」も読み込んでいます。
グローバル変数の宣言
続いてグローバル変数の宣言です。
// グリッドのX/Y分割数
const int X_N = 64;
const int Y_N = 64;
// 座標値配列で、X/Y/Z座標を表すインデックス
const int X = 0;
const int Y = 1;
const int Z = 2;
// 頂点座標を格納する配列(最右次元は0=X,1=Y,2=Z)
float vertex[ Y_N ][ X_N ][ 3 ];
// 頂点のZ方向速度
float vertexVZ[ Y_N ][ X_N ] = 0.0;
// 頂点のZ方向の力
float vertexFZ[ Y_N ][ X_N ] = 0.0;
// 領域の辺の長さ
const float X_LENGTH = 4.0;
const float Y_LENGTH = 4.0;
// 単位面積あたりの質量密度
const float DENSITY = 10.0;
// 張力
const float TENSION = 3.0;
// 減衰力係数
const float FRICTION = 0.0;
// 初期パルスの幅
const float PULSE_WIDTH = 0.3;
// 初期パルスの高さ
const float PULSE_HEIGHT = 2.0;
// 自由端かどうか
const bool FREE_END = true;
/**
* 1フレームあたり、力学計算(時間発展)を行う回数です。
*
* 波を速くしたい場合、DTを荒くしたり、張力を上げると、
* 精度限界を超えて運動が発散してしまう場合があります。
* その回避策で、1フレーム内に細かいDTで繰り返し計算します。
*/
const int UPDATE_PER_FRAME = 3;
// シミュレーションの時間刻み
const float DT = 0.01;
// 格子点間距離(ポリゴンの辺の長さ)
const float DX = X_LENGTH / (X_N-1);
const float DY = Y_LENGTH / (Y_N-1);
// 波モデルを配置する座標系
int waveCoordinate;
// モデルのIDを格納する
int waveModel;
前半部では、頂点配列や、速度、加速度の配列など、基盤としての変数を宣言しています。
続く中盤部では、張力や質量密度など、力学モデルのパラメータ変数を宣言しています。
最後に、描画モデルや座標系のIDを格納する変数など、グローバルに必要な雑用変数を宣言しています。
初期化処理を行う onStart関数
続いて具体的な処理を見ていきましょう。まずは プログラムの準備的な処理 = 初期化処理 を行うonStart関数です。
この関数は、プログラム開始後に一度だけ、フレームワークから自動でコールされる仕組みになっています。
/*
* ここはフレームワークから、
* プログラム起動後に1度だけコールされます。
*/
void onStart(int renderer){
// 波座標系を生成
initializeCoordinate();
// 波座標系を配置
mountCoordinate(waveCoordinate, renderer);
// 波モデルを生成して配置
initializeModel();
// 波モデルを波座標系に配置
mountModel(waveModel, renderer, waveCoordinate);
// 波モデルの初期形状をガウス波束で設定
setGaussianWave(PULSE_WIDTH, PULSE_HEIGHT);
}
前半部では座標系の準備を行い、後半部ではモデルの準備を行っています。
座標系は、モデルを配置する台座のような存在です。デフォルトでもワールド座標系という特別な座標系が最初から用意されていますが、そこに配置すると、座標(0, 0, 0)の点が画面の中心に描かれてしまいます。 それだと、今回のモデルだとメッシュの端が画面中心に来てしまいます。 やはりモデルの中心を画面中心に一致させたいので、別に座標系を一つ用意し、その上にモデルを配置しています。
具体的な座標系の生成や位置設定などは、後述するinitializeCoordinate関数に実装しているので、ここではそれをコールしています。すると、グローバル座標系の waveCoordinate に、生成した座標系のIDが格納されます。 それをGraphics3Dライブラリの addCoordinate 関数でレンダラー(描画エンジン)に登録しています。なお、この時点で座標系はワールド座標系上に配置されます。
続いてモデルの生成ですが、これも後述するinitializeModel関数に実装しているので、ここではそれをコールしています。すると、グローバル座標系の waveModel に、生成したモデルのIDが格納されます。 それをGraphics3Dライブラリの addModel 関数で、レンダラー(描画エンジン)に登録すると共に、先ほど確保した座標系上に配置しています。
最後に、後述する setGaussianWave 関数をコールし、頂点配列が格納する座標値を、ガウス波束の形状となるように初期設定しています。
以上がinitialize関数の中身であり、初期化処理の大まかな流れをまとめた形となっています。 ここからは、initialize関数でコールしていた関数の中身を、具体的に見ていきます。
座標系の初期化 - initializeCoordinate関数
まずは座標系の生成と位置設定を行うinitializeCoordinate関数です。
/**
* 台座となる座標系を生成します。
*/
void initializeCoordinate(){
// 波モデルを配置する座標系を生成
waveCoordinate = newCoordinate();
// 原点を 領域長/2 だけ平行移動
moveCoordinate(
waveCoordinate,
-X_LENGTH/2.0, -Y_LENGTH/2.0, 0.0
);
// 角度を調整
rotZCoordinate(waveCoordinate, PI/3.0);
rotXCoordinate(waveCoordinate, -PI/4.0);
}
内容は、まず座標系を生成し、moveCoordinate関数でメッシュ全長の半分だけ平行移動させています。これにより、この座標系をワールド座標系上に配置した際、メッシュの中心が画面中心に一致するようになります。
加えて、rotZCoordinate / rotXCoordinate関数で角度を微妙に変えています。これで、プログラム開始時に、斜め見下ろし視点で見たような感じになります。
モデルの初期化 - initializeModel関数
続いて、モデルの生成と各種設定を行うinitializeModel関数です。
/**
* モデルを生成します。
*/
void initializeModel(){
// 四角形グリッド形式で波のモデルを生成
waveModel = newModel(vertex, QUADRANGLE_GRID);
// 波モデルの色設定(赤、緑、青、α値)
setModelColor(waveModel, 0, 0, 255, 255);
// 裏面のカリング(描画省略)を無効化
setModelCull(waveModel, false, false);
// 描画を面にするかワイヤーにするか、ユーザーに選択を求める
bool fill = confirm(
"立体的な面による描画を行いますか ?"
+ lf()
+ "(「いいえ」でワイヤーによる描画 )"
);
// モデル構成ポリゴンのフィル設定(falseでワイヤー描画)
setModelFill(waveModel, fill);
}
最初の newModel 関数で、格子メッシュの頂点配列から、モデルを生成しています。QUADRANGLE_GRIDという引数は、Graphics3Dライブラリに定義された定数で、頂点配列が四角形格子メッシュ形式である事を指定します。
続いて、色設定やカリング(描画省略)設定、フィル(塗りつぶし)設定などを行っています。
頂点配列の初期化 - setGaussianWave関数
初期化処理の最後にコールされていたのが、setGaussianWave関数です。
/**
* 頂点配列をガウス波束の形状に設定します。
*/
void setGaussianWave(float width, float height){
for(int i=0; i<Y_N; i++){
for(int j=0; j<X_N; j++){
// 頂点のX/Y座標
float x = j * DX;
float y = i * DY;
// 中心から頂点までの距離の2乗
float r2 =
(x - X_LENGTH/2.0)*(x - X_LENGTH/2.0)
+ (y - Y_LENGTH/2.0)*(y - Y_LENGTH/2.0);
// 頂点のZ座標を、中心からの距離とガウス関数で計算
float z = height * exp( -r2 / (2*width*width) );
// 頂点配列に座標値をセット
vertex[i][j][X] = x;
vertex[i][j][Y] = y;
vertex[i][j][Z] = z;
}
}
}
この関数は、頂点配列の座標値を、メッシュ中心からの距離を用いたガウス波束で初期設定する内容となっています。
ガウス波束とは、断面がガウス関数:
\( f(x) = \exp{ (x-m)^2 / 2 \sigma^2 } \)となる波束で、滑らかな山のような形をしています。上式で m は山のピークの位置に一致し、σは山のおおまかな幅に一致します。
今回は、このガウス関数に、メッシュ中心からの2次元的な距離を用いる事で、円形の山の形を作っています。
更新処理を行う onUpdate関数
初期化処理は以上です。続いていよいよ、力学計算による変形などを行う、更新処理の内容を見ていきましょう。
更新処理の大まかな流れは、onUpdate関数に実装しています。
この関数は、プログラム開始から終了するまでの間、一秒間に数十回(設定可能)の割合、フレームワークから繰り返し呼ば続けるという仕組みになっています。画面更新タイミングの間に呼ばれるため、ここでモデルを少しずつ変形させる事で、アニメーションの原理で画面を滑らかに動かす事ができるというわけです。
onUpdate関数の内容は、以下のようになっています。
/*
* ここはフレームワークから、
* ここは1秒間に数十回、繰り返しコールされます。
*/
void onUpdate(int renderer){
// 質点1個あたりの質量
float m = DENSITY
* X_LENGTH * Y_LENGTH
/ ( (X_N+1) * (Y_N+1) );
// UPDATE_PER_FRAME回だけ繰り返し力学演算(時間発展)
for(int cycle=0; cycle<UPDATE_PER_FRAME; cycle++){
// 質点にはたらく力を計算
if(FREE_END){
updateForceFreeEnd();
}else{
updateForceFixedEnd();
}
// 位置と速度の計算
for(int i=0; i<Y_N; i++){
for(int j=0; j<X_N; j++){
// 頂点の速度変化の計算
vertexVZ[i][j] += vertexFZ[i][j] / m * DT;
// 頂点の座標変化の計算
vertex[i][j][Z] += vertexVZ[i][j] * DT;
}
}
// モデルの頂点配列を更新
setModelVertex(waveModel, QUADRANGLE_GRID, vertex);
}
}
先頭では、単位面積あたりの質量密度 DENSITY から、質点1個あたりの質量 m を求めています。グローバルに置いても良いのですが、大した計算コストでも無いので可読性優先でローカルに求めています。
その下は for (int cycle=0; cycle< UPDATE_PER_FRAME; cycle++) というループで囲われています。これにより、update関数の中身を、一回コールあたり複数回実行するような形になっています。 update関数は1フレーム(画面更新)ごとに呼ばれるため、これはつまるところ、 画面を一枚描くごとに、複数回の力学演算を行う という事になります。これは、シミュレーションの大体の進行速度を調整するためです。
ループ内では、題材解説で詳しく述べたアルゴリズム通り、質点にかかる力を計算し、そして数値積分によって質点の速度と位置座標を計算しています。
最後に、setModelVertex 関数で、新しい位置座標が格納されている頂点配列を、モデルに再設定しています。これでモデルが少し変形します。
ここまでが、更新処理の大まかな流れになっています。
隣接質点から受ける力の計算 - getForce関数
それでは、具体的に更新処理の詳細な処理内容を見ていきましょう。
まずは質点が、それに隣接する1個の質点から受ける力を求める、getForce関数です。
/**
* 1個の隣接質点から受ける力を返します。
* 引数 delta には DX または DY を指定します。
* (高速化目的でマクロ関数にしているためインライン展開されます)
*/
macro getForce(float zSide, float zCenter, float tension, float delta){
return ( (zSide - zCenter) * tension / delta );
}
ここで関数の型宣言部が「 macro 」となっていますが、これはマクロ関数である事を意味します。マクロ関数では、プログラムの読み込み時に、その内容がコール部分にインライン展開されます。これにより、関数コールのオーバーヘッドを回避する事が可能です。
つまりは、マクロ関数の方が、通常の関数よりもコールが軽いという事になります。しかし、エラーメッセージが分かり辛くなる事や、一行の処理しか記述できないなどのデメリットもあります。
今回、このgetForce関数は、後述するupdateForce系 関数内において、2重のforループの中でコールされるので、オーバーヘッドはかなり効いてきます。そのため、デメリットを考慮した上で使用しています。
全質点にかかる力を計算(固定端) - updateForceFixedEnd関数
続いて、上述のgetForce関数を使用し、全質点にかかる力を計算する処理です。
これには固定端と自由端の2通りを実装していますが、まずは簡単な固定端を扱うupdateForceFixedEnd関数を見てみましょう。
/**
* 固定端の場合、質点にはたらく力を計算します。
*/
void updateForceFixedEnd(){
float force;
// 端以外の場合のみ、質点にかかる力を計算する
for(int i=1; i<Y_N-1; i++){
for(int j=1; j<X_N-1; j++){
// バネからかかる力
force = 0.0;
// X方向に隣接する質点とのバネからかかる力
force += getForce(vertex[i][j+1][Z], vertex[i][j][Z], TENSION, DX);
force += getForce(vertex[i][j-1][Z], vertex[i][j][Z], TENSION, DX);
// Y方向に隣接する質点とのバネからかかる力
force += getForce(vertex[i+1][j][Z], vertex[i][j][Z], TENSION, DY);
force += getForce(vertex[i-1][j][Z], vertex[i][j][Z], TENSION, DY);
// バネからかかる力 + 減衰力 = 質点にかかる力
vertexFZ[i][j] = force - FRICTION * vertexVZ[i][j];
}
}
}
この通り、端(辺上)を除く全ての質点について、前後左右で4個の質点とのバネから受ける力を合計し、それに減衰力を加えて求めています。
固定端では力は常に 0(初期値)であるため、端(辺上)の質点については何もしていません。
この通り、固定端だとシンプルな処理になります。
全質点にかかる力を計算(自由端) - updateForceFreeEnd関数
今度は、自由端を扱うupdateForceFreeEnd関数を見てみましょう。今度は少し複雑です。
/**
* 自由端の場合、質点にはたらく力を計算します。
*/
void updateForceFreeEnd(){
float force;
// 質点にかかる力の計算
for(int i=0; i<Y_N; i++){
for(int j=0; j<X_N; j++){
// バネからかかる力
force = 0.0;
// X方向に隣接する質点とのバネからかかる力
if(j != 0){
force += getForce(vertex[i][j-1][Z], vertex[i][j][Z], TENSION, DX);
}
if(j != X_N-1){
force += getForce(vertex[i][j+1][Z], vertex[i][j][Z], TENSION, DX);
}
// Y方向に隣接する質点とのバネからかかる力
if(i != 0){
force += getForce(vertex[i-1][j][Z], vertex[i][j][Z], TENSION, DY);
}
if(i != Y_N-1){
force += getForce(vertex[i+1][j][Z], vertex[i][j][Z], TENSION, DY);
}
// バネからかかる力 + 減衰力 = 質点にかかる力
vertexFZ[i][j] = force - FRICTION * vertexVZ[i][j];
}
}
}
この通り、前後左右の力の和を取っていく過程で、if による分岐が追加されています。そして、for ループも、端(辺上)の点を含むものになっています。
この処理では、端(辺上)を含むあらゆる質点についてなぞっていき、毎回、その位置の前後左右にバネがあるか(端かどうか)を分岐で判定しています。
分岐によって、その方向にバネがあると分かれば、そのバネから受ける力を加算しています。これにより、端では自然と3個(返上)または2個(カド)のバネから受ける力のみが合計されるようになり、自由端の処理が実現できます。
ライセンス
このVCSSL/Vnanoコード( 拡張子が「.vcssl」や「.vnano」のファイル )は実質的な著作権フリー(パブリックドメイン) である CC0 の状態で公開しています※。 記事中にC言語/C++/Java言語などでのサンプルコードが掲載されいてる場合は、それらについても同様です。 そのままでのご利用はもちろん、改造や流用などもご自由に行ってください。
※ ただし、このコードの配布フォルダ内には、ダウンロード後すぐに実行できるように、 VCSSLの実行環境も同梱されており、そのライセンス文書は「 License 」フォルダ内に同梱されています (要約すると、商用・非商用問わず自由に使用できますが、使用の結果に対して開発元は一切の責任を負いません、といった具合の内容です)。 配布フォルダ内の各構成物の一覧やライセンスについては「 ReadMe_使用方法_必ずお読みください.txt 」をご参照ください。
※ Vnano の実行環境については、別途スクリプトエンジンのソースコードも一般公開しており、 何らかのソフトウェア内に組み込んでご利用いただく事も可能です。詳細はこちらをご参照ください。
この記事中の商標などについて
- OracleとJavaは、Oracle Corporation 及びその子会社、関連会社の米国及びその他の国における登録商標です。文中の社名、商品名等は各社の商標または登録商標である場合があります。
- Windows は、米国 Microsoft Corporation の米国およびその他の国における登録商標です。この記事は独立著作物であり、Microsoft Corporation と関連のある、もしくはスポンサーを受けるものではありません。
- Linux は、Linus Torvalds 氏の米国およびその他の国における商標または登録商標です。
- その他、文中に使用されている商標は、その商標を保持する各社の各国における商標または登録商標です。
|
Vnano版 | ローレンツ方程式を数値的に解くプログラム |
|
|
|
ローレンツ方程式を4次ルンゲ=クッタ法によって解き、グラフ描画用のデータを出力するプログラムです。 |
|
波の干渉(面上の円形波)のアニメーション表示 |
|
|
|
面上の円形波が干渉する様子を、パラメータを操作しながらアニメーションで見られるプログラムです。 |
|
円形波のアニメーション表示 |
|
|
|
振幅・波長・周期をスライダ―で操作しながら、円形波のグラフをアニメーションで見られるプログラムです。 |
|
波の干渉(線上の正弦波)のアニメーション表示 |
|
|
|
線上(1次元の)の正弦波が干渉する様子を、パラメータを操作しながらアニメーションで見られるプログラムです。 |
|
正弦波のアニメーション表示 |
|
|
|
振幅・波長・周期をスライダ―で操作しながら、正弦波のグラフをアニメーションで見られるプログラムです。 |
|
凹レンズを通過する波のシミュレーション |
|
|
|
凹レンズ形状の高密度媒質を通過する、波のシミュレーションです。 |
|
凸レンズを通過する波のシミュレーション |
|
|
|
凸レンズ形状の高密度媒質を通過する、波のシミュレーションです。 |
|
乱雑な密度分布における波のシミュレーション |
|
|
|
密度分布が乱雑な媒質中における、波の伝播のシミュレーションです。 |
|
ローレンツアトラクタ(ファイル出力版) |
|
|
|
4次精度ルンゲ=クッタ法により、ローレンツアトラクタを求めるプログラムです。 |
|
波の屈折のシミュレーション |
|
|
|
密度の異なる領域を、波が屈折しながら通過するシミュレーションです。 |
|
力学アルゴリズムによる波のシミュレーション(面上の波) |
|
|
|
媒質をバネと格子点で近似し、力学的なアルゴリズムで動かす事による、波のシミュレーションです。 |
|
手動で波を発生させるシミュレーション |
|
|
|
スライダーをマウスで動かす事により、波を発生させるシミュレーションです。 |
|
力学アルゴリズムによる波のシミュレーション(線上の波) |
|
|
|
媒質をバネと格子点で近似し、力学的なアルゴリズムで動かす事による、波のシミュレーションです。 |
|
二重振り子のシミュレーション |
|
|
|
ラグランジュ方程式を用いた、二重振り子のシミュレーションです。 |
|
ローレンツアトラクタ(GUI版) |
|
|
|
4次精度ルンゲ=クッタ法により、ローレンツアトラクタを求めるプログラムです。 |