凸レンズを通過する波のシミュレーション

このVCSSLプログラムは、凸レンズ形状をした高密度媒質を、波が通過する様子をシミュレーションします。 レンズ通過時に波が屈折し、焦点に集まる様子を、アニメーションで見る事ができます。

スポンサーリンク

---

使用方法

ダウンロードと展開（解凍）

まず、PC（スマホは未対応）で上の画面の「 ダウンロード 」ボタンを押してください。 するとZIP形式で圧縮されたファイルがダウンロードされます。

その後、ZIPファイルを右クリックして「すべて展開」や「ここに展開」などで展開（解凍）してください。 展開が成功すると、ZIPファイルと同じ名前のフォルダができ、その中にZIPファイルの中身が入っています。

» 展開がエラーで止まってしまう場合や、ファイル名が文字化けしてしまう場合は…

プログラムの起動

Windows をご使用の場合

上記でZIPファイルを展開したフォルダ内にある、以下のバッチファイルをダブルクリック実行してください：

もしプログラムを書き変えながら使いたい場合は、代わりに「 VCSSL_Editor__プログラム編集はこちら.bat 」を実行してください。

正常に起動できると、初回のみ、Java実行環境を入手するか等を尋ねられるので、適時答えて済ませると、プログラムが起動します。 2回目以降はすぐに起動します。

» うまく起動できずにエラーになってしまう場合は…

Linux 等をご使用の場合

ZIPファイルを展開したフォルダ内へコマンドライン端末で cd して、以下の通り入力して実行してください：

» javaコマンドが使用できない等のエラーが表示される場合は…

起動後の操作方法

起動すると、ウィンドウ上に画面が表示され、波が凸レンズ状の高密度媒質を通過する様子がアニメーションで見られます。

画面ウィンドウ上では、下記のマウス操作を行えます。

• 左ドラッグ … 視点の回転
• 右ドラッグ … 視点の平行移動
• ホイールスクロール … 拡大/縮小

密度分布の変更

密度分布は、画像ファイル「 density.png 」 として描いたものを読み込むようになっています。 実際にこのシミュレーションで用いているのは以下の画像です：

この通り、凸レンズ状の形状が描かれています。この画像ファイルの内容を描きかえる事により、 自由な密度分布に設定できます。 画像ファイルのピクセルごとの明るさが、その点の媒質密度に対応します。 具体的には、暗いほど密度が重く、明るいほど軽くなります。

パラメータの変更

波に関する各種パラメータは、プログラムのコードの先頭領域にまとめて記載されています。 それらの値を書き換えると、色々と条件を変えてシミュレーションを楽しめます。

シミュレーションの題材解説

このプログラムでは、凸レンズ形状の媒質を、波が通過する様子をシミュレーションしています。 ここでは、その際に生じる現象について、物理学的な観点から、簡単に考察してみましょう。

凸レンズ形状の密度分布

上でも述べましたが、このシミュレーションで用いた媒質の密度分布は、 以下のPNG形式画像ファイルとして読み込んでいます。

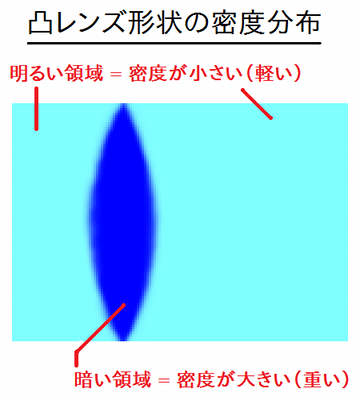
上記の図の、ピクセルごとの明度情報が、その点の密度分布に対応します。 暗い部分ほど密度が重く、明るい部分ほど軽くなります。

上図の通り、このシミュレーションの媒質は、低密度の媒質中に、 凸レンズ形状の高密度領域が埋め込まれた密度分布となっています。

媒質密度と波の速さ

このシミュレーションにおいて重要なのは、媒質密度と、波の速さとの関係です。

波は、密度の大きい（重い）媒質中では遅く、 逆に密度の小さい（軽い）媒質中では速く伝わるという、非常に重要な性質があります。 実は波の屈折現象は、この性質に起因するものです。逆に言えば、 この性質さえ覚えておけば、レンズにおける屈折現象なども、直感的に理解する事ができます。

このあたりについては、以下のシミュレーションで分かりやすく見る事ができます。ぜひ合わせてご参照下さい。

• 波の屈折のシミュレーション

光でも「密度」を「屈折率」に置き換えて解釈すれば同様

今回のシミュレーションでは、電磁気的な波である「 光 」では無く、 力学的な波（つまりは弾性体の振動）を扱っています。

しかし、光の場合でも、媒質密度を 屈折率 に置き換えれば、ほぼ同様の議論を行う事ができます。

光の場合は、屈折率が高いほど、遅く進みます。 つまり、よく言われる「光の速さ」は真空中のもので、ガラスの中などではそれよりも遅く進むのです。 これは、媒質密度が高いほど、力学的な波が遅く進むのと同じ対応関係です。

そのため、光学的なレンズに対しては、今回のシミュレーションにおけるレンズの高密度領域を、 単に高屈折率の領域と見なせば、同様の解釈が可能です。

シミュレーション結果

それではシミュレーションの結果を見てみましょう。

実際に、このシミュレーションを実行した様子が下図です。

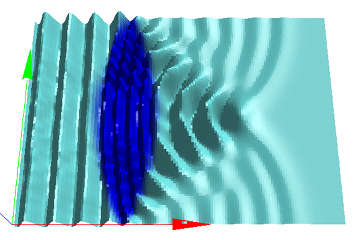
上図において、波は左から右へまっすぐ入射しています。波が進行する向きと速さを、矢印で表したのが下図です。

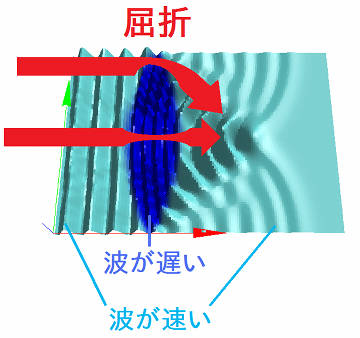
上図において、矢印の太さが波の速さ、矢印の向きが波の進行方向に対応しています。

レンズ内は密度が高いため、波の進む速さが遅くなります。 そしてレンズ中央部以外は、波の進行方向に対して境界に角度が付いているため、 先にレンズに触れた中心側の波が遅れ、外側の波はそれを追い越すように回り込み、 波の進行方向が屈折します。

さらに、レンズ中央部は厚く、端部は薄くなっているため、中央部よりも端部のほうが、 通過時に早いタイミングでレンズを脱出します。 端部の波がレンズを脱出しても、中央部の波はまだ（進むのが遅い）レンズ内に取り残されているため、 ここでも回り込むように波の屈折が生じます。

このようにして、最初はまっすぐに入射してきた波が、レンズに進入・脱出する際に屈折し、 通過後に一点に収束するような方向に進みます。 この収束点は一般に「 焦点 」と呼ばれます。

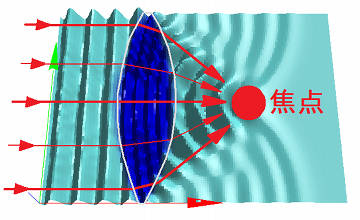
なお、ここで「 何故、凸レンズでは一点に集中するように屈折するのか ? 」 という疑問が生じるかもしれません。

この疑問はもっともです。実は波が焦点に集中するのは自然の法則でも何でもなく、 単に凸レンズをそのような形に製造しているだけです。 そして、そのように製造する理由も、単純に「 便利だから 」です。

つまり、適当に凸形状を作っておけば、波や光は一点に集中するという訳では決してありません。 それどころか、精度良く波や光を一点に収束させる、 つまり高精度な焦点を実現するには、高度な技術と複雑な理論が必要です。

さて、波の先端が焦点に収束した後、波はどう進むのでしょうか。もう少し後の時間まで見てみましょう。 すると以下の図のようになります。

このように、収束して焦点を通過した波は、今度は逆に、拡散するように進みます。

上図では、上下の境界部分での反射波などが影響して、少し見辛くなっていますので、 波の腹の部分を赤い線で強調してみましょう。

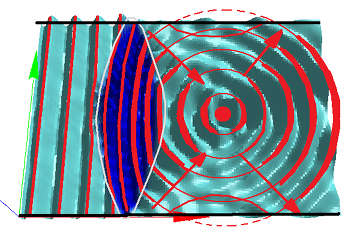
この通り、焦点に向かって収束した波は、その後拡散していく際も、焦点を中心として進む様子が見て取れます。

ここまでをまとめて図にすると、凸レンズを通過する波の進み方は、以下のようになります。

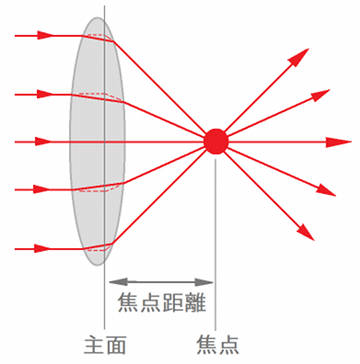
上図の通り、「凸レンズに対してまっすぐ入射してきた波は、全て焦点に収束し、 その後は焦点から放射状に拡散する」、とまとめる事ができます。 この事が、凸レンズのもっとも重要な性質です。

ところで、実際には凸レンズを通過する波は、レンズ表面で二回屈折するわけですが、 レンズ内のある面（線）で一回だけ屈折するとみなすと（上図の補助線）、扱いが簡単になります。 この面は一般に主面と呼ばれます。 そして、主面から焦点までの距離は 焦点距離 と呼ばれます。

例を挙げると、カメラのレンズは簡単に言えば凸レンズと見なす事ができますが（ 実際には収差を消すため、多くのレンズが組み合わさっています ）、広角レンズやマクロレンズの焦点距離は短く、望遠レンズの焦点距離は長いものとなっています。

---

スポンサーリンク

---

コード解説

このプログラムのコードは、プログラミング言語VCSSLで記述されています。

実は、コード内容は以下のページのプログラムと全く同じで、 密度分布を設定する画像ファイル（ density.png ）が異なるだけです。 モデルやシミュレーション方法、コードなどについての詳しい解説は、以下のページをご参照下さい。

• 波の屈折のシミュレーション

ここでは、コード全体のみを掲載しておきます。

ライセンス

このVCSSL/Vnanoコード（ 拡張子が「.vcssl」や「.vnano」のファイル ）は実質的な著作権フリー（パブリックドメイン) である CC0 の状態で公開しています※。 記事中にC言語/C++/Java言語などでのサンプルコードが掲載されいてる場合は、それらについても同様です。 そのままでのご利用はもちろん、改造や流用などもご自由に行ってください。

※ ただし、このコードの配布フォルダ内には、ダウンロード後すぐに実行できるように、 VCSSLの実行環境も同梱されており、そのライセンス文書は「 License 」フォルダ内に同梱されています （要約すると、商用・非商用問わず自由に使用できますが、使用の結果に対して開発元は一切の責任を負いません、といった具合の内容です）。 配布フォルダ内の各構成物の一覧やライセンスについては「 ReadMe_使用方法_必ずお読みください.txt 」をご参照ください。

※ Vnano の実行環境については、別途スクリプトエンジンのソースコードも一般公開しており、 何らかのソフトウェア内に組み込んでご利用いただく事も可能です。詳細はこちらをご参照ください。

この記事中の商標などについて

• OracleとJavaは、Oracle Corporation 及びその子会社、関連会社の米国及びその他の国における登録商標です。文中の社名、商品名等は各社の商標または登録商標である場合があります。
• Windows は、米国 Microsoft Corporation の米国およびその他の国における登録商標です。この記事は独立著作物であり、Microsoft Corporation と関連のある、もしくはスポンサーを受けるものではありません。
• Linux は、Linus Torvalds 氏の米国およびその他の国における商標または登録商標です。
• その他、文中に使用されている商標は、その商標を保持する各社の各国における商標または登録商標です。