» 詳しい使用方法や、エラーで展開できない際の対応方法などはこちら
波の干渉(面上の円形波)のアニメーション表示
面上の(2次元の)円形波が干渉する様子を再現する、VCSSL製の簡易シミュレーターです。
前回は単体の円形波のアニメーションを扱いましたが、今回はその続きです。 そもそも円形波とは? という場合は、まずは前回の内容をご参照ください。 今回は前回の続きとして、円形波を2つ重ね合わせて、干渉する様子をアニメーション表示してみましょう。
[ 関連記事 ]
- 前回: 円形波のアニメーション表示
- 前々回: 波の干渉(線上の正弦波)のアニメーション表示
使用方法
ダウンロードと展開(解凍)
まず、PC(スマホは未対応)で上の画面の「 ダウンロード 」ボタンを押してください。 するとZIP形式で圧縮されたファイルがダウンロードされます。
その後、ZIPファイルを右クリックして「すべて展開」や「ここに展開」などで展開(解凍)してください。 展開が成功すると、ZIPファイルと同じ名前のフォルダができ、その中にZIPファイルの中身が入っています。
» 展開がエラーで止まってしまう場合や、ファイル名が文字化けしてしまう場合は…
プログラムの起動
Windows をご使用の場合
上記でZIPファイルを展開したフォルダ内にある、以下のバッチファイルをダブルクリック実行してください:
もしプログラムを書き変えながら使いたい場合は、代わりに「 VCSSL_Editor__プログラム編集はこちら.bat 」を実行してください。
正常に起動できると、初回のみ、Java実行環境を入手するか等を尋ねられるので、適時答えて済ませると、プログラムが起動します。 2回目以降はすぐに起動します。
Linux 等をご使用の場合
ZIPファイルを展開したフォルダ内へコマンドライン端末で cd して、以下の通り入力して実行してください:
(プログラムの内容を書き変えながら使いたい場合は、代わりに VCSSL_Editor.jar を実行)
» javaコマンドが使用できない等のエラーが表示される場合は…
起動後の画面
起動すると、まず波のパラメータを数値入力するか尋ねられます。 特に「ぴったりこの値の波長にしたい」などの必要が無ければ、「いいえ」でスキップして構いません。
その後、波が3Dアニメーションで表示される画面が立ち上がります。
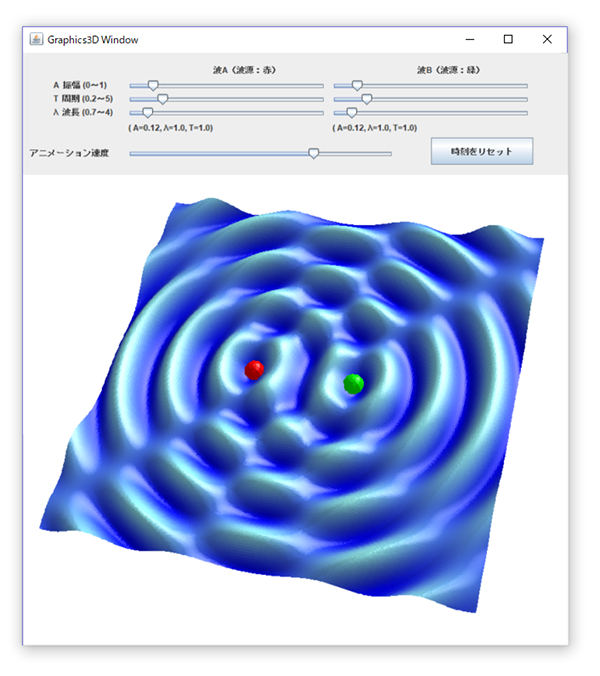
画面上部にあるスライダーで、波の波長や振幅、周期などのパラメータを自由に調整できます。
ウィンドウを閉じると、プログラムの実行が終了します。
波の面のなめらかさは、メッシュの刻み数 N の設定値によって変わります。 刻み数 N の値を変えるには、プログラムの本体「 InterferingCircularWave.vcssl 」をテキストエディタで開いて、 20 行目付近に「 const int N = 100; 」などと記述されている行の、右辺の値を書き換えてください。 N の値を大きくするほど、波の面はなめらかになりますが、処理が重くなります。
なお、書き換える際に、右辺の数値の右にある「 ; (セミコロン)」記号を消さないようにご注意ください。
題材解説
複数の異なる波を重ね合わせると、元のどちらの波とも違った形(と動き)をする波ができます。これを干渉といいます。
前々回では、X軸上で2つの正弦波が干渉する様子を扱いましたが、確かに合成波は、元の正弦波のどちらとも異なる、独特のパターンの形や動きをしていましたね。
今回は、そこから次元が1つ増えて、面の上を伝わる円形波を2つ重ね合わせて、干渉させてみましょう。 これもまた、独特のパターンや動きが見られて面白いですよ!
まずは、重ね合わせる2つの円形波、波Aと波Bの形や動きをそれぞれ確認
さて、まずは重ね合わせる2つの円形波(波A、波Bと呼びます)を、それぞれ単体で見てみましょう。 画面の一番上にあるスライダーで、波Bの振幅をゼロ(左端)にもっていくと、以下のように波Bが消えて波Aだけが見られます:
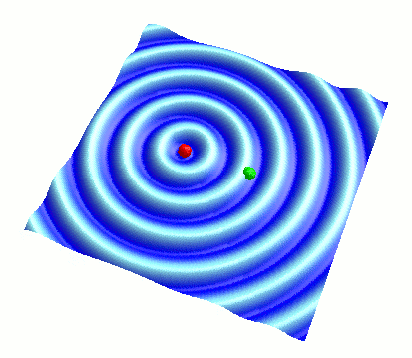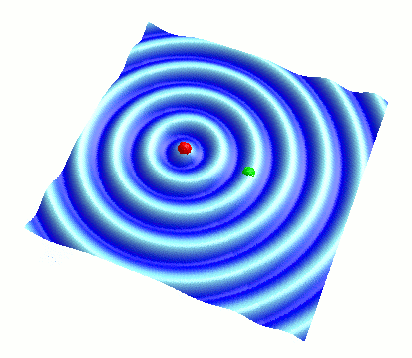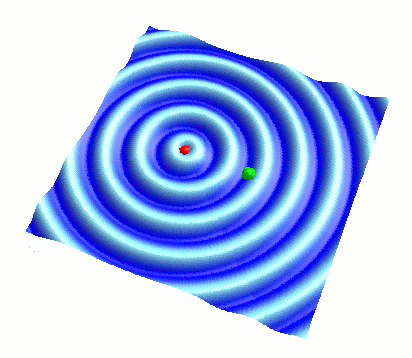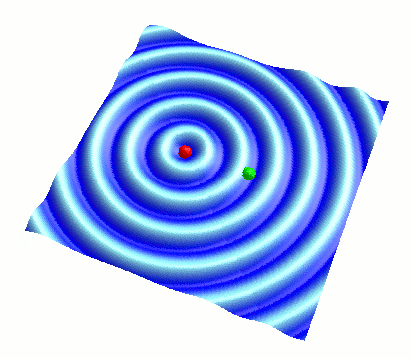
( 波Bの振幅を 0 にし、波Aだけを表示した様子 )
このように、上下に揺れる赤色のボールを波源として、そこから波が同心円状に広がっていきます。 これが、今回重ね合わせる円形波の形です。 この円形波は、波源を含む断面が正弦波になっています。 詳細は前回の記事をご参照ください:
- 前回: 円形波のアニメーション表示
さて、今度は波Bの振幅をゼロでない値に戻して、逆に波Aの振幅をゼロにもっていきましょう。 そうすると、以下のように波Aが消えて波Bだけが見られます:
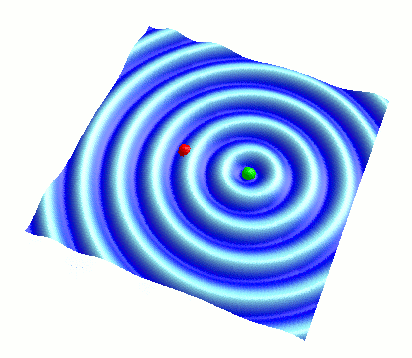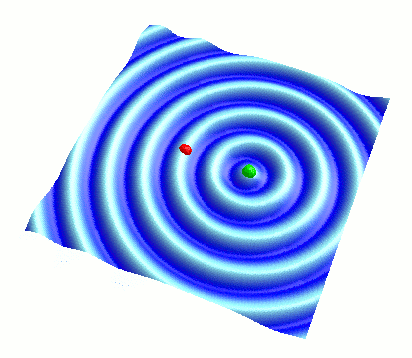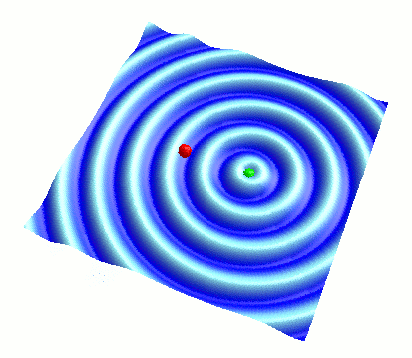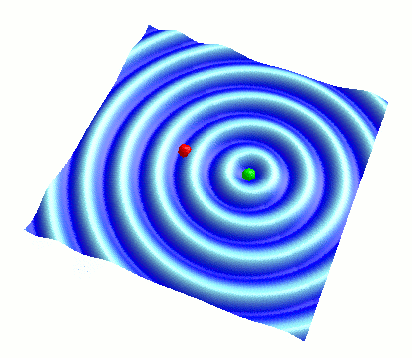
( 波Aの振幅を 0 にし、波Bだけを表示した様子 )
このように、今度は緑色のボールを波源として、そこから円形波が広がっていきます。
波長や周期は、スライダーを操作して変更しない限り、波Aと波Bで同じに設定してあります。 つまるところ、少し離れた赤色と緑色のボールを波源として、そこから全く同じ円形波が出て、広がっていっているわけですね。
波Aと波Bを、同程度の振幅で重ね合わせて干渉させると…
それでは、上で見た波Aと波Bを重ね合わせて、干渉させてみましょう。 波Aと波Bの振幅を同程度にそろえると、うまく独特のパターンを見られます。
…といっても、このプログラムを起動した時点で、ちょうどいいパターンが見られる状態になるようにしてあるので、起動後のデフォルト状態をそのまま観察すればOKです。すると、以下のような結果が得られます:
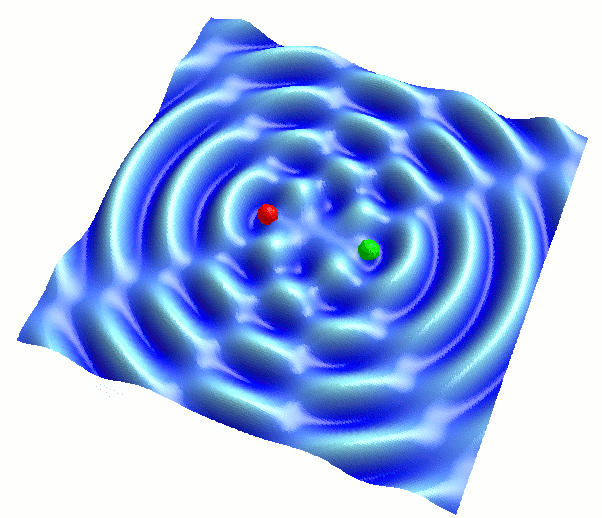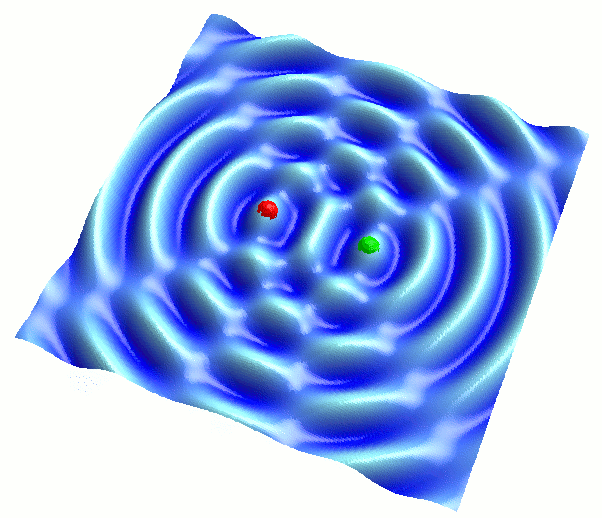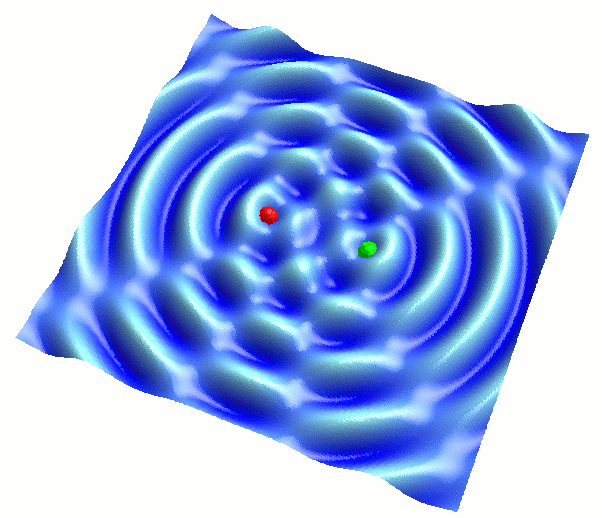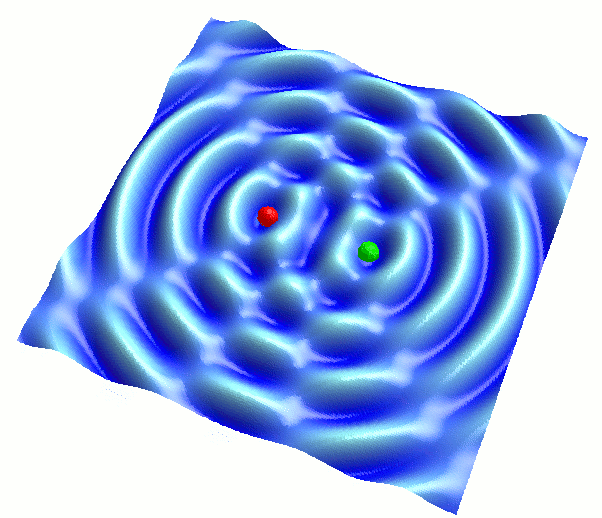
( 波Aと波Bの振幅をちょうど同程度にして、干渉させた様子。波長や振幅は同じ値です。うまく振幅を合わせられない場合は、プログラムを再起動すると、ちょうどこの図のセッティングになります。 )
なんともおかしなパターンですね。このパターンに注目するために、波長をもう少し短くして形を密にし、さらに真上から見下ろした様子を、アニメーションではなく静止画で見てみましょう:
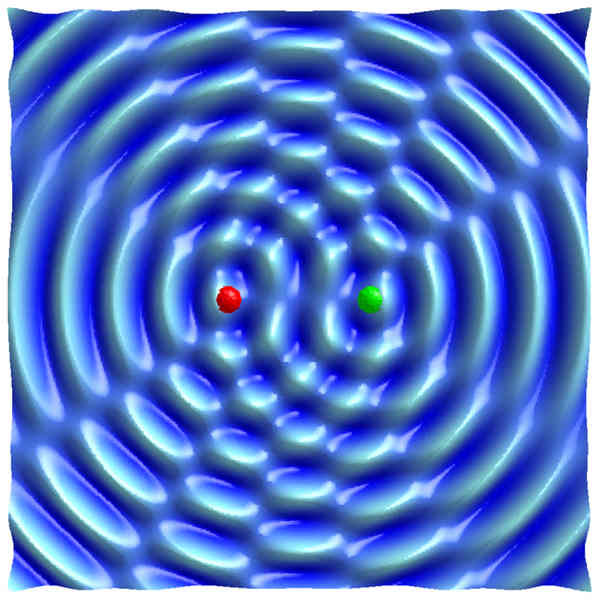
このように上から見ると、波の凹凸が奇妙なまでに消えている、曲線状の領域が数本走っている事が見て取れます。 わかりやすいように、上から線を描いてみたのが下図です(線は手でラフに引いたので、理論的に完璧に正確な線ではありません):
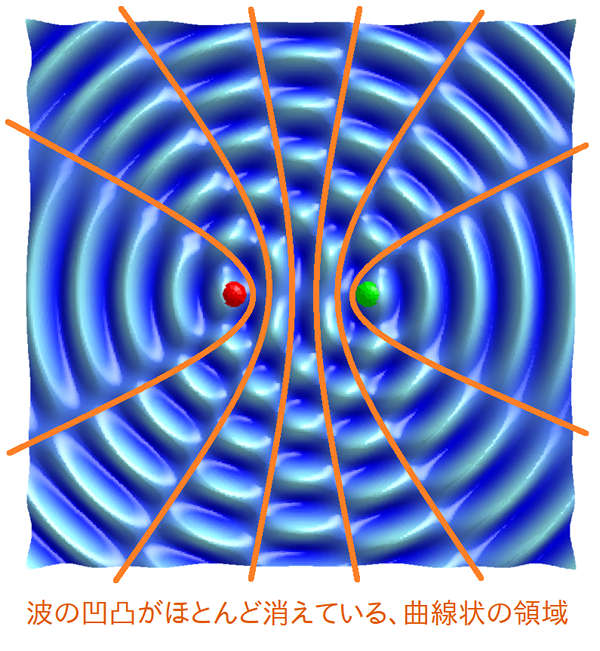
ここでアニメーションを見返すと、時間経過に伴って波が動いても、この線の上でだけ、常に凹凸が消えてしまう事が確認できます。 この線は一体何者なのでしょうか?
波Aと波Bが打ち消しあったり、強め合ったりする条件
実はこの線は、波Aと波Bが、常に互いにちょうど打ち消しあう、絶妙な条件を満たしている位置 に出現します。 具体的には、波源Aからの距離と、波源Bからの距離が、ちょうど波長の半分だけずれている位置に出現します。
それがどういう部分なのかを考えるために、もう一度、波Aだけの場合をふり返ってみましょう。 波源から少しずつ離れていくつもりで、波がどう変化していくのかを考えてみます。
いま扱っている円形波は、波源を含む断面が正弦波になるものでしたね。 正弦波は、山と谷が交互に来ます。 そして、正弦波のアニメーションの回で説明した通り、 1波長というのは、この山と谷を一個ずつ含む長さと一致するのでした。
という事は、波源からの距離が離れるのに伴って、ちょうど半波長(波長の半分)ごとに、山 → 谷 → 山 → 谷 … と交互に並んでいるはずです。 なお、波源の真上の位置が山なのか谷なのか、もしくは中途半端な状態なのかは、時間によって変化します。重要なのは、山と谷が半波長ごとに並ぶという事です。

上と全く同じ事が、波Bにも言えます。
さて、ここで再び、波Aと波Bの重ね合わせについて考えましょう。いまは、波源Aと波源Bは全く同じ振動をしています。 という事は、波源Aからの距離と、波源Bからの距離が、ちょうど同じ地点では、波Aで山がきている時に、波Bでも山がきます。 時間が少し経過して、同じ地点に今度は波Aで谷がきている時に、やはり波Bでも谷がきます。 他の中途半端な時間にも、結局は両者で全く同じように波が来るので、波Aと波Bを重ね合わせると、常に強め合います。
さらに、波源Aからの距離と、波源Bからの距離が、ちょうど波長の整数倍ずれている地点でも、同じように波Aと波Bは常に強め合います。 なぜなら、波源からの距離がちょうど1波長ずれると、そこからくる波がちょうど山と谷の一つぶんずれるので、山は山、谷は谷のままで、その地点の運動は変わらないからです。 なので、この地点では先に述べた、波源A・波源Bからの距離が等しい地点と全く同じ状況になり、波が強め合うのです。
そして本題です。波源Aからの距離と、波源Bからの距離が、ちょうど波長の整数倍 + 半波長(波長の半分)だけずれている地点では、波Aと波Bは打ち消しあいます。 なぜでしょうか?
先に述べた通り、2つの波源からの距離が波長の整数倍だけ違うの地点なら、波Aで山がきている時に、波Bでも山がきます。しかしそこから半波長だけずれると、状況はちょうど山1個分=谷1個分ずれる事になります。 そうすると、その地点で波Aで山がきている時に、波Bでは谷がきます。逆に波Aで谷がきている時には波Bでは山がきます。 じゃあ、山でも谷でもない中途半端な時間には? 実は、同じ正弦波を半波長の整数倍だけずらして合成すると、常に打ち消しあって波がゼロになります。 したがって結局、波源Aからの距離と、波源Bからの距離が、ちょうど半波長の整数倍だけずれている地点では、両者の波が時間によらず常に打ち消しあって、合成波の凹凸が消えてしまうのです。
波Aと波Bが打ち消しあう・強め合う線の形は?
先ほど見た、波の凹凸がほとんど消えている線は、「 波源Aからの距離と、波源Bからの距離がちょうど『波長の整数倍 + 半波長』だけ食い違っている 」という条件を満たす、都合のいい線になっています。 と言ってもそれほど特殊な線ではなく、中学校でも習う双曲線になっています。
実は双曲線は、「 ある二点からの距離の差が一定 」という面白い性質を持っています。 今回の場合は、「ある二点」が「波源Aと波源B」、「距離の差」というのが「波長の整数倍 + 半波長」になっていて、そういう双曲線上で、波Aと波Bが打ち消しあって凹凸が無くなっていたわけですね。
同様に、波源からの距離の差が、単純に波長の整数倍である領域も、双曲線を描きます。この条件を満たす地点では、先に述べた通り、波Aと波Bは常に強め合うのでしたね。 実はその線は、波が打ち消しあう双曲線の間に挟まれた領域を走っています。 改めてその領域を見ると、波の凹凸が消える事なく振動しています。 その、一番凹凸の激しい部分、つまり「こぶ」のピークが描く線が、波が強め合う条件を満たす双曲線となっています。
コード解説
このプログラムのコードはVCSSLで記述されています。 ここではそのコード内容について簡単に解説します。 VCSSLはC系の単純な文法の言語なので、C言語などに触れた事のある方なら簡単に読めると思います。
グラフの範囲などを変えたり、色々と改造したいといった場合などは、 プログラムのコード「 InterferingCircularWave.vcssl 」をテキストエディタで開いて改造してください。 スクリプト言語なので、コンパイラなどの別ソフトは不要で、コードを書き換えるだけでOKです。
前提となるコード
今回のコードは少し複雑なため、いきなり読むよりも、 より単純ないくつかのコードを踏まえた上での方が、読みやすくなると思います。
円形波をアニメーションさせる感覚や、パラメータ操作用にスライダーなどのGUI部品を組み立てる流れは、 前回のコードが参考になると思います:
ただし前回は、円形波をアニメーション表示する部分については、Graph3Dライブラリを用いて3Dグラフソフトに担わせていました。 その方がコードが単純で済みましたし、円形波を1個アニメーションさせるだけなら、グラフとして描いても十分わかりやすかったからです。
一方で今回は、波源として球を置いて動かしたり、波の面の色を細かく調整したりと、少し凝りたかったので、グラフソフトは使わずに描画処理のコードを書き下しています。 その部分が前回のコードと比べて増えています。
ただ、描画周りをゼロから用意するのはさすがに無駄に複雑になりすぎるので、 ある程度は土台の処理を代行してくれる簡易フレームワークである Graphics3DFramework ライブラリを使用しています。 このフレームワークを用いて、画面に曲面をアニメーション表示させる単純なサンプルとして、以下のコードがあります:
上のコードは60行程度の短いものですが、全体の構造や処理の流れが、ちょうど今回のプログラムのひな型とも言える形になっています。
今回のコードは、上の2つのプログラムのコードを合体させて、少し拡張したような具合になっています。 今回のコードを読む際に掴みどころが無いと感じた方は、事前に上記2つのコードを読んでみてください。
コード全体
それでは、今回のコードです。まずコードの全体を見てみましょう。
coding UTF-8; // 文字コードの明示(文字化け予防)
import Math; // 数学関数の使用に必要なライブラリの読み込み
import Graphics3D; // 3D描画関数を提供するライブラリの読み込み
import graphics3d.Graphics3DFramework; // 面倒な処理を代行してくれる3Dプログラム用レームワーク
// 以下、波のパラメータを格納する変数
double periodA = 1.0; // 波Aの周期(T)
double periodB = 1.0; // 波Bの周期
double wavelengthA = 1.0; // 波Aの波長(λ)
double wavelengthB = 1.0; // 波Bの波長
double amplitudeA = 0.12; // 波Aの振幅(A)
double amplitudeB = 0.12; // 波Bの振幅
double xA = -1.0; // 波源AのX座標
double xB = 1.0; // 波源BのX座標
double yA = 0.0; // 波源AのY座標
double yB = 0.0; // 波源BのY座標
// 範囲や点数、時間刻みなどの設定変数
const int N = 120; // メッシュの1方向あたり刻み数(大きいほど綺麗な反面、処理が重くなる)
const double X_MIN = -4.0; // グラフのX軸の最小値
const double X_MAX = 4.0; // グラフのX軸の最大値
const double Y_MIN = -4.0; // グラフのY軸の最小値
const double Y_MAX = 4.0; // グラフのY軸の最大値
const double Z_MIN = -2.0; // グラフのZ軸の最小値
const double Z_MAX = 2.0; // グラフのZ軸の最大値
const double DX = (X_MAX - X_MIN) / (N-1); // メッシュのX軸方向の刻み幅
const double DY = (Y_MAX - Y_MIN) / (N-1); // メッシュのY軸方向の刻み幅
const double DT = 0.1; // 1ループごとの時間進行量(speed=1.0の時の値)
// 波のデータ関連の変数
double waveVertex[ N ][ N ][ 3 ]; // 頂点座標値を格納する配列(最右次元は0=X,1=Y,2=Z)
const int X = 0; // 座標値配列で X 座標を表すインデックス
const int Y = 1; // 座標値配列で Y 座標を表すインデックス
const int Z = 2; // 座標値配列で Z 座標を表すインデックス
// 3DCG関連の変数
int waveModel; // モデルのIDを格納する
int waveCoordinate; // 波モデルを配置する座標系
int sourceCoordinateA; // 波源Aの球を配置する座標系
int sourceCoordinateB; // 波源Bの球を配置する座標系
// GUI関連の変数
int periodSliderA; // 波Aの周期設定スライダーのIDを格納する
int periodSliderB; // 波Bの周期設定スライダーのIDを格納する
int wavelengthSliderA; // 波Aの波長設定スライダーのIDを格納する
int wavelengthSliderB; // 波Bの波長設定スライダーのIDを格納する
int amplitudeSliderA; // 波Aの振幅設定スライダーのIDを格納する
int amplitudeSliderB; // 波Bの振幅設定スライダーのIDを格納する
int speedSlider; // アニメーション速度スライダーのIDを格納する
int infoLabelA; // 波Aの設定値を表示するラベルのIDを格納する
int infoLabelB; // 波Bの設定値を表示するラベルのIDを格納する
int timeLabel; // 時刻表示ラベルのIDを格納する
int resetButton; // 時刻リセットボタンのIDを格納する
// その他の制御関連の変数
double speed = 0.7; // アニメーション速度
double t = 0.0; // 時刻変数
// ==================================================
// この関数は、フレームワークから、
// プログラム起動後に1度だけコールされます。
// ==================================================
void onStart(int renderer){
// 波のパラメータの初期値を数値で入力するか尋ね、必要なら入力して設定
inputParameters();
// 画面サイズを設定
setWindowSize(820, 800);
// 色を鮮やかにするために環境光を明るめに設定
setAmbientLightBrightness(1.0);
// カメラ距離とカメラ倍率を設定
setGraphics3DMagnification(getRenderer(), 1400.0);
setGraphics3DDistance(getRenderer(), 20.0);
// 波座標系を生成
initializeCoordinate();
// 波モデルを生成して配置
initializeModel();
// 画面上のGUI部品を生成して配置
initializeGUI();
}
// ==================================================
// この関数は、フレームワークから、1秒間に数十回
//(フレームレート設定依存)繰り返しコールされます。
// ==================================================
void onUpdate(int renderer){
// 波モデルの頂点座標の更新
updateModelVertex();
// 波モデルの色の更新
updateModelColor();
// 波源の位置の更新
updateSourceLocations();
// 時刻を加算(アニメーション速度をかけて変化のスピードを調整)
t += DT * speed;
}
// ==================================================
// 起動時に波のパラメータの初期値を訪ねて入力する処理
// ==================================================
void inputParameters() {
if ( confirm("波のパラメータを数値で入力しますか?") ) {
amplitudeA = input("波Aの振幅=", amplitudeA);
amplitudeB = input("波Bの振幅=", amplitudeB);
wavelengthA = input("波Aの波長=", wavelengthA);
wavelengthB = input("波Bの波長=", wavelengthB);
periodA = input("波Aの周期=", periodA);
periodB = input("波Aの周期=", periodB);
}
}
// ==================================================
// 台座となる座標系を生成する処理
// ==================================================
void initializeCoordinate(){
// レンダラーのIDを取得(配置の際の引数に必要)
int renderer = getRenderer();
// 波モデルを配置する座標系(波座標系)を生成して配置
waveCoordinate = newCoordinate();
mountCoordinate(waveCoordinate, renderer);
// 波モデルの中心がワールド座標系の中心に来るよう移動
moveCoordinate(waveCoordinate, -(X_MAX+X_MIN)/2, -(Y_MAX+Y_MIN)/2, 0.0);
// 波源Aの座標系を生成し、波座標系上の波源の位置に配置
sourceCoordinateA = newCoordinate();
setCoordinateOrigin(sourceCoordinateA, xA, yA, 0.0);
mountCoordinate(sourceCoordinateA, renderer, waveCoordinate);
// 波源Bの座標系を生成し、波座標系上の波源の位置に配置
sourceCoordinateB = newCoordinate();
setCoordinateOrigin(sourceCoordinateB, xB, yB, 0.0);
mountCoordinate(sourceCoordinateB, renderer, waveCoordinate);
}
// ==================================================
// モデルを生成する処理
// ==================================================
void initializeModel(){
// レンダラーのIDを取得(配置の際の引数に必要)
int renderer = getRenderer();
// 四角形グリッド形式で波のモデル(波モデル)を生成して配置
waveModel = newModel(waveVertex, QUADRANGLE_GRID); // 生成
setModelColor(waveModel, 0, 0, 255, 255); // 色設定
setModelCull(waveModel, false, false); // 裏面カリング(描画省略)を無効化
mountModel(waveModel, renderer, waveCoordinate); // 配置
// 波源Aを表す球モデル(赤色)を、波源Aの座標系原点に配置
int sourceModelA = newSphereModel(0.2, 0.2, 0.2, 10, 8); // 生成
setModelColor(sourceModelA, 255, 0, 0, 255); // 色設定
mountModel(sourceModelA, renderer, sourceCoordinateA); // 配置
// 波源Bを表す球モデル(緑色)を、波源Bの座標系原点に配置
int sourceModelB = newSphereModel(0.2, 0.2, 0.2, 10, 8); // 生成
setModelColor(sourceModelB, 0, 255, 0, 255); // 色設定
mountModel(sourceModelB, renderer, sourceCoordinateB); // 配置
}
// ==================================================
// GUI部品の配置など、画面構築処理を行う処理
// ==================================================
void initializeGUI() {
// Graphics3DFramework で確保されているウィンドウのIDを取得(この上に部品を配置する)
int window = getWindow();
// ウィンドウ上部に余白を設定(GUI部品を配置するため)
setMarginTop(180);
// 時刻表示ラベルを生成して配置
timeLabel = newTextLabel( 10, 10, 200, 20, "" );
mountComponent( timeLabel, window );
// スライダーの左に振幅、周期、波長のラベルを生成して配置
int amplitudeLabel = newTextLabel( 45, 40, 100, 15, "A 振幅 (0〜1)" );
mountComponent( amplitudeLabel, window );
int omegaLabel = newTextLabel( 45, 60, 100, 15, "T 周期 (0.2〜5)" );
mountComponent( omegaLabel, window );
int lambdaLabel = newTextLabel( 45, 80, 100, 15, "λ 波長 (0.7〜4)" );
mountComponent( lambdaLabel, window );
// 振幅スライダー(範囲0.0〜1.0)を生成して配置
amplitudeSliderA = newHorizontalSlider( 150, 40, 300, 20, amplitudeA, 0.0, 1.0 );
amplitudeSliderB = newHorizontalSlider( 450, 40, 300, 20, amplitudeB, 0.0, 1.0 );
mountComponent( amplitudeSliderA, window );
mountComponent( amplitudeSliderB, window );
// 周期スライダー(範囲0.2〜5.0)を生成して配置
periodSliderA = newHorizontalSlider( 150, 60, 300, 20, periodA, 0.2, 5.0 );
periodSliderB = newHorizontalSlider( 450, 60, 300, 20, periodB, 0.2, 5.0 );
mountComponent( periodSliderA, window );
mountComponent( periodSliderB, window );
// 波長スライダー(範囲0.7〜4.0)を生成して配置
wavelengthSliderA = newHorizontalSlider( 150, 80, 300, 20, wavelengthA, 0.7, 4.0 );
wavelengthSliderB = newHorizontalSlider( 450, 80, 300, 20, wavelengthB, 0.7, 4.0 );
mountComponent( wavelengthSliderA, window );
mountComponent( wavelengthSliderB, window );
// スライダー値を表示するラベルを生成して配置
infoLabelA = newTextLabel( 155, 100, 300, 20, "" );
infoLabelB = newTextLabel( 455, 100, 300, 20, "" );
mountComponent( infoLabelA, window );
mountComponent( infoLabelB, window );
updateInfoLabel();
// 波Aと波Bの列を表すラベルを生成して配置
int columnLabelA = newTextLabel(280, 15, 200, 20, "波A(波源:赤)");
int columnLabelB = newTextLabel(580, 15, 200, 20, "波B(波源:緑)");
mountComponent( columnLabelA, window );
mountComponent( columnLabelB, window );
// アニメーション速度のラベルと調整スライダーを生成して配置
int speedLabel = newTextLabel( 10, 140, 140, 15, "アニメーション速度" );
mountComponent( speedLabel, window );
speedSlider = newHorizontalSlider( 150, 140, 400, 20, speed, 0.0, 1.0 );
mountComponent( speedSlider, window );
// 時刻リセットボタンを生成して配置
resetButton = newButton(600, 125, 150, 40, "時刻をリセット");
mountComponent( resetButton, window );
// 配置後にウィンドウを描画して表示内容を更新
paintComponent( window );
}
// ==================================================
// 波モデルの頂点座標を更新する処理
// ==================================================
void updateModelVertex() {
for( int yi=0; yi<N; yi++ ) {
for( int xi=0; xi<N; xi++ ) {
// 以下、メッシュモデル内の [yi][xi] 番目の頂点(格子点)に注目している
double x = X_MIN + xi * DX; // 注目頂点の x 座標値
double y = Y_MIN + yi * DY; // 注目頂点の y 座標値
double rA = sqrt( (x-xA)*(x-xA) + (y-yA)*(y-yA) ); // 波源Aからの距離
double rB = sqrt( (x-xB)*(x-xB) + (y-yB)*(y-yB) ); // 波源Bからの距離
// 円形波の式から、波源Aからの波(波A)と波源Bからの波(波B)のZ値をそれぞれに求める
double zA = amplitudeA * sin( 2.0 * PI * ( t/periodA - rA/wavelengthA ) ); // 波AのZ値
double zB = amplitudeB * sin( 2.0 * PI * ( t/periodB - rB/wavelengthB ) ); // 波BのZ値
// 頂点座標値配列に値を格納
waveVertex[yi][xi][X] = x;
waveVertex[yi][xi][Y] = y;
waveVertex[yi][xi][Z] = zA + zB; // 合成波のZ値は、重ね合わせの原理にり波Aと波Bの和
}
}
// モデルに頂点座標値配列を渡して形状を更新
setModelVertex(waveModel, waveVertex, QUADRANGLE_GRID);
}
// ==================================================
// 波モデルの色を更新する処理
// ==================================================
void updateModelColor() {
int polygonIndex = 0; // モデル内のポリゴンのインデックス
for( int yi=0; yi<N-1; yi++ ) { // メッシュの1方向あたりポリゴン数は頂点数-1なのでN-1
for( int xi=0; xi<N-1; xi++ ) {
// 以下、モデル内の polygonIndex 番目のポリゴンに注目している
// 波のZ値の最大値(振幅A+振幅B)が1、最小値が0となるようスケーリングしたZ比率を求める
double ratio = ( waveVertex[yi][xi][Z] / (amplitudeA + amplitudeB) + 1.0 ) / 2.0;
// 振幅Aと振幅Bが共に 0 の場合はZ比率が NaN や Inf になるので、その場合は 0 にする
if (nan(ratio) || inf(ratio)) {
ratio = 0.0;
}
// この処理中に振幅が変更されると、Z比率が 0〜1 の範囲を超える場合があるので、超過分を落とす
ratio = min(ratio, 1.0);
ratio = max(ratio, 0.0);
// Z比率の値を用いて、色のRGBA成分(それぞれ0〜255の範囲)を求める
int red = (int)(ratio * 160);
int green = (int)(ratio * 255);
int blue = 255;
int alpha = 255;
// ポリゴンの色を設定
setModelPolygonColor(waveModel, polygonIndex, red, green, blue, alpha);
// 次のループで次のポリゴンを処理する
polygonIndex++;
}
}
}
// ==================================================
// 波源の位置を更新する処理
// ==================================================
void updateSourceLocations() {
double sourceZA = amplitudeA * sin( 2.0 * PI * t/periodA ); // 波源AのZ値
double sourceZB = amplitudeB * sin( 2.0 * PI * t/periodB ); // 波源BのZ値
setCoordinateOrigin(sourceCoordinateA, xA, yA, sourceZA); // 波源Aの座標系の原点位置を設定
setCoordinateOrigin(sourceCoordinateB, xB, yB, sourceZB); // 波源Bの座標系の原点位置を設定
}
// ==================================================
// スライダー値を表示するラベルの内容を更新する処理
// ==================================================
void updateInfoLabel() {
string infoTextA
= "( A="
+ round(amplitudeA, 3, HALF_UP) // 振幅を小数点以下3桁に丸める
+ ", λ="
+ round(wavelengthA, 3, HALF_UP) // 波長を小数点以下3桁に丸める
+ ", T="
+ round(periodA, 3, HALF_UP) // 周期を小数点以下3桁に丸める
+ ")";
string infoTextB
= "( A="
+ round(amplitudeB, 3, HALF_UP) // 振幅を小数点以下3桁に丸める
+ ", λ="
+ round(wavelengthB, 3, HALF_UP) // 波長を小数点以下3桁に丸める
+ ", T="
+ round(periodB, 3, HALF_UP) // 周期を小数点以下3桁に丸める
+ ")";
setComponentString(infoLabelA, infoTextA);
setComponentString(infoLabelB, infoTextB);
paintComponent(infoLabelA);
paintComponent(infoLabelB);
paintComponent(getWindow());
}
// ==================================================
// スライダーが動いた際に呼ばれる処理(イベントハンドラ)
// ==================================================
void onSliderMove(int id, float value) {
// 以下、スライダーに対応するグローバル変数に値を設定
if(id == amplitudeSliderA) {
amplitudeA = value;
}
if(id == amplitudeSliderB) {
amplitudeB = value;
}
if(id == periodSliderA) {
periodA = value;
}
if(id == periodSliderB) {
periodB = value;
}
if(id == wavelengthSliderA) {
wavelengthA = value;
}
if(id == wavelengthSliderB) {
wavelengthB = value;
}
if (id == speedSlider) {
speed = value;
}
updateInfoLabel();
}
// ==================================================
// ボタンを押した際に呼ばれる処理(イベントハンドラ)
// ==================================================
void onButtonClick(int id) {
// 時刻リセットボタンが押されたら時刻変数 t をリセット
if (id == resetButton) {
t = 0.0;
}
}
以上です。大体400行ちょっとの規模のコードですね。 各部で行っている処理はコード内のコメントの通りですが、 以下では先頭から順を追って、もう少し詳しく説明します。
ただ、全部を詳しく追っていると量的に少し大変なので、 前提として挙げた 「 円形波のアニメーション表示 」のコード や 「 頂点配列によるモデルの変形アニメーション 」のコード とかぶっている部分は軽めに流し、 本質的に重要な部分をピックアップして見ていきます。
変数の宣言部
先頭から続く変数の宣言部では、基本的には前回のコードと同じで、 そこから波のパラメータや操作用スライダーなどの変数が、 波Aと波Bの2通りぶん用意されるようになっただけです。
ただし、波のデータを格納する頂点座標値配列が、以下のようにな形になっている点は、前回と異なります:
// 波のデータ関連の変数
double waveVertex[ N ][ N ][ 3 ]; // 頂点座標値を格納する配列(最右次元は0=X,1=Y,2=Z)
const int X = 0; // 座標値配列で X 座標を表すインデックス
const int Y = 1; // 座標値配列で Y 座標を表すインデックス
const int Z = 2; // 座標値配列で Z 座標を表すインデックス
前回は、X / Y / Z 座標についてそれぞれ別々に、waveX[N][N] / waveY[N][N] / waveZ[N][N] のような2次元配列を用意していましたね。 これは、そのほうが名前から X / Y / Z のどの座標なのかわかりやすかったのと、そのままグラフソフトに渡せる形で楽だったためです。
一方で今回は、グラフソフトではなくVCSSLの3DCG描画機能を用いて、波の形状のモデルを自分で作成して変形させます。 その際、モデルの頂点座標値を格納する配列は、上のコードのように、X / Y / Z 値も含めて1つにまとめ、[N][N][3] の形にしたほうが、 設定関数の引数で直接サポートされている下図の形に一致して、便利になります ( この形式について詳しくは 「 頂点配列によるモデルの変形アニメーション 」をご参照ください )。
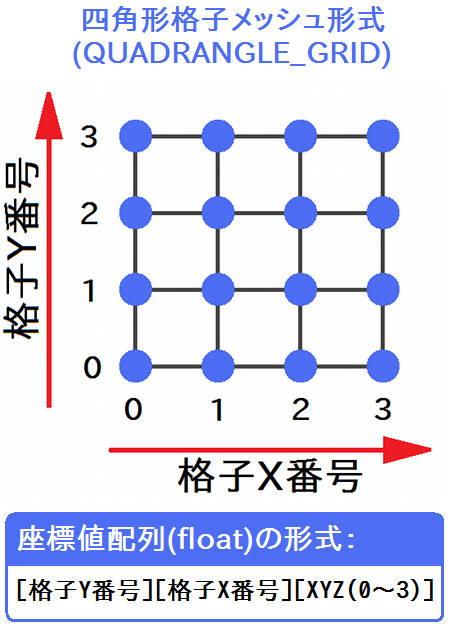
図の通り、この配列の一番右側の次元は、インデックス 0 でX値、インデックス 1 でY値、インデックス 2 でZ値を指します。 ただ、そのままだとコード内でわかりづらいため、 0 / 1 / 2 をそれぞれ int 型の定数 X / Y / Z で宣言しています。
これにより、たとえば上図のメッシュの縦に a、横に b 番目の点のX値を参照するのに、インデックスを [a][b][X] のように書けるようになります。
変数宣言部で前回から変化しているのは、こんなところです。本質的にはほとんど変わっていません。
プログラムの立ち上げ時の処理
続いて、プログラムを実行開始した後に実行される、初期化などの立ち上げ時の処理を見てみましょう。
少し前に述べた通り、このプログラムは3Dプログラム用の簡易フレームワーク Graphics3DFramework を使用しています。 ウィンドウやレンダラー(描画エンジン)の生成などの、大抵の3Dプログラムで共通になるような土台の処理は、起動後にまずフレームワークが自動にやってくれます。 それが済むと、フレームワークは onStart 関数が宣言されていれば呼び出してくれる仕組みになっています。
従って、onStart 関数を宣言して、そこにプログラム起動後に一度だけ行いたい処理を記述します。 今回は以下のように記述しています:
// ==================================================
// この関数は、フレームワークから、
// プログラム起動後に1度だけコールされます。
// ==================================================
void onStart(int renderer){
// 波のパラメータの初期値を数値で入力するか尋ね、必要なら入力して設定
inputParameters();
// 画面サイズを設定
setWindowSize(820, 800);
// 色を鮮やかにするために環境光を明るめに設定
setAmbientLightBrightness(1.0);
// カメラ距離とカメラ倍率を設定
setGraphics3DMagnification(getRenderer(), 1400.0);
setGraphics3DDistance(getRenderer(), 20.0);
// 波座標系を生成
initializeCoordinate();
// 波モデルを生成して配置
initializeModel();
// 画面上のGUI部品を生成して配置
initializeGUI();
}
まずは、ユーザーが波のパラメータを数値入力したい場合のために、inputParameters 関数を呼び出して、必要に応じてパラメータ入力処理を行っています。 この関数は同じコード内に宣言されていますが、前回と基本的に同じで、波が2個に増えているだけなので、割愛しましょう。
続いて、setWindowSize 関数で画面サイズを、 setAmbientLightBrightness 関数で環境光の明るさを設定していますが、 これらはフレームワーク側で用意されている設定関数です。 また、その後でカメラ周りの設定を行っている setGraphics3DMagnification 関数や setGraphics3DDistance 関数は、3DCGの各種描画機能を提供する Graphics3D ライブラリの関数です。
このあたりでは、引数に数字をベタ書きしていてお行儀が悪いですが、単発のシミュレーションコードのためご容赦ください。
ここからはちょっと重要な部分です。まず initializeCoordinate 関数で座標系を生成して組み立て、initializeModel 関数でその上にモデルを生成して配置しています。 これらの関数はコード内で宣言されていて、その中身は:
// ==================================================
// 台座となる座標系を生成する処理
// ==================================================
void initializeCoordinate(){
// レンダラーのIDを取得(配置の際の引数に必要)
int renderer = getRenderer();
// 波モデルを配置する座標系(波座標系)を生成して配置
waveCoordinate = newCoordinate();
mountCoordinate(waveCoordinate, renderer);
// 波モデルの中心がワールド座標系の中心に来るよう移動
moveCoordinate(waveCoordinate, -(X_MAX+X_MIN)/2, -(Y_MAX+Y_MIN)/2, 0.0);
// 波源Aの座標系を生成し、波座標系上の波源の位置に配置
sourceCoordinateA = newCoordinate();
setCoordinateOrigin(sourceCoordinateA, xA, yA, 0.0);
mountCoordinate(sourceCoordinateA, renderer, waveCoordinate);
// 波源Bの座標系を生成し、波座標系上の波源の位置に配置
sourceCoordinateB = newCoordinate();
setCoordinateOrigin(sourceCoordinateB, xB, yB, 0.0);
mountCoordinate(sourceCoordinateB, renderer, waveCoordinate);
}
// ==================================================
// モデルを生成する処理
// ==================================================
void initializeModel(){
// レンダラーのIDを取得(配置の際の引数に必要)
int renderer = getRenderer();
// 四角形グリッド形式で波のモデル(波モデル)を生成して配置
waveModel = newModel(waveVertex, QUADRANGLE_GRID); // 生成
setModelColor(waveModel, 0, 0, 255, 255); // 色設定
setModelCull(waveModel, false, false); // 裏面カリング(描画省略)を無効化
mountModel(waveModel, renderer, waveCoordinate); // 配置
// 波源Aを表す球モデル(赤色)を、波源Aの座標系原点に配置
int sourceModelA = newSphereModel(0.2, 0.2, 0.2, 10, 8); // 生成
setModelColor(sourceModelA, 255, 0, 0, 255); // 色設定
mountModel(sourceModelA, renderer, sourceCoordinateA); // 配置
// 波源Bを表す球モデル(緑色)を、波源Bの座標系原点に配置
int sourceModelB = newSphereModel(0.2, 0.2, 0.2, 10, 8); // 生成
setModelColor(sourceModelB, 0, 255, 0, 255); // 色設定
mountModel(sourceModelB, renderer, sourceCoordinateB); // 配置
}
のようになっています。
座標系は基本的に、モデルの配置位置や角度を調整したり、動かしたりするのに使用します( VCSSL 3DCG開発ガイド「 座標系の考え方と生成・配置 」参照)。
今回の初期設定だと、波モデルは普通に3D空間に(ワールド座標系上に)直接配置しても別に問題ないのですが、 そのままだと、波の中で画面に表示する範囲を決める X_MAX や Y_MIN などの設定値次第では、画面のすごい端のほう(または遥か彼方)に波が表示されてしまいます。 なので、常に波の表示部分(波モデル)の中心が3D空間の中心(ワールド座標系の原点)に一致するように適時オフセットして配置したいので、 土台となる座標系(以下、波座標系)を一つ配置して、その上に波モデルを配置するようにしています。
波モデルを生成している newModel 関数の引数に QUADRANGLE_GRID を指定していますが、 これは先に述べた格子状の形式の頂点座標値配列から、曲面形状のモデルを生成するためのオプションです ( 詳しくは 「 頂点配列によるモデルの変形アニメーション 」をご参照ください )。
波源A,Bについては、時間と共に常に動くため、やはりそれぞれに土台となる座標系(以下、波源座標系)を生成して波座標系上に配置し、その上に波源のモデルを配置しています。 波源を動かす際は、この波源座標系の原点位置を動かします。そうすると、その上に配置されている波源のモデルも一緒に動きます。
立ち上げ時の処理で残っているのは、GUI部品の配置などの画面構築処理を行う initializeGUI 関数(同じコード内で宣言)ですが、 これは前回とほぼ同じで、スライダーの個数が増えているくらいなので、割愛して先に進みます。
アニメーション処理
続いて、波をアニメーションさせる処理です。
前回のコードでは、main 関数内にアニメーションループを設けて、パラパラ漫画の要領で小刻みに時間を進めながら、 少しずつ違う波のデータをグラフソフトに渡して描画させていました。それを高速にくりかえす事で、アニメーションで動くように見えたわけですね。
その基本的な考え方自体は、今回も同じです。ただ今回は、アニメーションループはフレームワーク側が回してくれています。 そして、アニメーションループを一周するごとに、onUpdate 関数を呼び出してくれます。
つまり、コード内で onUpdate 関数を宣言さえしておけば、あとはそれが自動で毎秒数十回ほど呼び出されるので、 その中で波の形(や色)を毎回少しずつ変化させるようにすれば、アニメーションして見えます。楽ですね。
実際の onUpdate 関数の記述内容は以下の通りです:
// ==================================================
// この関数は、フレームワークから、1秒間に数十回
//(フレームレート設定依存)繰り返しコールされます。
// ==================================================
void onUpdate(int renderer){
// 波モデルの頂点座標の更新
updateModelVertex();
// 波モデルの色の更新
updateModelColor();
// 波源の位置の更新
updateSourceLocations();
// 時刻を加算(アニメーション速度をかけて変化のスピードを調整)
t += DT * speed;
}
まずは updateModelVertex 関数を呼び出し、頂点座標値配列を更新してモデルの形を変化させています。 この関数は同じコード内で以下のように宣言されていています:
// ==================================================
// 波モデルの頂点座標を更新する処理
// ==================================================
void updateModelVertex() {
for( int yi=0; yi<N; yi++ ) {
for( int xi=0; xi<N; xi++ ) {
// 以下、メッシュモデル内の [yi][xi] 番目の頂点(格子点)に注目している
double x = X_MIN + xi * DX; // 注目頂点の x 座標値
double y = Y_MIN + yi * DY; // 注目頂点の y 座標値
double rA = sqrt( (x-xA)*(x-xA) + (y-yA)*(y-yA) ); // 波源Aからの距離
double rB = sqrt( (x-xB)*(x-xB) + (y-yB)*(y-yB) ); // 波源Bからの距離
// 円形波の式から、波源Aからの波(波A)と波源Bからの波(波B)のZ値をそれぞれに求める
double zA = amplitudeA * sin( 2.0 * PI * ( t/periodA - rA/wavelengthA ) ); // 波AのZ値
double zB = amplitudeB * sin( 2.0 * PI * ( t/periodB - rB/wavelengthB ) ); // 波BのZ値
// 頂点座標値配列に値を格納
waveVertex[yi][xi][X] = x;
waveVertex[yi][xi][Y] = y;
waveVertex[yi][xi][Z] = zA + zB; // 合成波のZ値は、重ね合わせの原理にり波Aと波Bの和
}
}
// モデルに頂点座標値配列を渡して形状を更新
setModelVertex(waveModel, waveVertex, QUADRANGLE_GRID);
}
ここでは、メッシュ内の格子点を走査しながら、各地点の波源Aと波源Bからの距離を、それぞれ rA と rB に求めています。 ここで波源の位置 \( ( x_A, y_A ) \) から注目点 \( ( x, y ) \) までの間の距離 \( r_A \) は、
\[ r_A = \sqrt{ (x-x_A)^2 + (y-y_A)^2 } \tag{1} \]で表されるので、それをそのままプログラムの形にしています(ルートは sqrt 関数になります)。 そしてその値に基づき、前回扱った円形波の式:
\[ z = A \sin 2 \pi \bigg( \frac{t}{T} - \frac{r}{\lambda} \bigg) \tag{2} \]から、波Aと波Bの値をそれぞれ zA と zB に求めています。そして、それらを重ね合わせて(単純に和をとって)、頂点座標値配列の z 値として格納しています。 あとは、頂点座標値配列を Graphics3D ライブラリの setModelVertex 関数に渡して、波モデルの形状を更新しています。 これでこの updateModelVertex 関数の処理は終わりです。
さて、その後は、波モデルの色を更新する updateModelColor 関数を実行しています。 これもコード内で宣言している関数で、以下のような内容になっています:
// ==================================================
// 波モデルの色を更新する処理
// ==================================================
void updateModelColor() {
int polygonIndex = 0; // モデル内のポリゴンのインデックス
for( int yi=0; yi<N-1; yi++ ) { // メッシュの1方向あたりポリゴン数は頂点数-1なのでN-1
for( int xi=0; xi<N-1; xi++ ) {
// 以下、モデル内の polygonIndex 番目のポリゴンに注目している
// 波のZ値の最大値(振幅A+振幅B)が1、最小値が0となるようスケーリングしたZ比率を求める
double ratio = ( waveVertex[yi][xi][Z] / (amplitudeA + amplitudeB) + 1.0 ) / 2.0;
// 振幅Aと振幅Bが共に 0 の場合はZ比率が NaN や Inf になるので、その場合は 0 にする
if (nan(ratio) || inf(ratio)) {
ratio = 0.0;
}
// この処理中に振幅が変更されると、Z比率が 0〜1 の範囲を超える場合があるので、超過分を落とす
ratio = min(ratio, 1.0);
ratio = max(ratio, 0.0);
// Z比率の値を用いて、色のRGBA成分(それぞれ0〜255の範囲)を求める
int red = (int)(ratio * 160);
int green = (int)(ratio * 255);
int blue = 255;
int alpha = 255;
// ポリゴンの色を設定
setModelPolygonColor(waveModel, polygonIndex, red, green, blue, alpha);
// 次のループで次のポリゴンを処理する
polygonIndex++;
}
}
}
何をやっているかというと、 波を真上から見た際に振動の激しい所とそうでない所を見分けやすいように、 波モデルをZ値に基づくグラデーションで彩色しています。 各行の処理はコメントの通りです。波のカラーリングを変えたい場合は、このあたりを改造してください。 ただ、派手な色にすると、動きとあいまって非常に気持ち悪い雰囲気になるので、ご注意ください(昔、赤→緑→青へのグラデーションにした事があるのですが、絶不評でした)。
これで波モデルのアニメーション処理は終わりですが、忘れてはいけないのが、波源のアニメーションです。 上の関数の後に updateSourceLocations 関数が呼ばれ、そこで波源の位置が更新されます。これもコード内で宣言されていて、内容は以下の通りです:
// ==================================================
// 波源の位置を更新する処理
// ==================================================
void updateSourceLocations() {
double sourceZA = amplitudeA * sin( 2.0 * PI * t/periodA ); // 波源AのZ値
double sourceZB = amplitudeB * sin( 2.0 * PI * t/periodB ); // 波源BのZ値
setCoordinateOrigin(sourceCoordinateA, xA, yA, sourceZA); // 波源Aの座標系の原点位置を設定
setCoordinateOrigin(sourceCoordinateB, xB, yB, sourceZB); // 波源Bの座標系の原点位置を設定
}
波源Aと波源Bについては、当然ながら波源からの距離 \( r \) はゼロなので、円形波の (2) 式で \( -r/\lambda \) の部分は消えます。 その式でそのまま波源のZ座標を求めて、波源座標系の原点位置をその位置になるよう更新しています。 波源モデルである赤色と緑色のボールは、波源座標系の上に配置されているので、波源座標系の原点位置を動かせば、一緒に動きます。
その他の部分
主要な部分については、これで全部です。その他の部分は、大体 前回のコード や 前々回のコード と同様で、それも細かい枝葉の処理やイベントハンドラなどです。
コード内容は以上です。
ライセンス
このVCSSL/Vnanoコード( 拡張子が「.vcssl」や「.vnano」のファイル )は実質的な著作権フリー(パブリックドメイン) である CC0 の状態で公開しています※。 記事中にC言語/C++/Java言語などでのサンプルコードが掲載されいてる場合は、それらについても同様です。 そのままでのご利用はもちろん、改造や流用などもご自由に行ってください。
※ ただし、このコードの配布フォルダ内には、ダウンロード後すぐに実行できるように、 VCSSLの実行環境も同梱されており、そのライセンス文書は「 License 」フォルダ内に同梱されています (要約すると、商用・非商用問わず自由に使用できますが、使用の結果に対して開発元は一切の責任を負いません、といった具合の内容です)。 配布フォルダ内の各構成物の一覧やライセンスについては「 ReadMe_使用方法_必ずお読みください.txt 」をご参照ください。
※ Vnano の実行環境については、別途スクリプトエンジンのソースコードも一般公開しており、 何らかのソフトウェア内に組み込んでご利用いただく事も可能です。詳細はこちらをご参照ください。
この記事中の商標などについて
- OracleとJavaは、Oracle Corporation 及びその子会社、関連会社の米国及びその他の国における登録商標です。文中の社名、商品名等は各社の商標または登録商標である場合があります。
- Windows は、米国 Microsoft Corporation の米国およびその他の国における登録商標です。この記事は独立著作物であり、Microsoft Corporation と関連のある、もしくはスポンサーを受けるものではありません。
- Linux は、Linus Torvalds 氏の米国およびその他の国における商標または登録商標です。
- その他、文中に使用されている商標は、その商標を保持する各社の各国における商標または登録商標です。
|
Vnano版 | ローレンツ方程式を数値的に解くプログラム |
|
|
|
ローレンツ方程式を4次ルンゲ=クッタ法によって解き、グラフ描画用のデータを出力するプログラムです。 |
|
波の干渉(面上の円形波)のアニメーション表示 |
|
|
|
面上の円形波が干渉する様子を、パラメータを操作しながらアニメーションで見られるプログラムです。 |
|
円形波のアニメーション表示 |
|
|
|
振幅・波長・周期をスライダ―で操作しながら、円形波のグラフをアニメーションで見られるプログラムです。 |
|
波の干渉(線上の正弦波)のアニメーション表示 |
|
|
|
線上(1次元の)の正弦波が干渉する様子を、パラメータを操作しながらアニメーションで見られるプログラムです。 |
|
正弦波のアニメーション表示 |
|
|
|
振幅・波長・周期をスライダ―で操作しながら、正弦波のグラフをアニメーションで見られるプログラムです。 |
|
凹レンズを通過する波のシミュレーション |
|
|
|
凹レンズ形状の高密度媒質を通過する、波のシミュレーションです。 |
|
凸レンズを通過する波のシミュレーション |
|
|
|
凸レンズ形状の高密度媒質を通過する、波のシミュレーションです。 |
|
乱雑な密度分布における波のシミュレーション |
|
|
|
密度分布が乱雑な媒質中における、波の伝播のシミュレーションです。 |
|
ローレンツアトラクタ(ファイル出力版) |
|
|
|
4次精度ルンゲ=クッタ法により、ローレンツアトラクタを求めるプログラムです。 |
|
波の屈折のシミュレーション |
|
|
|
密度の異なる領域を、波が屈折しながら通過するシミュレーションです。 |
|
力学アルゴリズムによる波のシミュレーション(面上の波) |
|
|
|
媒質をバネと格子点で近似し、力学的なアルゴリズムで動かす事による、波のシミュレーションです。 |
|
手動で波を発生させるシミュレーション |
|
|
|
スライダーをマウスで動かす事により、波を発生させるシミュレーションです。 |
|
力学アルゴリズムによる波のシミュレーション(線上の波) |
|
|
|
媒質をバネと格子点で近似し、力学的なアルゴリズムで動かす事による、波のシミュレーションです。 |
|
二重振り子のシミュレーション |
|
|
|
ラグランジュ方程式を用いた、二重振り子のシミュレーションです。 |
|
ローレンツアトラクタ(GUI版) |
|
|
|
4次精度ルンゲ=クッタ法により、ローレンツアトラクタを求めるプログラムです。 |