» 詳しい使用方法や、エラーで展開できない際の対応方法などはこちら
波の干渉(線上の正弦波)のアニメーション表示
線上の(1次元の)正弦波が干渉する様子を再現する、VCSSL製の簡易シミュレーターです。
前回は単純な正弦波のアニメーションを扱いましたが、今回はその続きです。 そもそも正弦波とは? という場合は、まずは前回の内容をご参照ください。 今回は前回の続きとして、正弦波を2つ重ね合わせて、干渉する様子をアニメーション表示してみましょう。
[ 関連記事 ]
- 前回: 正弦波のアニメーション表示
使用方法
ダウンロードと展開(解凍)
まず、PC(スマホは未対応)で上の画面の「 ダウンロード 」ボタンを押してください。 するとZIP形式で圧縮されたファイルがダウンロードされます。
その後、ZIPファイルを右クリックして「すべて展開」や「ここに展開」などで展開(解凍)してください。 展開が成功すると、ZIPファイルと同じ名前のフォルダができ、その中にZIPファイルの中身が入っています。
» 展開がエラーで止まってしまう場合や、ファイル名が文字化けしてしまう場合は…
プログラムの起動
Windows をご使用の場合
上記でZIPファイルを展開したフォルダ内にある、以下のバッチファイルをダブルクリック実行してください:
もしプログラムを書き変えながら使いたい場合は、代わりに「 VCSSL_Editor__プログラム編集はこちら.bat 」を実行してください。
正常に起動できると、初回のみ、Java実行環境を入手するか等を尋ねられるので、適時答えて済ませると、プログラムが起動します。 2回目以降はすぐに起動します。
Linux 等をご使用の場合
ZIPファイルを展開したフォルダ内へコマンドライン端末で cd して、以下の通り入力して実行してください:
(プログラムの内容を書き変えながら使いたい場合は、代わりに VCSSL_Editor.jar を実行)
» javaコマンドが使用できない等のエラーが表示される場合は…
起動後の画面
起動すると、まず波のパラメータを数値入力するか尋ねられます。 特に「ぴったりこの値の波長にしたい」などの必要が無ければ、「いいえ」でスキップして構いません。
その後、グラフ画面とパラメータ設定画面が立ち上がります。
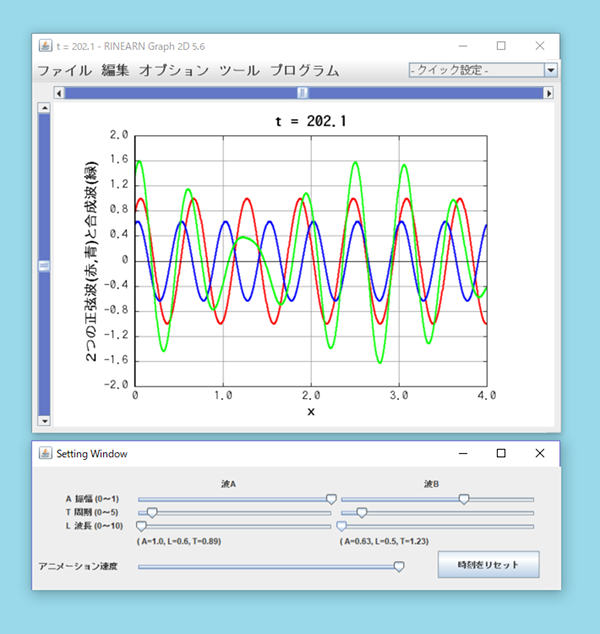
グラフ画面では、正弦波がアニメーション表示されます。 赤色と青色の線が、重ね合わせる2つの波(波Aと波B)です。緑色※ の線は、重ねあわされた結果の合成波です。 パラメータ設定画面では、波長や振幅、周期などの値を、波Aと波Bでそれぞれ独立にスライダーで操作できます。
ウィンドウを閉じると、プログラムの実行が終了します。
赤色と緑色が見分けづらく、波Aと合成波がまぎらわしい場合は、グラフ画面上部のメニューバーから、[ 編集 」> 「 色の設定 」メニューを選択すると、 それぞれの波の色を自由に変更する事ができます。
色の設定画面において、系列の No.1 が波A、No.2 が波B、No.3 が合成波です。たとえば、No.3 を「 BLACK 」に設定すると、合成波が、緑色の代わりに黒色で表示されるようになります。
題材解説
複数の異なる波を重ね合わせると、元のどちらの波とも違った形(と動き)をする波ができます。これを干渉といいます。
例えば、正弦波は sin 関数の形をしていますが、波長のみが微妙に異なる正弦波を重ね合わせて干渉させると、 x 軸上で振幅が大きい所と小さい所(ほぼゼロの点も)が交互に出現する、歪んだ正弦波のような独特のパターンが表れます(下図の緑色の線)。
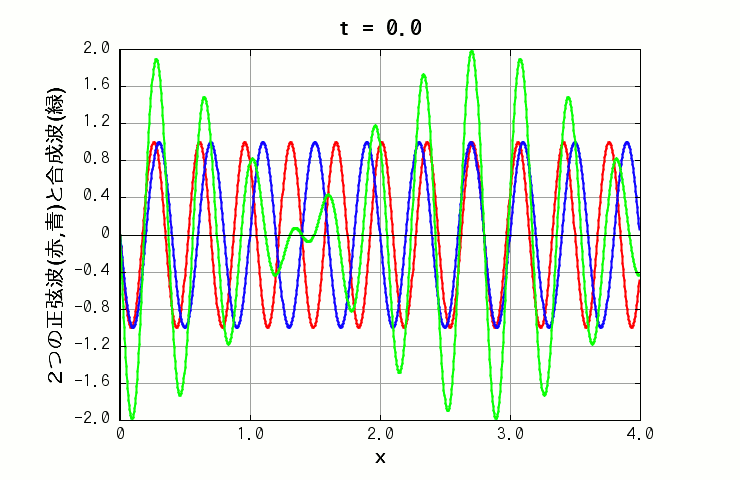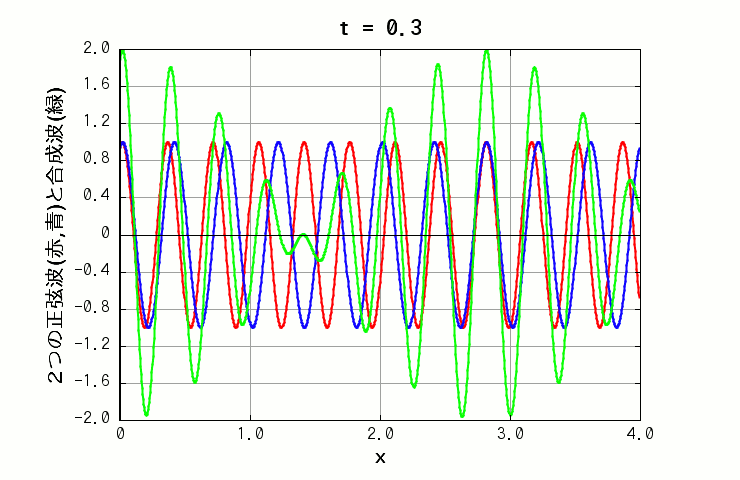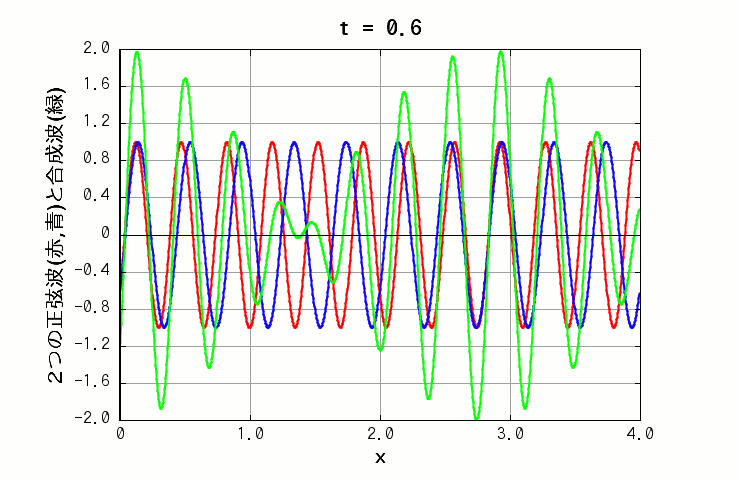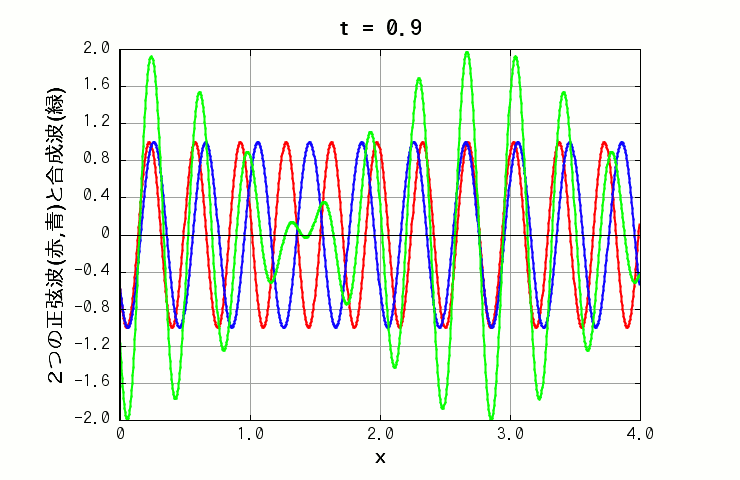
( 波A: 振幅=1.0, 波長=0.35, 周期=1.0 波B: 振幅=1.0, 波長=0.4, 周期=1.0 )
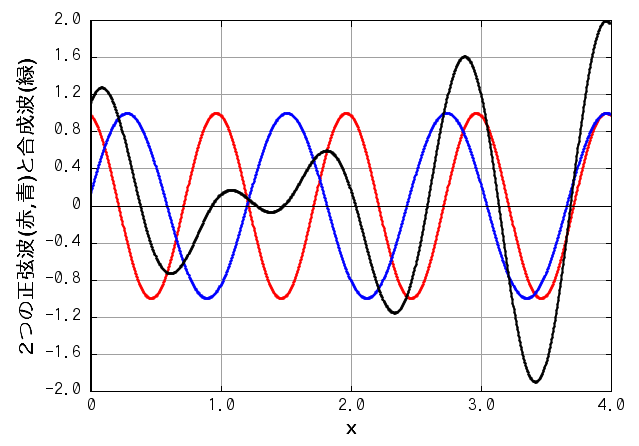
また、周期のみが異なる場合は、同じ x の位置でも、振幅が時間によって大きくなったり小さくなったりします(下図の緑色の線)。いわゆる「うなり」です。
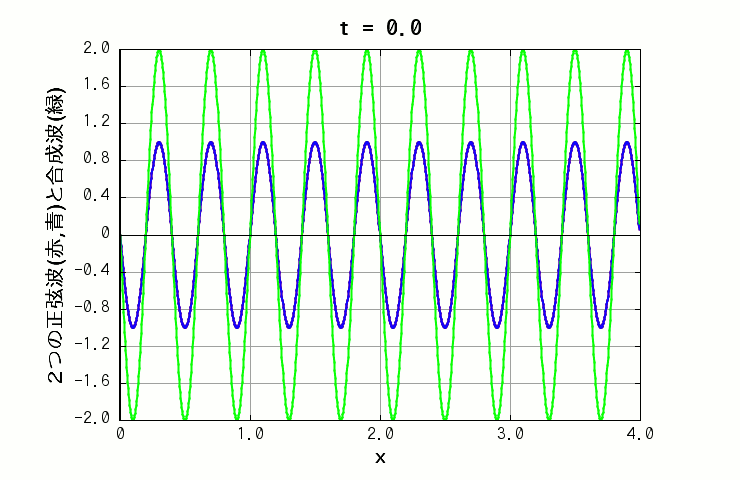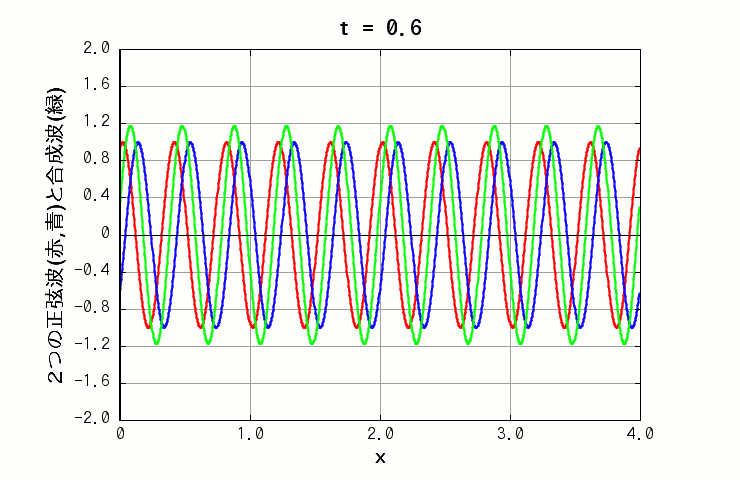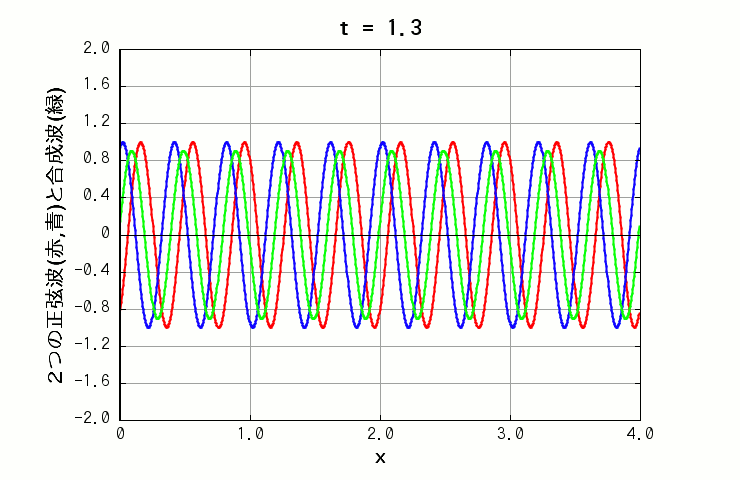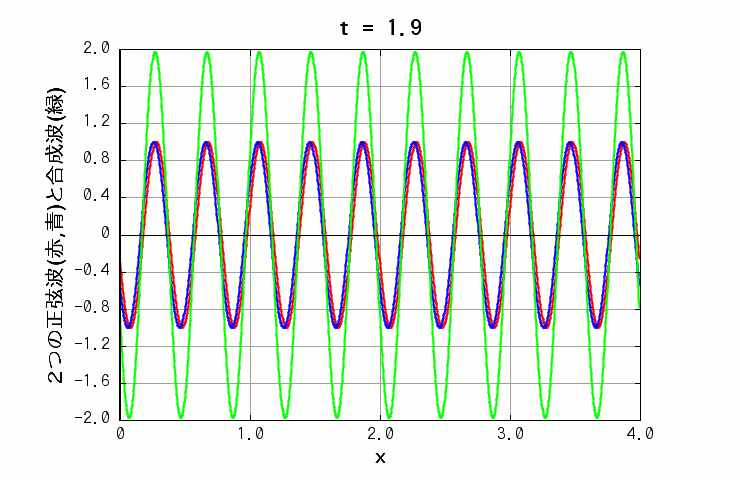
( 波A: 振幅=1.0, 波長=0.4, 周期=2.0 波B: 振幅=1.0, 波長=0.4, 周期=1.0 )
波長も振動数も違う波を重ね合わせた場合は、x 軸上の独特のパターンが、時間経過によって移動していく様子を見る事ができます(下図の緑色の線)。
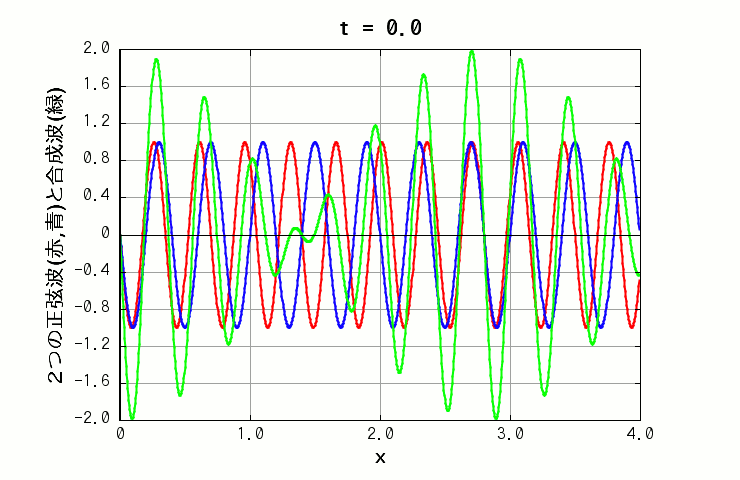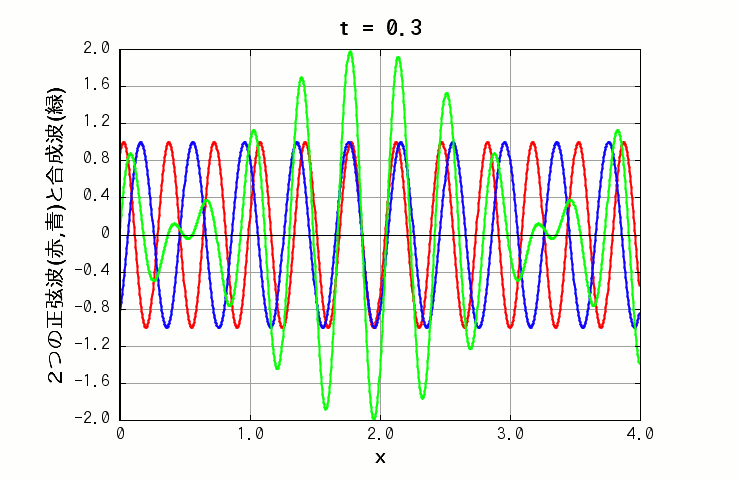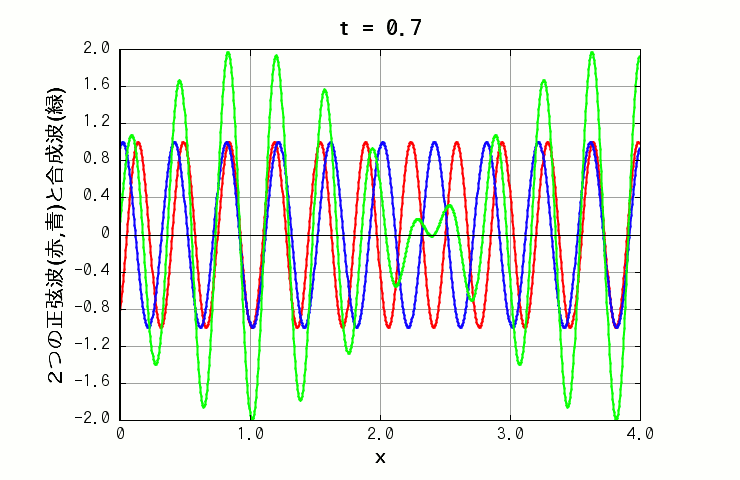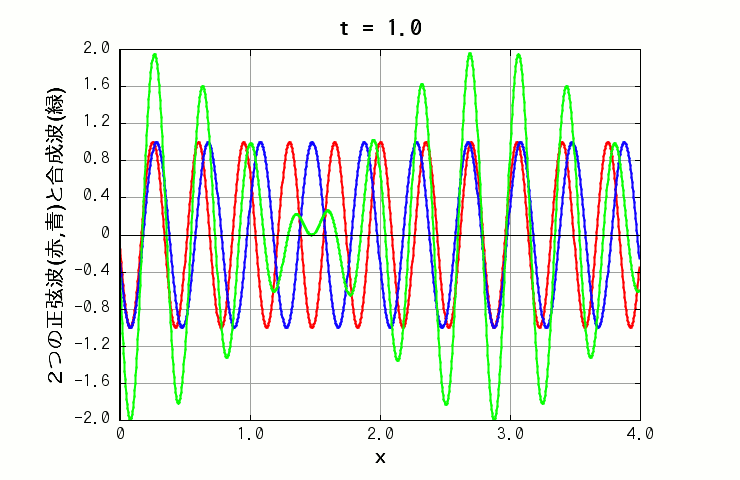
( 波A: 振幅=1.0, 波長=0.35, 周期=1.0 波B: 振幅=1.0, 波長=0.4, 周期=0.5 )
面白いのは、振幅の大小のパターンが移動していく向きや速さと、その中にある(歪んだ)正弦波の波が移動していく向きや速さが、一般には全然違うという点です。 前者の速度は群速度、後者の速度は位相速度と呼ばれます。
位相速度は、単体の正弦波にもあって、その場合は要するに波の速さそのものです。近い波長と周期の波を重ね合わせた合成波の位相速度は、ほぼ元の波の位相速度のままです。
一方で群速度は、重ね合わせる2つの正弦波の、「波長の差」と「周期の差」(または波数の差と角振動数の差)の比率によって決まります。 なお、波長や周期が連続的に違う波を無数に重ね合わせる場合は、差の比率の代わりに微分になります。
コード解説
このプログラムのコードはVCSSLで記述されています。 ここではそのコード内容について簡単に解説します。 VCSSLはC系の単純な文法の言語なので、C言語などに触れた事のある方なら簡単に読めると思います。
グラフの範囲などを変えたり、色々と改造したいといった場合などは、 プログラムのコード「 SineWave.vcssl 」をテキストエディタで開いて改造してください。 スクリプト言語なので、コンパイラなどの別ソフトは不要で、コードを書き換えるだけでOKです。
コード全体
まずは、コード全体を見てみましょう。
coding UTF-8; // 文字コードの明示(文字化け予防)
import Math; // 数学関数の使用に必要なライブラリの読み込み
import GUI; // GUI画面の構築に必要なライブラリの読み込み
import tool.Graph2D; // 2次元グラフ描画に必要なライブラリの読み込み
// 以下、波のパラメータを格納する変数
double amplitudeA = 1.0; // 波Aの振幅(A)
double amplitudeB = 1.0; // 波Bの振幅(A)
double wavelengthA = 0.35; // 波Aの波長(λ)
double wavelengthB = 0.4; // 波Bの波長(λ)
double periodA = 1.0; // 波Aの周期(T)
double periodB = 0.5; // 波Bの周期(T)
// グラフ範囲や点数、時間刻みなどの設定変数
const int N = 1024; // グラフの点数(細かいほど滑らか)
const double X_MIN = 0.0; // グラフのX軸の最小値
const double X_MAX = 4.0; // グラフのX軸の最大値
const double Y_MIN = -2.0; // グラフのY軸の最小値
const double Y_MAX = 2.0; // グラフのY軸の最大値
const double DT = 0.05; // 1ループごとの時間進行量(speed=1.0の時の値)
const double DX = (X_MAX - X_MIN) / N; // 1頂点ごとのX軸進行量
// グラフに波のデータを渡すための座標値配列
double waveX[ 3 ][ N ]; // X座標の配列 / 波A,波B,合成波の合計3系列 × 座標点数
double waveY[ 3 ][ N ]; // Y座標の配列 / 波A,波B,合成波の合計3系列 × 座標点数
// GUI(設定画面)用の変数
int window; // ウィンドウのIDを格納する
int periodSliderA; // 波Aの周期設定スライダーのIDを格納する
int periodSliderB; // 波Bの周期設定スライダーのIDを格納する
int wavelengthSliderA; // 波Aの波長設定スライダーのIDを格納する
int wavelengthSliderB; // 波Bの波長設定スライダーのIDを格納する
int amplitudeSliderA; // 波Aの振幅設定スライダーのIDを格納する
int amplitudeSliderB; // 波Bの振幅設定スライダーのIDを格納する
int speedSlider; // アニメーション速度スライダーのIDを格納する
int infoLabelA; // 波Aの設定値を表示するラベルのIDを格納する
int infoLabelB; // 波Bの設定値を表示するラベルのIDを格納する
int timeLabel; // 時刻表示ラベルのIDを格納する
int resetButton; // 時刻リセットボタンのIDを格納する
// その他の制御用変数
float speed = 0.5; // アニメーション速度
int graph; // グラフソフトのIDを格納する
bool continuesLoop = true; // アニメーションON/OFF制御変数
double t; // 時刻変数
// ==================================================
// 中心的な処理 - この関数は起動時に自動で実行されます
// ==================================================
void main( ){
// 波のパラメータの初期値を数値で入力するか尋ね、必要なら入力して設定
inputParameters();
// グラフを起動
createGraphWindow();
// GUI(設定画面)を構築
createSettingWindow();
t = 0.0; // 時刻を0に設定
// アニメーションのループ
while( continuesLoop ) {
// グラフのタイトルに時刻を表示する
string roundedTime = round(t, 1, HALF_UP); // 時刻を小数点以下1桁に丸める
setGraph2DTitle(graph, "t = " + roundedTime); // タイトルを「 t = 時刻 」に設定
// グラフソフトに渡す点列データの座標を計算
for( int i=0; i<N; i++ ) {
double x = X_MIN + i * DX; // i番目の点のx座標値
// 波A
waveX[ 0 ][ i ] = x;
waveY[ 0 ][ i ] = amplitudeA * sin( 2.0 * PI * ( t/periodA - x/wavelengthA ) );
// 波B
waveX[ 1 ][ i ] = x;
waveY[ 1 ][ i ] = amplitudeB * sin( 2.0 * PI * ( t/periodB - x/wavelengthB ) );
// 合成波
waveX[ 2 ][ i ] = x;
waveY[ 2 ][ i ] = waveY[ 0 ][ i ] + waveY[ 1 ][ i ];
}
// グラフソフトにデータを転送
setGraph2DData( graph, waveX, waveY );
// 時刻を加算(アニメーション速度をかけて変化のスピードを調整)
t += DT * speed;
// アニメーションウェイト(30ミリ秒待つ)
sleep( 30 );
}
exit(); // アニメーションループを脱出すると実行終了
}
// ==================================================
// 起動時に波のパラメータの初期値を訪ねて入力する関数
// ==================================================
void inputParameters() {
if ( confirm("波のパラメータを数値で入力しますか?") ) {
amplitudeA = input("波Aの振幅=", amplitudeA);
amplitudeB = input("波Bの振幅=", amplitudeB);
wavelengthA = input("波Aの波長=", wavelengthA);
wavelengthB = input("波Bの波長=", wavelengthB);
periodA = input("波Aの周期=", periodA);
periodB = input("波Aの周期=", periodB);
}
}
// ==================================================
// グラフソフトを起動して設定を行う関数
// ==================================================
void createGraphWindow() {
// 2Dグラフソフトを起動
graph = newGraph2D( 0, 0, 800, 600, "Graph Window" );
// 範囲の自動調整機能を無効化し、手動で範囲を指定
setGraph2DAutoRange( graph, false, false );
setGraph2DRange( graph, X_MIN, X_MAX, Y_MIN, Y_MAX );
// 線の幅などが記載されている設定ファイルを読み込む
setGraph2DConfigurationFile(graph, "./RinearnGraph2DSetting.ini");
// プロットオプションを設定
setGraph2DOption(graph, "WITH_POINTS", false);
setGraph2DOption(graph, "WITH_LINES", true);
// 背景色を白に設定
setGraph2DBackgroundColor( graph, 255, 255, 255, 255 );
// タイトルや座標軸ラベルの設定
setGraph2DLabel( graph, "x", "2つの正弦波(赤,青)と合成波(緑)" );
}
// ==================================================
// 設定画面を構築する関数
// ==================================================
void createSettingWindow() {
// ウィンドウの生成
window = newWindow( 0, 600, 800, 230, "Setting Window" );
// 時刻表示ラベルを生成して配置
timeLabel = newTextLabel( 10, 10, 200, 20, "" );
mountComponent( timeLabel, window );
// スライダーの左に振幅、周期、波長のラベルを生成して配置
int amplitudeLabel = newTextLabel( 45, 40, 100, 15, "A 振幅 (0〜1)" );
mountComponent( amplitudeLabel, window );
int omegaLabel = newTextLabel( 45, 60, 100, 15, "T 周期 (0.2〜5)" );
mountComponent( omegaLabel, window );
int lambdaLabel = newTextLabel( 45, 80, 100, 15, "λ 波長 (0.1〜4)" );
mountComponent( lambdaLabel, window );
// 振幅スライダー(範囲0.0〜1.0)を生成して配置
amplitudeSliderA = newHorizontalSlider( 150, 40, 300, 20, amplitudeA, 0.0, 1.0 );
amplitudeSliderB = newHorizontalSlider( 450, 40, 300, 20, amplitudeB, 0.0, 1.0 );
mountComponent( amplitudeSliderA, window );
mountComponent( amplitudeSliderB, window );
// 周期スライダー(範囲0.2〜5.0)を生成して配置
periodSliderA = newHorizontalSlider( 150, 60, 300, 20, periodA, 0.2, 5.0 );
periodSliderB = newHorizontalSlider( 450, 60, 300, 20, periodB, 0.2, 5.0 );
mountComponent( periodSliderA, window );
mountComponent( periodSliderB, window );
// 波長スライダー(範囲0.1〜4.0)を生成して配置
wavelengthSliderA = newHorizontalSlider( 150, 80, 300, 20, wavelengthA, 0.1, 4.0 );
wavelengthSliderB = newHorizontalSlider( 450, 80, 300, 20, wavelengthB, 0.1, 4.0 );
mountComponent( wavelengthSliderA, window );
mountComponent( wavelengthSliderB, window );
// スライダー値を表示するラベルを生成して配置
infoLabelA = newTextLabel( 155, 100, 300, 20, "" );
infoLabelB = newTextLabel( 455, 100, 300, 20, "" );
mountComponent( infoLabelA, window );
mountComponent( infoLabelB, window );
updateInfoLabel();
// 波Aと波Bの列を表すラベルを生成して配置
int columnLabelA = newTextLabel(280, 15, 200, 20, "波A");
int columnLabelB = newTextLabel(580, 15, 200, 20, "波B");
mountComponent( columnLabelA, window );
mountComponent( columnLabelB, window );
// アニメーション速度のラベルと調整スライダーを生成して配置
int speedLabel = newTextLabel( 10, 140, 140, 15, "アニメーション速度" );
mountComponent( speedLabel, window );
speedSlider = newHorizontalSlider( 150, 140, 400, 20, speed, 0.0, 1.0 );
mountComponent( speedSlider, window );
// 時刻リセットボタンを生成して配置
resetButton = newButton(600, 125, 150, 40, "時刻をリセット");
mountComponent( resetButton, window );
// 配置後にウィンドウを描画して表示内容を更新
paintComponent( window );
}
// ==================================================
// スライダー値を表示するラベルの内容を更新する関数
// ==================================================
void updateInfoLabel() {
string infoTextA
= "( A="
+ round(amplitudeA, 3, HALF_UP) // 振幅を小数点以下3桁に丸める
+ ", λ="
+ round(wavelengthA, 3, HALF_UP) // 波長を小数点以下3桁に丸める
+ ", T="
+ round(periodA, 3, HALF_UP) // 周期を小数点以下3桁に丸める
+ ")";
string infoTextB
= "( A="
+ round(amplitudeB, 3, HALF_UP) // 振幅を小数点以下3桁に丸める
+ ", λ="
+ round(wavelengthB, 3, HALF_UP) // 波長を小数点以下3桁に丸める
+ ", T="
+ round(periodB, 3, HALF_UP) // 周期を小数点以下3桁に丸める
+ ")";
setComponentString(infoLabelA, infoTextA);
setComponentString(infoLabelB, infoTextB);
paintComponent(infoLabelA);
paintComponent(infoLabelB);
paintComponent(window);
}
// ==================================================
// スライダーが動いた際に呼ばれる関数(イベントハンドラ)
// ==================================================
void onSliderMove(int id, float value) {
// 以下、スライダーに対応するグローバル変数に値を設定
if(id == amplitudeSliderA) {
amplitudeA = value;
}
if(id == amplitudeSliderB) {
amplitudeB = value;
}
if(id == periodSliderA) {
periodA = value;
}
if(id == periodSliderB) {
periodB = value;
}
if(id == wavelengthSliderA) {
wavelengthA = value;
}
if(id == wavelengthSliderB) {
wavelengthB = value;
}
if (id == speedSlider) {
speed = value;
}
updateInfoLabel();
}
// ==================================================
// ボタンを押した際に呼ばれる関数(イベントハンドラ)
// ==================================================
void onButtonClick(int id) {
// 時刻リセットボタンが押されたら時刻変数 t をリセット
if (id == resetButton) {
t = 0.0;
}
}
// ==================================================
// ウィンドウを閉じた際に呼ばれる関数(イベントハンドラ)
// ==================================================
void onWindowClose(int id) {
// アニメーションループを脱出して終了
continuesLoop = false;
}
// ==================================================
// グラフ画面を閉じた際に呼ばれる関数(イベントハンドラ)
// ==================================================
void onGraph2DClose(int id) {
// アニメーションループを脱出して終了
continuesLoop = false;
}
以上です。大体300行ちょっとの規模の短いコードですね。 各部で行っている処理はコード内のコメントの通りですが、 以下では先頭から順を追って、もう少し詳しく説明します。
基本的には、前回の「 正弦波のアニメーション表示 」のコードと非常によく似ていて、 波の数が増えたので少し拡張されているだけです。 なので、コードの基本的な流れについては、まず前回のコードをご参照ください。
以下では、前回から変わっている部分を中心に、ピックアップして解説していきます。
変数の宣言
先頭から続く変数の宣言部では、基本的には前回と同じで、 そこから波のパラメータや操作用スライダーなどの変数が、 波Aと波Bの2通りぶん用意されるようになっただけです。
ただし、波のデータをグラフソフトに渡すための、座標値を格納する配列については、 1次元だったのが2次元配列になっています:
// グラフに波のデータを渡すための座標値配列
double waveX[ 3 ][ N ]; // X座標の配列 / 波A,波B,合成波の合計3系列 × 座標点数
double waveY[ 3 ][ N ]; // Y座標の配列 / 波A,波B,合成波の合計3系列 × 座標点数
これは、今回は複数系列のデータをグラフに渡してプロットする必要があるためで、 左端の次元が、系列を区分する次元になります。 今回は波A、波B、合成波の3つの系列に分けてデータをプロットするため、左端次元の要素数は 3 になっています。
右端の次元は前回と同様、座標点についての次元です。1系列あたり N 個の点を線で結ぶので、要素数は N になっています。
main 関数内、波のデータを座標値配列に格納してグラフに渡す部分
続いて main 関数のアニメーションループ内で、波のデータを座標値配列に格納してグラフに渡す部分です。
// グラフソフトに渡す点列データの座標を計算
for( int i=0; i<N; i++ ) {
double x = X_MIN + i * DX; // i番目の点のx座標値
// 波A
waveX[ 0 ][ i ] = x;
waveY[ 0 ][ i ] = amplitudeA * sin( 2.0 * PI * ( t/periodA - x/wavelengthA ) );
// 波B
waveX[ 1 ][ i ] = x;
waveY[ 1 ][ i ] = amplitudeB * sin( 2.0 * PI * ( t/periodB - x/wavelengthB ) );
// 合成波
waveX[ 2 ][ i ] = x;
waveY[ 2 ][ i ] = waveY[ 0 ][ i ] + waveY[ 1 ][ i ];
}
// グラフソフトにデータを転送
setGraph2DData( graph, waveX, waveY );
ここはアニメーションループの内側なので、ある時刻(時刻変数 t )の瞬間におけるグラフを1枚描く処理だと思ってください。 これがパラパラ漫画の要領で、t を小刻みに増やしながら繰り返し実行され、その結果としてグラフがアニメーションします。
さて、波Aと波Bについては前回と同じ事をそのまま2つぶんやってるだけです。 おさらいすると、X 軸方向に小刻みに刻んだ各地点において、正弦波の式:
\[ y = A \sin 2 \pi \bigg( \frac{t}{T} - \frac{x}{\lambda} \bigg) \] に基づいて Y 座標を求め、各点のX/Y座標値をそれぞれ配列に格納しています。 すると、グラフソフトがその各点を線で結んでくれるのでしたね。それに続くのが合成波の部分で、同様に小刻みに刻んだ各点のX/Y座標値を配列に格納しています。 その際、各点の Y 座標の値を求めるのに、波Aと波Bにおける各点のY座標を単純に足しているだけです。 こんな単純な計算で合成波の形が求まるのは、 波について学ぶ際に例に挙げられるような普通の波においては、 波の重ね合わせの原理 ―― まさに波の値を単純に足したものが合成波の値になるという原理 ―― が日常スケールで精度よく成り立つおかげです。
逆に言うとこのプログラムでは、波の重ね合わせの原理が完璧に成り立つ、理想的な場合を前提としています ※。
※ もちろん、成り立たない場合もあって、その場合はこんな単純な計算にはなりません。 そういう場合は、各時刻で波Aと波Bの形から合成波を求めるというよりも、 合成波の形を最初に決めた上で、時間発展の微分方程式を数値的に解いて、その後の動きをシミュレーションする事になるでしょう。
その他の部分
その他の部分については、前回のコードの単純な拡張で、 画面上のスライダーなどが波2本ぶんに増えたりしているだけです。 特に引っかかりそうな改変を行っている部分は無いと思います。
コード内容は以上です。
ライセンス
このVCSSL/Vnanoコード( 拡張子が「.vcssl」や「.vnano」のファイル )は実質的な著作権フリー(パブリックドメイン) である CC0 の状態で公開しています※。 記事中にC言語/C++/Java言語などでのサンプルコードが掲載されいてる場合は、それらについても同様です。 そのままでのご利用はもちろん、改造や流用などもご自由に行ってください。
※ ただし、このコードの配布フォルダ内には、ダウンロード後すぐに実行できるように、 VCSSLの実行環境も同梱されており、そのライセンス文書は「 License 」フォルダ内に同梱されています (要約すると、商用・非商用問わず自由に使用できますが、使用の結果に対して開発元は一切の責任を負いません、といった具合の内容です)。 配布フォルダ内の各構成物の一覧やライセンスについては「 ReadMe_使用方法_必ずお読みください.txt 」をご参照ください。
※ Vnano の実行環境については、別途スクリプトエンジンのソースコードも一般公開しており、 何らかのソフトウェア内に組み込んでご利用いただく事も可能です。詳細はこちらをご参照ください。
この記事中の商標などについて
- OracleとJavaは、Oracle Corporation 及びその子会社、関連会社の米国及びその他の国における登録商標です。文中の社名、商品名等は各社の商標または登録商標である場合があります。
- Windows は、米国 Microsoft Corporation の米国およびその他の国における登録商標です。この記事は独立著作物であり、Microsoft Corporation と関連のある、もしくはスポンサーを受けるものではありません。
- Linux は、Linus Torvalds 氏の米国およびその他の国における商標または登録商標です。
- その他、文中に使用されている商標は、その商標を保持する各社の各国における商標または登録商標です。
|
Vnano版 | ローレンツ方程式を数値的に解くプログラム |
|
|
|
ローレンツ方程式を4次ルンゲ=クッタ法によって解き、グラフ描画用のデータを出力するプログラムです。 |
|
波の干渉(面上の円形波)のアニメーション表示 |
|
|
|
面上の円形波が干渉する様子を、パラメータを操作しながらアニメーションで見られるプログラムです。 |
|
円形波のアニメーション表示 |
|
|
|
振幅・波長・周期をスライダ―で操作しながら、円形波のグラフをアニメーションで見られるプログラムです。 |
|
波の干渉(線上の正弦波)のアニメーション表示 |
|
|
|
線上(1次元の)の正弦波が干渉する様子を、パラメータを操作しながらアニメーションで見られるプログラムです。 |
|
正弦波のアニメーション表示 |
|
|
|
振幅・波長・周期をスライダ―で操作しながら、正弦波のグラフをアニメーションで見られるプログラムです。 |
|
凹レンズを通過する波のシミュレーション |
|
|
|
凹レンズ形状の高密度媒質を通過する、波のシミュレーションです。 |
|
凸レンズを通過する波のシミュレーション |
|
|
|
凸レンズ形状の高密度媒質を通過する、波のシミュレーションです。 |
|
乱雑な密度分布における波のシミュレーション |
|
|
|
密度分布が乱雑な媒質中における、波の伝播のシミュレーションです。 |
|
ローレンツアトラクタ(ファイル出力版) |
|
|
|
4次精度ルンゲ=クッタ法により、ローレンツアトラクタを求めるプログラムです。 |
|
波の屈折のシミュレーション |
|
|
|
密度の異なる領域を、波が屈折しながら通過するシミュレーションです。 |
|
力学アルゴリズムによる波のシミュレーション(面上の波) |
|
|
|
媒質をバネと格子点で近似し、力学的なアルゴリズムで動かす事による、波のシミュレーションです。 |
|
手動で波を発生させるシミュレーション |
|
|
|
スライダーをマウスで動かす事により、波を発生させるシミュレーションです。 |
|
力学アルゴリズムによる波のシミュレーション(線上の波) |
|
|
|
媒質をバネと格子点で近似し、力学的なアルゴリズムで動かす事による、波のシミュレーションです。 |
|
二重振り子のシミュレーション |
|
|
|
ラグランジュ方程式を用いた、二重振り子のシミュレーションです。 |
|
ローレンツアトラクタ(GUI版) |
|
|
|
4次精度ルンゲ=クッタ法により、ローレンツアトラクタを求めるプログラムです。 |