円形波のアニメーション表示

振幅・波長・周期などのパラメータに基づいて、円形波をアニメーションで描画するVCSSLプログラムです。

前回 と 前々回 は、線の上、つまり1次元的な媒質上を伝わる 正弦波 のアニメーションを扱いました。 今回はその延長で、面の上、つまり2次元的な媒質上を伝わる波を扱ってみましょう。 具体的には、波源から同心円状に広がる円形波をアニメーションで表示してみます。

[ 関連記事 ]

• 前回： 波の干渉（線上の正弦波）のアニメーション表示
• 前々回： 正弦波のアニメーション表示

スポンサーリンク

---

使用方法

ダウンロードと展開（解凍）

まず、PC（スマホは未対応）で上の画面の「 ダウンロード 」ボタンを押してください。 するとZIP形式で圧縮されたファイルがダウンロードされます。

その後、ZIPファイルを右クリックして「すべて展開」や「ここに展開」などで展開（解凍）してください。 展開が成功すると、ZIPファイルと同じ名前のフォルダができ、その中にZIPファイルの中身が入っています。

» 展開がエラーで止まってしまう場合や、ファイル名が文字化けしてしまう場合は…

プログラムの起動

Windows をご使用の場合

上記でZIPファイルを展開したフォルダ内にある、以下のバッチファイルをダブルクリック実行してください：

もしプログラムを書き変えながら使いたい場合は、代わりに「 VCSSL_Editor__プログラム編集はこちら.bat 」を実行してください。

正常に起動できると、初回のみ、Java実行環境を入手するか等を尋ねられるので、適時答えて済ませると、プログラムが起動します。 2回目以降はすぐに起動します。

» うまく起動できずにエラーになってしまう場合は…

Linux 等をご使用の場合

ZIPファイルを展開したフォルダ内へコマンドライン端末で cd して、以下の通り入力して実行してください：

» javaコマンドが使用できない等のエラーが表示される場合は…

起動後の画面

起動すると、まず波のパラメータを数値入力するか尋ねられます。 特に「ぴったりこの値の波長にしたい」などの必要が無ければ、「いいえ」でスキップして構いません。

その後、グラフ画面とパラメータ設定画面が立ち上がります。

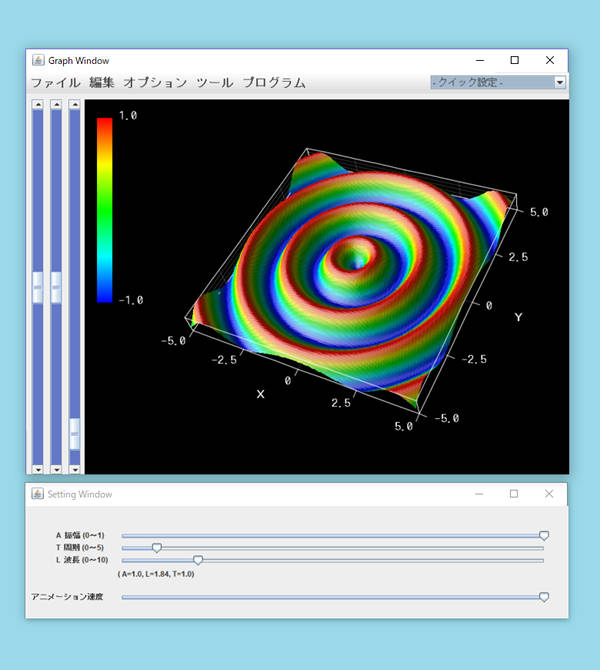
グラフ画面では、円形波がアニメーション表示されます。 パラメータ設定画面では、波の波長や振幅、周期などの値をスライダーで操作できます。

ウィンドウを閉じると、プログラムの実行が終了します。

題材解説

円形波は、波源と呼ばれる振動源の動きが、周囲の媒質へ同心円状に伝わっていく事で起こります。

お風呂などで、水面をそっと指で触れると、実際にそこから円形に波が広がっていくのが見られるかと思います。 さらに、指を水面に対して垂直に振動させると、同心円状の波が連続的に広がっていきます（この場合は指が波源です）。

ここでは単純のため、波の各点は、（振幅を含めて）波源と全く同じ動きを、波源からの距離に応じて少し遅れながら行っていると仮定しましょう。 そして、波源は単振動（調和振動）をしているものとします。 そのように仮定すると、波を波源を面で切った断面は、 前々回に扱った正弦波となります。

より具体的には、面上のある点 \( (x,y) \) における波源からの距離を \( r \) として :

\[ r = \sqrt{x^2 + y^2} 　　　 (1) \]

その点での波の振動の値を \( z \) とすると、それは

\[ z = A \sin 2 \pi \bigg( \frac{t}{T} - \frac{r}{\lambda} \bigg) 　　　 (2) \]

と表す事ができます※。 これは 前々回 見た正弦波の式の \( x \) が \( r \) に置き換わっただけですね。 ただし、波源の位置 \( r = 0\) を挟んだ反対側で、波の進む向きが逆転する（波は波源から離れる向きに進む）事には注意が必要です。 \( A \) は振幅、\( \lambda \) は波長、\( T \) は周期で、これも 前々回 と同じなので、詳しくはそちらの説明をご参照ください。

---

スポンサーリンク

---

コード解説

このプログラムのコードはVCSSLで記述されています。 ここではそのコード内容について簡単に解説します。 VCSSLはC系の単純な文法の言語なので、C言語などに触れた事のある方なら簡単に読めると思います。

グラフの範囲などを変えたり、色々と改造したいといった場合などは、 プログラムのコード「 CircularWave.vcssl 」をテキストエディタで開いて改造してください。 スクリプト言語なので、コンパイラなどの別ソフトは不要で、コードを書き換えるだけでOKです。

コード全体

まずは、コード全体を見てみましょう。

以上です。大体250行程度の規模の短いコードですね。 各部で行っている処理はコード内のコメントの通りですが、 以下では先頭から順を追って、もう少し詳しく説明します。

基本的には、前々回の「 正弦波のアニメーション表示 」のコードと非常によく似ていて、 波のデータの次元が増えたのと、表示する2Dグラフが3Dグラフになっただけです。 なので、コードの基本的な流れについては、まず前回のコードをご参照ください。

以下では、前々回から変わっている部分を中心に、ピックアップして解説していきます。

変数の宣言

先頭から続く変数の宣言部では、基本的には前々回と同じですが、 Z方向の次元が新たに増えたので、それに関連する変数が増えています。

waveX / waveY / waveZ などは、グラフに波のデータを渡すために、波が起こる面上を細かく刻んだ各点の座標値を格納する配列です。 前々回では、波は線の上（X軸上）で起こっていたので、それを単純に刻んだ1次元配列でした。 今回は、波は面の上（X-Y平面上）で起こるので、それをメッシュ状に刻んだ2次元配列になっています。

メッシュはX軸方向とY軸方向にそれぞれ N 個の格子点があるように刻み（つまり区間数は N-1 ）、その区間幅はそれぞれ DX および DY です。

main 関数

続いて main 関数です。

ここも基本的には前々回と同じで、 while( continuesLoop ) { 〜 のアニメーションループ内で、 時刻を小刻みに進めながら、波の起こる面上を細かく刻んだメッシュの格子点上で、波の値を求めて配列に格納し、 それをグラフに渡して描画してもらっています。

重要なのが、波の値を求めて配列に格納している部分：

で、この 72行目と76行目は、このページの冒頭で登場した (1) - (2) 式：

\[ r = \sqrt{x^2 + y^2} 　　　 (1) \] \[ z = A \sin 2 \pi \bigg( \frac{t}{T} - \frac{r}{\lambda} \bigg) 　　　 (2) \]

をそのままプログラムのコードの形にしたものです。 つまり今回の処理は、パラパラ漫画の要領で時刻 t を小刻みに進めながら、(2) 式を3Dグラフに連続で描かせてアニメーションしている内容になっています。

コード内で本質的に重要なのはここまでで、残りの部分はグラフ周りの設定や、GUI画面の構築などの枝葉の処理です。 グラフ周りでは、VCSSLでは2Dグラフと3Dグラフを同じ感覚で扱えるようになっているため、 呼び出している関数名の「2D」が「3D」になっているくらいで、やっている事や流れは前々回とほとんど変わりません。 GUI構築やイベント処理に関しても、前々回とほぼ同じです。

コード内容は以上です。

ライセンス

このVCSSL/Vnanoコード（ 拡張子が「.vcssl」や「.vnano」のファイル ）は実質的な著作権フリー（パブリックドメイン) である CC0 の状態で公開しています※。 記事中にC言語/C++/Java言語などでのサンプルコードが掲載されいてる場合は、それらについても同様です。 そのままでのご利用はもちろん、改造や流用などもご自由に行ってください。

※ ただし、このコードの配布フォルダ内には、ダウンロード後すぐに実行できるように、 VCSSLの実行環境も同梱されており、そのライセンス文書は「 License 」フォルダ内に同梱されています （要約すると、商用・非商用問わず自由に使用できますが、使用の結果に対して開発元は一切の責任を負いません、といった具合の内容です）。 配布フォルダ内の各構成物の一覧やライセンスについては「 ReadMe_使用方法_必ずお読みください.txt 」をご参照ください。

※ Vnano の実行環境については、別途スクリプトエンジンのソースコードも一般公開しており、 何らかのソフトウェア内に組み込んでご利用いただく事も可能です。詳細はこちらをご参照ください。

この記事中の商標などについて

• OracleとJavaは、Oracle Corporation 及びその子会社、関連会社の米国及びその他の国における登録商標です。文中の社名、商品名等は各社の商標または登録商標である場合があります。
• Windows は、米国 Microsoft Corporation の米国およびその他の国における登録商標です。この記事は独立著作物であり、Microsoft Corporation と関連のある、もしくはスポンサーを受けるものではありません。
• Linux は、Linus Torvalds 氏の米国およびその他の国における商標または登録商標です。
• その他、文中に使用されている商標は、その商標を保持する各社の各国における商標または登録商標です。