角度の「度」とラジアンとを相互変換し、図示もするツール

このプログラムは、角度における「度」をラジアンに変換したり、逆にラジアンを度に変換したりできるGUIツールです。 対応する角度を、図として表示する機能も付いています。

スポンサーリンク

---

使用方法

ダウンロードと展開（解凍）

まず、PC（スマホは未対応）で上の画面の「 ダウンロード 」ボタンを押してください。 するとZIP形式で圧縮されたファイルがダウンロードされます。

その後、ZIPファイルを右クリックして「すべて展開」や「ここに展開」などで展開（解凍）してください。 展開が成功すると、ZIPファイルと同じ名前のフォルダができ、その中にZIPファイルの中身が入っています。

» 展開がエラーで止まってしまう場合や、ファイル名が文字化けしてしまう場合は…

プログラムの起動

Windows をご使用の場合

上記でZIPファイルを展開したフォルダ内にある、以下のバッチファイルをダブルクリック実行してください：

もしプログラムを書き変えながら使いたい場合は、代わりに「 VCSSL_Editor__プログラム編集はこちら.bat 」を実行してください。

正常に起動できると、初回のみ、Java実行環境を入手するか等を尋ねられるので、適時答えて済ませると、プログラムが起動します。 2回目以降はすぐに起動します。

» うまく起動できずにエラーになってしまう場合は…

Linux 等をご使用の場合

ZIPファイルを展開したフォルダ内へコマンドライン端末で cd して、以下の通り入力して実行してください：

» javaコマンドが使用できない等のエラーが表示される場合は…

起動後

起動すると、下図のようなウィンドウが表示されます。

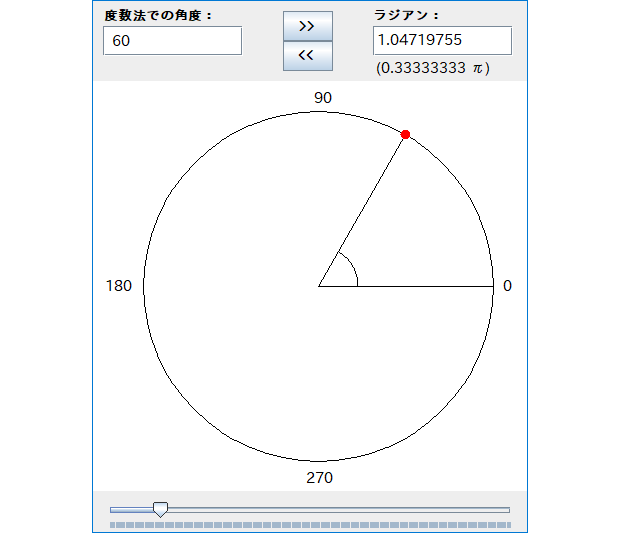
このウィンドウ上で、以下のように、角度の変換操作を行えます：

「度」からラジアンへの変換

画面左上の「度数法での角度：」の欄に、角度の「度」の値や計算式※を入力して、「 >> 」ボタンを押します。 すると「ラジアン：」の欄に、変換されたラジアン値が表示されます。

ラジアンから「度」への変換

「ラジアン：」の入力欄に、角度のラジアン値や計算式※を入力してて、「 << 」ボタンを押します。 すると「度数法での角度：」の欄に、変換された「度」の値が表示されます。

なお、上のどちらでも、対応する角度が図で表示されます。 加えて、図の下にあるスライダーで角度を操作すると、それに対応する「度」の値とラジアン値が、自動的にそれぞれの欄に表示されます。

---

スポンサーリンク

---

題材解説

角度を表す2つの単位：「度」と「ラジアン」

さて、今回のテーマについての解説（雑談？）です。既に上でも説明した通り、今回のプログラムは 角度の変換 を行うものです。 具体的には、角度を表す2つの単位である、「度」と「ラジアン」との間の変換を行います。

さてこの「ラジアン」、数学とかで習った事がある人も多いと思うんですが、それでも「なんか名前だけ聞いたことある」くらいで、詳細は忘れてしまっている人が（一般には）多いんじゃないでしょうか。 だって、日常生活ではラジアンはほとんど使われませんよね。もっぱら「45度」とかの「度」を使います。

でも、高校数学とかで出てきた通り、数学や理論寄りの解析が関わるような所では、角度といえばラジアンです。 逆に、「 度、どこ行ったの…？ 」って感じになります。 「ややこしいし、どっちかに統一してよ！」って思うかもしれません。

でも、まあ逆に統一されずに両方生き残っているという事は、やっぱりそれぞれ生き残る理由があるわけですよね。 という事で今回の記事では、そのあたりを踏まえて、それぞれの量を少し掘り下げてみましょう。

実用面で便利な「度」（度数法）

まずは一番なじみ深い「度」という単位。30度とか45度とか。表現法としては「度数法（どすうほう）」と呼ばれたりもします。

これはもう非常によく知られている通り、一周ぐるっと回る角度を360度としたものです。つまり 1周の360分の1を単位「1度」とする量ですね。

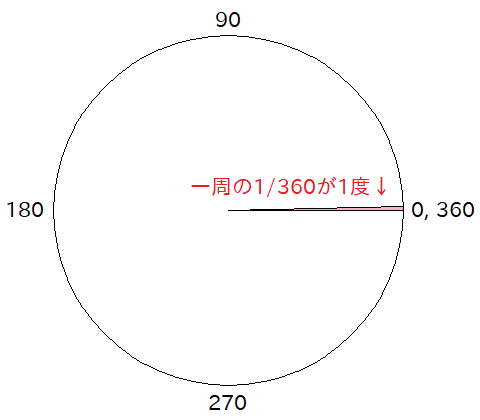
で、これは結構有名なんですが、実はこの「360」っていう数字がかなり優れもので、いろんな数で綺麗に割り切れます（時間で登場する 60 とかもそう）。 具体的に例を挙げると、1、2、3、4、5、6、(7は無理、おしい！)、8、9、10... で割り切れます。

という事は、一周の1/2の角度（=180度）、1/3の角度（=120度）、1/4の角度（=90度）、1/5の角度（=72度）、... といった、よく登場しそうな角度が、少ない桁数の（かつ分数ではない）簡単な数字で書けるという事になります。

これは実用面で非常にうれしい性質ですよね。確かにうれしい。最初に導入した人えらい。

どっちかというと理論寄りの所でよく出くわす「ラジアン」

さて、次は「ラジアン」という単位です。こちらは表現法としては「弧度法（こどほう）」と呼ばれます。 単位の記号は rad と書いて「ラジアン」と読みます。

弧度法そのもののの説明は Wikipedia とかにある ので、ここで長い説明を入れるよりそっちを見てもらった方がいいです。 そもそもこの記事に辿り着く人は知ってそうですし。一応ラフに描いた概念図を置いておくと下図です。

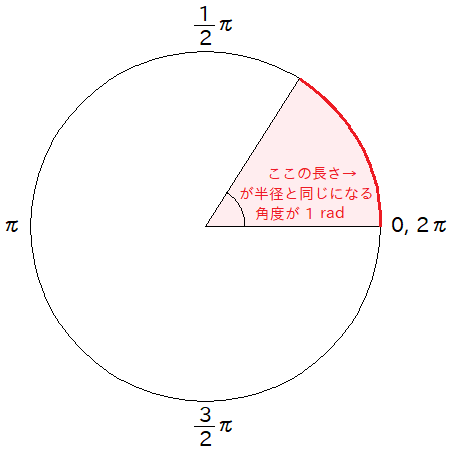
で、上の通り弧度法では、半径と円弧の長さとの比※によって角度を扱います。

ラジアンに慣れない方は、定義から忠実に追うと少しややこしいかもしれません（1 rad の説明とか）。 ただ、結果的には要するに 1周ぐるっと回ると \( 2 \pi \) rad になる、といったような量になります。 つまり度数法での 360 が弧度法では \(2 \pi\) になるような。なので、度とラジアンは以下のように変換できます：

\[ \rm{ラジアン単位での角度} = \frac{2 \pi}{360} \times \rm{度単位での角度} \] \[ \rm{度単位での角度} = \frac{360}{2 \pi} \times \rm{ラジアン単位での角度} \]

さて、理論とか解析とかで日常的に登場する、三角関数の \( \sin x \) とか \( \cos x \) のパラメーターは、\( x \) をそのまま角度と見なす場合、ラジアン基準（弧度法）で定義される事がとても多いです（後で掘り下げます）。

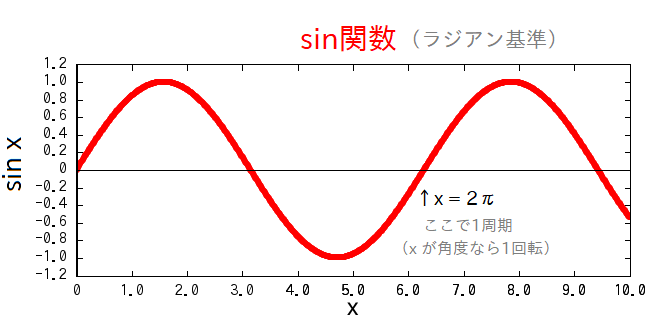
一応、実用色が濃い場面や図形メインの場面とかだと、sin や cos のパラメータが「度」にされる事もあるようですが（見かけます）、しかし微積分とか多項式近似とかでほじくり回すような理論面だと普通ラジアン基準です。

また、図形とか角度とかが全く関係ない場面でも、sin や cos は複素数とか振動/周波数関連とかの分野で、まるで空気の成分のように至る所で出てきます。 そういった際に、パラメータ \(x\) を角度的なもの（位相）だと思うと、それは sin や cos の周期 \( 2 \pi \) から、必然的にラジアン基準に一致する形（一周ぐるっと回ると\(2 \pi\)）になります。

なので、ちょっと理論や解析の方向に足を突っ込むと、ラジアン基準だらけになり、実用との境界のあたりで変換が必要になるわけですね（具体的に角度を測って式に突っ込む時とか）。

余談：
\( 2 \pi \) というのは突拍子もなく思えるけど、実は sin / cos 的には結構自然な値だよという話

で、ラジアンの現実的な重要性（よく出くわす）については以上の通りなのですが、以下のような疑問が残る方も多いんじゃないでしょうか：

といった具合です。これはつまり言い換えると

というのとほぼ同じ事ですね。実はこれは、筆者自身が一時期疑問に思っていた事でもあります。

まあ、実際のところ筆者はラジアンの歴史的経緯とか普及の過程とかを全然知らないので、正確な理由は分かりません。 ただ、個人的に昔あれこれ考えた際に、「 少なくとも \( 2 \pi \) ってのは sin や cos にとってはそんなに突拍子もない or 偶然の産物ではなく、むしろ自然な値だなあ 」と思う程度には納得できたので、その内容を以下に書き留めておきます。

あくまでも単に、筆者なりの視点なので、その点はご留意ください。

◇

まず sin や cos 関数自体についてなんですが、これは歴史的ルーツとか教育での習い方とかでは、幾何学的（＝図形的）な意味から導入されますよね。 なので \( \sin x \) の \( x \) は角度、っていうイメージが頭にしみ込んでます。

でも、これらを数学関数として定義するという事は、つまり「 \( x \) という実数を、他の実数に対応づける、抽象的な存在 」として定義するという事ですよね。 その対応づけ方が、ルーツとして幾何学や角度から出発しているというだけで。 なので、定義された後に \( x \) に何を突っ込もうが（好きな数字でも何でも）、単にそれに対応する値が求まるだけで、「 \( x \) は角度です 」って縛られてるわけではない。\( x \) はただの実数なわけです。

という事で、ここで「\( x \)は角度」というイメージは一旦置いてしまいましょう。どうせ実用時はスケーリングとか単位変換とか絶対必要になるので、そういうのは適当に係数とか挟んで使う側でやってほしい、といった具合で。

数学的にはそういうのは置いておいて、純粋に最も本質的っぽい形で \( \sin x \) とかを定義したいはず。 という立場からすると、定義時に \( x \) をスケーリングすると周期が変わるけど、sin や cos にとって一番本質的っぽい周期になるように定義したいですよね。では、その適切な周期って何でしょう？

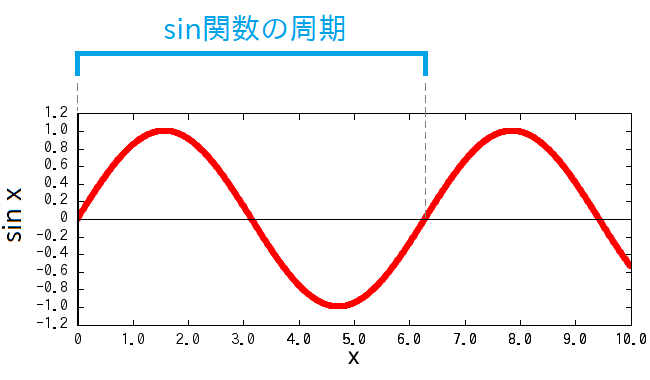
それを考えるために、幾何学や角度から離れて、sin や cos のもう一つの側面に目を向けてみます。 具体的には、少し天下り式ですが、周期 \( 2 \pi \) の sin や cos 関数 を、\( x \) の多項式で表してみます（マクローリン展開）：

\[ \sin x = x^1 - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} - ... = \sum_{n = 0}^{\infty} \frac{(-1)^n x^{2n + 1}}{(2 n + 1)!} \] \[ \cos x = x^0 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} - ... = \sum_{n = 0}^{\infty} \frac{(-1)^n x^{2n}}{(2 n)!} \]

非常に規則的で、とても整った多項式ですね。 なんか、この式をもう一つの sin 関数や cos 関数の定義と思いたくなるくらいの整いっぷりです。 まさに sin や cos の正体を掴んでいる！って感じがしませんか？ 筆者はします。

特にすごいのは、上の多項式のどこにも \( 2 \pi \) なんて数は入っていない事です。 むしろ必要最小限の要素のみで構成されている。分母の階乗（2!とか）はマクローリン展開/テイラー展開由来で本質的に出てくるので、それを除けば、各項の \(x^n\) の部分に符号しかかかってない。 絶対 \(2 \pi\)とか入ってきそうな気がするのに、逆になんと、数値的な係数が何も入ってこない。

にも関わらず、上の多項式はしっかり周期 \(2 \pi\) の sin 関数や cos 関数を表しているんですよね。 言い換えると、「 もし仮に、上の整った多項式から出発して sin 関数や cos 関数を定義したら、角度どうこうの議論が全く無くても、自然と周期は \(2 \pi\) になる 」という事です。

上の多項式は、解析においてとても重要です。各項に、変なスケーリング由来の係数とか変形とかは入ってきてほしくなく、明らかにこの形が最も整っています。 そして周期を \( 2 \pi \) からいじると（つまり x に係数がかかった際に等価な値になるよう sin 関数を再定義すると）、上の最も整った形からは崩れてしまいます。 とすると、周期は \( 2 \pi \) でよかったーってなるわけです。

さて、この段階で、改めて \( x \) を角度と見なして、sin と cos の周期から角度の単位を作れば、\( 2 \pi \) で一周すべきなので、それはまさにラジアンに一致するわけですね。 まあ実際はどういう経緯でそうなったのか全く知りませんが、少なくとも \(2 \pi\) やラジアンといった量は、sin や cos と本質的にマッチしている事は感じ取れます。

余談の余談：指数関数との関係とか

ところで、上で触れたのとほぼ同じような話は、指数関数とネイピア数 \( e \)（自然対数の底） についてもできます。

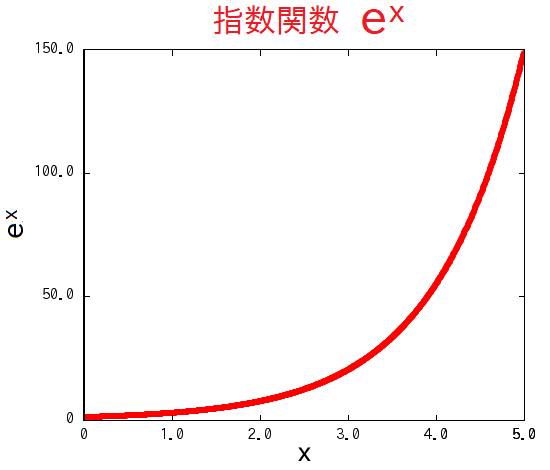
指数関数というと、 \( e^x \) こそが「主役」で、他の \( a^x \) とか \( b^x \) とかは「なんかその周辺の一種」みたいな感じですよね。 でも \( e \) って、\( \pi \) と並び称され得る無理数で、値としては 2.7182818... と、めっちゃ中途半端かつ延々と続きます。 なんでそんな中途半端な、一見すると突拍子もない値が、指数関数においてそんな重要そうな扱いなの？ って思いますよね。

あれ？でもこれってなんか、さっきの sin や cos と \( 2 \pi \) の話と似てません？ という事で、\( e^x \) も多項式で表してみましょう：

\[ e^x = x^0 + x^1 + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + ... = \sum_{n=0}^{\infty} \frac{x^n}{n!} \]

と、この通り、やはり非常に整った多項式になりましたね。これもまさに、指数関数の本質を掴んでそうな感じです。 底が \( e \) ではない \( a^x \) や \( b^x \) では、ここまで綺麗にはなりません（各項にべき乗の係数が入ってきます）。

なので逆に、仮に上の最も整った多項式になるやつを指数関数の主役と呼ぶなら、その底は必然的に \( e \) = 2.7182818... になる、と言えます。 登場の仕方までさっきの \( 2 \pi \) と同じですね。

多項式の各項を見比べても、sin 関数や cos 関数と \(e^x\) は、なんかだ非常に似ている、親戚みたいな雰囲気を感じ取れます。 そこで指数関数のパラメータを複素数の範囲に拡張し、上の \( e^x \) の多項式の \( x \) を \( i x \) （\(i\)は虚数単位）で置き換えると、以下のような関係が導かれます：

\[ e^{i x} = \cos x + i \sin x \]

と、この通り、イメージ的には全然関係なさそうな sin や cos と \( e^x \) が、実は複素数まで拡張すると完全に繋がってるんですよ。 これも複素数が出てくる場面ではめちゃくちゃ重要な関係で、よく登場するというか、重要すぎて逆にもう登場とかいう次元ではない感じのやつです。 むしろもう複素数の本質の一部でしょう、みたいな。

これに人為的な「360」とかに由来する数字とか変形とかがわらわら入ってくるのは、やはりめっちゃ嫌で、このシンプルさの極限のような形であってほしいわけです。 そうなるようにスケールを決めてほしい。じゃないと、かの有名なオイラーの等式もぶち壊しですし。

となるとやっぱり、それを実現している \(e\) とか \(\pi\) っていう2つの数は、なんかこの世の本質的な構造を司っているような偉大な存在っぽくて、なのでほら、ラジアンも非常にありがたく思えてきません？（疲れた）

コード解説

テーマの説明は以上で、ここからは、今回のプログラムのコードを解説します。 このプログラムのコードはVCSSLで記述されています。

内容を書き変えて改造したい場合には、 プログラムのコード「 RadianConverter.vcssl 」をテキストエディタで開いて改造してください。 スクリプト言語なので、コンパイラなどの別ソフトは不要で、コードを書き換えるだけでOKです。 VCSSLはC系の単純な文法の言語なので、C言語などに触れた事のある方なら簡単に読めると思います。

コード全体

コード全体は以下の通りです。

以上です。大体300行にちょっと足りない程度の、そこそこの長さのコードですね。

詳細はコード内コメントに書いてある通りなんですが、 以下では、各部の概要をざっと追いながら説明しています。

先頭領域

まずは先頭から数行の領域です：

最初の「 coding UTF-8 」の行は、コードのファイルの文字コードが UTF-8 である事を明示しています。 必須では無いのですが、書いておくと文字化けを防げます。

続く「 import ... 」の行が連なる箇所では、使用するライブラリを読み込んでいます。 重要なのは「 GUI 」と「 Graphics2D 」ライブラリです。 前者はウィンドウやボタンなどの「画面周り」の機能を提供し、後者は2D描画の機能（今回は角度を図示するために使用）を提供します。

上述ら2つのライブラリは、単に仕様書だけだと使い方が分かり辛いので、以下のように開発ガイドがあります：

• GUI開発ガイド
• 2DCG開発ガイド

GUIや描画処理の流れを詳しく知りたい方は、上記を併せてご参照ください。

定数類

次に、ウィンドウのサイズなどを定数（const 付き変数）として定義しています：

これらの値はコード内で何度も出てくるので、数字をベタ書きするよりは、 こうしてコードの頭に書いておいた方が行儀が良い… はずなんですが、 GUIは細かい微調整とか多くて、今回も結局面倒になって随所に数字をベタ書きしてしまってるので、 ここの数値を変えても結局あちこちレイアウトの微調整が必要になり、実態としては全く行儀よくなってないです。

まあ「せめて画面サイズくらいはベタ書きせずに…」みたな後ろめたさの残り香みたいな感じですね。 一応そういう意識が無いわけではない、という気持ちの表明というか。まあ即席で書いて終わりのコードではあるあるです（筆者には）。

グローバル変数類

次に、定数（const）でないグローバル変数類を宣言しています。

VCSSLでは、GUI部品や描画関連リソース類は、生成時にID番号が割り振られ、それを使って操作/管理するようになっています。 そういったIDは、あちこちの関数内から参照するので、上記のグローバル変数に格納して使います。

「NULL」という値で初期化しているのは、IDの格納忘れに対する保険みたいな意図で、こうするとそのまま使った際に確実にエラーで落ちます（なので気づく）。

main 関数

宣言/定義類はここまでで、これ以降は処理類です。まずは main 関数です：

この main 関数は、他の言語と同じで、プログラムを実行すると自動で呼び出されます。 従ってここでは、起動後に必要な、GUIの構築などの処理を行っています。

中で呼んでいる initializeGUI 関数とか updateDisplay 関数とかは、コード内で後で宣言しています。

角度の「度」とラジアンの変換関数

その後には、今回のテーマとしては一番重要な、角度の「度」とラジアンを変換する関数を宣言しています。 これらは、あちこちの関数内の処理で呼ばれます。

上記の degreeToRadian 関数は、度（degree）の値を引数に取って、ラジアン値（radian）に変換して返します。

そのためにまず、「 1度あたり何ラジアンか 」という換算比率を、変数 radianPerDegree として求めています。 円をぐるっと一周、つまり360度回ると \(2 \pi\) ラジアンなので、その比率は：

\[ \rm{radianPerDegree} = \frac{2 \pi}{360} \]

ですね。約分して \( \pi / 180 \) にしてもいいのですが、今回のプログラムの性質上、直球で書いたほうがよさそうな気がしたので、上記をそのままコードにしています。 で、上の換算比率に「度」の値をかけると、ラジアンが求まるので、それを戻り値として返しています。

もう一つの radianToDegree 関数は、上記と全く逆に、ラジアン値（radian）を引数に取り、それを度（degree）の値に変換して返します。 処理の感覚は上とほぼ同じで、換算比率が逆転するだけです：

\[ \rm{degreePerRadian} = \frac{360}{2 \pi} \]

上の換算比率にラジアンを書けると「度」が求まるので、それを返しています。

ウィンドウやGUI周りの構築処理

その後には、ウィンドウを含むGUI関連の構築を行う initializeWindow 関数を宣言しています。これは先ほどの main 関数内から呼んでいましたね。なので、プログラム起動時に実行されます。

ここはかなり場当たり的な処理で、文章で詳しく説明してもどうしようもないので、コード内のコメントをご参照ください。 延々とGUI部品を生成しては配置して…を繰り返している感じです。

なお、GUI部品の生成と配置などの扱いについては、下記ガイドをご参照ください：

• GUI開発ガイド

角度ディスプレイの更新（描画）処理

次は、角度を図示するディスプレイの更新（描画）処理です。これも先ほどの main 関数から呼んでいましたし、他にも複数の箇所から（変換実行時などに）呼ばれます。

これは図形的なあれこれを含んでいるので、この記事のボリューム内で簡潔に説明するのはちょっと難しいです。一応「何をやっているか」だけ触れると、まず前提となるのは：

• drawLine 関数： 2点間の線を引く関数
• drawEllipse 関数： 円（や楕円）を描く関数
• drawPoint 関数： 点を描く関数
• round 関数： 値を丸める関数
  （計算した座標をピクセル単位に換算する際の誤差軽減に使用）

で、これらをいわば「お絵描きの道具」として使って、角度を図示する絵を描いています。

その際の図形的な計算のあれこれについては、sin 関数や cos 関数が図形的に何を意味するのかを意識しながら、コメントと処理を地道に掘り返してもらうしかないかもしれません（すみません）。 筆者自身、コードを書いている最中に「あれ？」とか「どっかおかしいな？」とか思いつつ直しつつを繰り返して書いているので…

なお、上記の関数などを用いた、描画処理の流れなどについては、下記ガイドをご参照ください：

• 2D開発ガイド

ボタンが押された際のイベント処理

ここからは後半、イベント処理です。具体的には、ユーザーがGUIを操作した際などに実行される処理です。まずはボタンが押された際の処理です：

この onButtonClick 関数は、コード内のどこからも呼ばれていませんが、何らかのボタンが押されると自動で実行されます。 これはVCSSLではそう決まっているからです。登録なども要りません。このあたりについては、GUI開発ガイドのイベント処理の回などをご参照ください。

さて、onButtonClick 関数が実行される際に、最初の引数 componentID に、押されたボタンのIDが渡されます。 今回のコードの場合、ボタンのIDはグローバル変数に控えていて、「 degreeToRadianButton 」が度からラジアンへの変換ボタン（>>）、「 radianToDegreeButton 」がラジアンから度への変換ボタン（<<）です。

なので、引数 componentID に渡されたIDに応じて、if 文でどちらのボタンが押されたか分岐し、それぞれに対応した変換処理を行っています。

それぞれの処理の詳細はコメントの通りですが、ラジアンと度との変換処理は、先ほど main 関数の後で宣言した degreeToRadian 関数や radianToDegree 関数を用いています。

スライダーが操作された際のイベント処理

その次は、スライダーが操作された際に実行される onSliderMode 関数を宣言しています：

今回のコードでは、スライダーは、角度を図示するディスプレイの下に配置して、角度を操作するUIとして使っています。 なので上では、スライダーから値をとってきて、ラジアンと度の値を求めて表示しつつ、角度の図示も更新しています。

ウィンドウが閉じられた際のイベント処理

さて、最後です。ウィンドウが閉じられた際に実行される onWindowClose 関数です：

これは単に、プログラムを exit 関数で終了させているだけです。最後はあっさりですね。

◇

以上です。今回は久しぶりに少し長い説明だったので少し疲れました…

ライセンス

このVCSSL/Vnanoコード（ 拡張子が「.vcssl」や「.vnano」のファイル ）は実質的な著作権フリー（パブリックドメイン) である CC0 の状態で公開しています※。 記事中にC言語/C++/Java言語などでのサンプルコードが掲載されいてる場合は、それらについても同様です。 そのままでのご利用はもちろん、改造や流用などもご自由に行ってください。

※ ただし、このコードの配布フォルダ内には、ダウンロード後すぐに実行できるように、 VCSSLの実行環境も同梱されており、そのライセンス文書は「 License 」フォルダ内に同梱されています （要約すると、商用・非商用問わず自由に使用できますが、使用の結果に対して開発元は一切の責任を負いません、といった具合の内容です）。 配布フォルダ内の各構成物の一覧やライセンスについては「 ReadMe_使用方法_必ずお読みください.txt 」をご参照ください。

※ Vnano の実行環境については、別途スクリプトエンジンのソースコードも一般公開しており、 何らかのソフトウェア内に組み込んでご利用いただく事も可能です。詳細はこちらをご参照ください。

この記事中の商標などについて

• OracleとJavaは、Oracle Corporation 及びその子会社、関連会社の米国及びその他の国における登録商標です。文中の社名、商品名等は各社の商標または登録商標である場合があります。
• Windows は、米国 Microsoft Corporation の米国およびその他の国における登録商標です。この記事は独立著作物であり、Microsoft Corporation と関連のある、もしくはスポンサーを受けるものではありません。
• Linux は、Linus Torvalds 氏の米国およびその他の国における商標または登録商標です。
• その他、文中に使用されている商標は、その商標を保持する各社の各国における商標または登録商標です。