» 詳しい使用方法や、エラーで展開できない際の対応方法などはこちら
Vnano版 | 積分値を求めるプログラム (数値積分)
積分の計算を数値的に行い、求まった積分値を表示するプログラムです。 標準では精度重視でシンプソン法という方法を用いていますが、1行だけ書き換えると、 シンプルでわかりやすい矩形法や台形法のコードにもできます。
コードは Vnanoで記述していますが、コード解説の項目において、C言語/C++/Java言語で書いたコードも配布しています。 また、Vnano は VCSSL のサブセットであるため、拡張子を変えればそのままVCSSLのコードとしても動きます(その場合、コード先頭の import 文のコメントアウトは外してください)。
なお、積分された関数のグラフを描きたい場合は 次回の記事 のコードをご使用ください。
使用方法
ダウンロードと展開(解凍)
まず、PC(スマホは未対応)で上の画面の「 ダウンロード 」ボタンを押してください。 するとZIP形式で圧縮されたファイルがダウンロードされます。
その後、ZIPファイルを右クリックして「すべて展開」や「ここに展開」などで展開(解凍)してください。 展開が成功すると、ZIPファイルと同じ名前のフォルダができ、その中にZIPファイルの中身が入っています。
» 展開がエラーで止まってしまう場合や、ファイル名が文字化けしてしまう場合は…
プログラムの起動
Windows をご使用の場合
上記でZIPファイルを展開したフォルダ内にある、以下のバッチファイルをダブルクリック実行してください:
もしプログラムを書き変えながら使いたい場合は、代わりに「 VCSSL_Editor__プログラム編集はこちら.bat 」を実行してください。
正常に起動できると、初回のみ、Java実行環境を入手するか等を尋ねられるので、適時答えて済ませると、プログラムが起動します。 2回目以降はすぐに起動します。
Linux 等をご使用の場合
ZIPファイルを展開したフォルダ内へコマンドライン端末で cd して、以下の通り入力して実行してください:
(プログラムの内容を書き変えながら使いたい場合は、代わりに VCSSL_Editor.jar を実行)
» javaコマンドが使用できない等のエラーが表示される場合は…
起動後
積分値の表示
起動すると、まず黒いウィンドウ(VCSSLコンソール)が表示されて計算処理が始まり、 完了すると小さなウィンドウが立ち上がり、そこに積分値が表示されます。
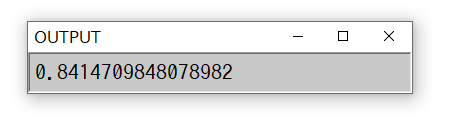
標準では、計算はすぐに終わりますが、スクリプト内の N の値を大きくすると、計算完了までに時間がかかるようになります。
被積分関数(積分対象の関数)や積分区間などの変更
積分内容を変更するには、スクリプト「 IntegralOutput.vnano 」内で宣言されている、 関数 f(x) の内容や変数 A, B の値、および数値積分の区間分割数 N(コード解説 の項目参照)の値を書き変えてください。 標準では cos(x) を x = 0 から 1 までの区間で積分するようになっています。
// =======================================================================
// 以下、積分内容の設定
// =======================================================================
// 被積分関数 (積分対象の関数)
double f(double x) {
return cos(x);
}
double A = 0.0; // 積分区間の下端 (x軸上の左端)
double B = 1.0; // 積分区間の上端 (y軸上の左端)
int N = 10000; // 数値積分における区間分割数 (刻み数)
計算アルゴリズムの切り替え
アルゴリズムは、矩形法、台形法、シンプソン法を使用できます。 スクリプト内で、それぞれのアルゴリズムによる計算行が書かれています(意味は コード解説 の項目参照)。 それらの行の先頭に、行を読み飛ばす記号「 // 」を付け外しして、使うアルゴリズムを選択してください。 標準ではシンプソン法が使用されます。
// -------------------------------------------------------------------
// 以下、i 番目の微小区間の面積を求め、積分値に加算 (どれか 1 つ選択)
// -------------------------------------------------------------------
// 矩形法 (長方形で近似した微小領域の面積を足す)
// value += f(x) * delta;
// 台形法 (台形で近似した微小領域の面積を足す)
// value += ( f(x) + f(x+delta) ) * delta / 2.0;
// シンプソン法 (二次関数で近似した微小領域の面積を足す)
value += ( f(x) + f(x+delta) + 4.0 * f(x+delta/2.0) ) * delta / 6.0;
その他、積分された関数のグラフ化など
以下の記事で、今回のスクリプトを少し改変し、積分された関数をグラフ化するための内容を出力するようにしたバージョンを配信していますので、そちらへどうぞ (実際にグラフを表示する方法なども解説しています):
コード/アルゴリズムの解説
コード全体
このプログラムのコードはVnanoで記述されています。 VnanoはC言語系のシンプルな文法を持っているので、C系の言語に触れられた事のある方なら、 コメントを参考にしながらコード内容を比較的簡単に追う or 改造する事ができると思います。
まずは、コード全体を見てみましょう:
coding UTF-8; // 文字コード宣言 (文字化け予防)
// import Math; // VCSSLでは必要 (Vnanoでは実行ソフト側で必要に応じて設定)
// =======================================================================
// 以下、積分内容の設定
// =======================================================================
// 被積分関数 (積分対象の関数)
double f(double x) {
return cos(x);
}
double A = 0.0; // 積分区間の下端 (x軸上の左端)
double B = 1.0; // 積分区間の上端 (y軸上の左端)
int N = 10000; // 数値積分における区間分割数 (刻み数)
// =======================================================================
// 以下、積分の値を数値的に求める処理
// =======================================================================
double delta = (B - A) / N; // 足し上げる微小区間の幅 (刻み幅)
double value = 0.0; // この変数に積分値を足し上げていく
// 積分区間をN分割した微小区間を、左(下端)から右(上端)へ順に辿るループ
for(int i=0; i<N; ++i) {
// i 番目の微小区間における、左端の x 座標値を求める
double x = A + i * delta;
// -------------------------------------------------------------------
// 以下、i 番目の微小区間の面積を求め、積分値に加算 (どれか 1 つ選択)
// -------------------------------------------------------------------
// 矩形法 (長方形で近似した微小領域の面積を足す)
// value += f(x) * delta;
// 台形法 (台形で近似した微小領域の面積を足す)
// value += ( f(x) + f(x+delta) ) * delta / 2.0;
// シンプソン法 (二次関数で近似した微小領域の面積を足す)
value += ( f(x) + f(x+delta) + 4.0 * f(x+delta/2.0) ) * delta / 6.0;
}
// 結果を表示
output(value);
なお、上に掲載した今回のコードは、以下の数値積分の連載解説記事における 3 つのコードを、 今回の記事用に 1 つのコードに統合したもの ※ です:
- 第1回: 矩形法(長方形近似)による数値積分
- 第2回: 台形法(台形近似)による数値積分
- 第3回: シンプソン法による数値積分
- 今回(総集編): 積分値を計算するプログラム
という事で、解説も 3 回の要点を、短めにまとめた形でコードを追っていきましょう。総集編のような感じです。
上記の連載では、アルゴリズムを説明した後にコードを見ましたが、 今回は記事を短くまとめるため、コードを読みながら、同時にアルゴリズムも説明していきます。 もし、内容が少し駆け足すぎると感じた方は、代わりに上記の連載記事をご参照ください。それでは、以下でコードの各部を掘り下げて解説していきます。
コード先頭
まずは先頭部分です。 ここは、数値積分の計算処理とは無関係なため、そちらに興味がある場合は読み飛ばしても大丈夫です。 一応ですが、ここで行っている事は以下の通りです:
coding UTF-8; // 文字コード宣言 (文字化け予防)
// import Math; // VCSSLでは必要 (Vnanoでは実行ソフト側で必要に応じて設定)
最初の「 coding 〜 」の行では、文字化け対策で、プログラムのファイルが「UTF-8」という文字コードで書かれている事を表しています。
続く「 import 〜 」の行は、簡単に言うと、このコードで数学関数を使う事を宣言しています(Vnanoでは、アプリ側でライブラリ読み込み設定を行うため、必須ではありません)。
被積分関数(積分対象の関数)や積分区間などの定義
その後に、被積分関数や積分区間、および数値積分用のパラメータを定義している箇所が続きます:
// =======================================================================
// 以下、積分内容の設定
// =======================================================================
// 被積分関数 (積分対象の関数)
double f(double x) {
return cos(x);
}
double A = 0.0; // 積分区間の下端 (x軸上の左端)
double B = 1.0; // 積分区間の上端 (y軸上の左端)
int N = 10000; // 数値積分における区間分割数 (刻み数)
積分内容を変える際は、ここの内容を変更してください。 基本的には上記のコード内コメントの通り、積分したい関数をそのままコード内の f(x) 関数として定義し、 積分区間下端の x 値を変数 A に、上端の x 値を変数 B に設定します。
N については、数値積分における微小区間の分割数(いわゆる "刻み" の数)で、 詳細はこの次の項目参照なのですが、基本的には大きいほど精度が上がる半面、計算時間が増えます。 ただしあまり大きくすると、計算ループ回数が増え、丸め誤差やその他微小誤差の蓄積的な寄与が逆に増大してしまうため、 ほどほどの大きさの範囲で、アルゴリズムを切り替えながら、必要な桁まで信頼できる値が出ていると判断できるあたりに設定します(関数の凹凸の激しさ等によって異なります)。
積分値を計算している部分
その後がいよいよこのスクリプトの中心的な処理である、「 積分の値を数値的に求める 」部分です:
// =======================================================================
// 以下、積分の値を数値的に求める処理
// =======================================================================
double delta = (B - A) / N; // 足し上げる微小区間の幅 (刻み幅)
double value = 0.0; // この変数に積分値を足し上げていく
// 積分区間をN分割した微小区間を、左(下端)から右(上端)へ順に辿るループ
for(int i=0; i<N; ++i) {
// i 番目の微小区間における、左端の x 座標値を求める
double x = A + i * delta;
// -------------------------------------------------------------------
// 以下、i 番目の微小区間の面積を求め、積分値に加算 (どれか 1 つ選択)
// -------------------------------------------------------------------
// 矩形法 (長方形で近似した微小領域の面積を足す)
// value += f(x) * delta;
// 台形法 (台形で近似した微小領域の面積を足す)
// value += ( f(x) + f(x+delta) ) * delta / 2.0;
// シンプソン法 (二次関数で近似した微小領域の面積を足す)
value += ( f(x) + f(x+delta) + 4.0 * f(x+delta/2.0) ) * delta / 6.0;
}
各行の意味はコメントに記載の通りですが、しかし予備知識なしにいきなり上のコメント類を見ても、「 微小区間の左端 ??? 台形で近似 ??? 」といった具合に混乱すると思います。
そこで少し、かけ足な説明で、数値積分の処理のイメージを大まかに抑えておきましょう。
手計算では微分を逆に解いて求めるが…
まず「 積分をどうやって求めるか 」ですが、 手計算の場合は微分を逆算、つまり「 微分すると f(x) になるような関数 」を求める事で解きますよね。 これがまたご存知の通り面倒でややこしくて、それで「 積分なんて可能な限り見たくない 」となった方も多いと思います。
※ 画像は脳内のイメージです。
その方法では、面倒な代わりに、厳密な答え(被積分関数の数式表現)を得られるという、色々な面で(特に理論的な解析などでは)強い利点があります。 一方で実用上は、「 ある下端 a から上端 b までの定積分の値が必要な精度で分かったり、積分された関数のグラフの形が必要な区間で分かれば、それだけで十分 」という事もよくあるでしょう。 また、そもそも厳密な答え(被積分関数の数式表現)を得る事が不可能という場合もあります。
そこで登場するのが数値積分です。 数値積分では、上述のような「 ある下端 a から上端 b までの定積分の値 」を、コンピュータで(手計算のように数式を変形していく計算ではなく)数値的な計算によって求めます。 それができれば、少し工夫するだけで、積分された関数のグラフの形もだいたい分かります(実際に 次回の記事 で、グラフを描くための処理を扱っています)。
面積をコンピュータで計算する事で積分値を求める
数値積分にも色々な手法がありますが、今回のスクリプトで用いている 3 通りの方法では、どれも「 被積分関数 f(x) と x軸との間の面積(下図参照)を計算する 」事によって、積分値を求めます:
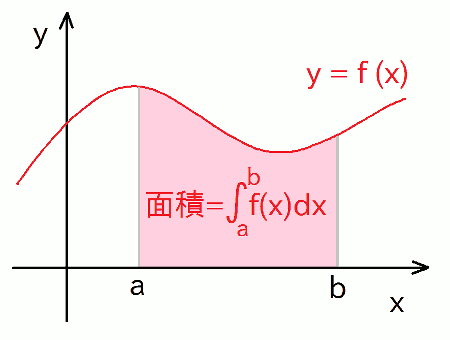
この上図で赤い色で塗った面積が、f(x) の a から b までの定積分の値となります。 これ自体は、積分の定義に関する話として高校数学などでも触れられたかと思いますが、 それがなぜ、どういう条件下(※)で微分の逆として求めた関数(の x=b と x=a での値の差)と一致するかについては、 より厳密な定義や微分/積分可能性などについての意外と難しい議論が必要です。
なので、ここではそういう議論は割愛し、とりあえず積分対象の関数 f(x) は普通の積分可能な関数(値が定まるという意味で、手計算で求まらなくてもよい)で、上の事は前提として使う事にします。
矩形法(長方形近似)
さて、それでは上図で赤く塗った領域の面積を、プログラム的にどうやって求めるのでしょうか?
恐らく一番単純でわかりやすいのは以下のように、 「 領域を N 等分の細かい区間(以下、微小区間と呼びます)に区切って、各区間の面積を、その区間左端での f(x) を高さとする長方形と見なし、それらを全て足し上げる(下図参照) 」 という方法です:
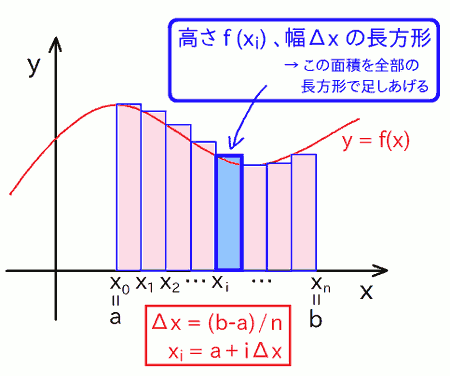
これがいわゆる「 矩形法(長方形近似や長方形公式など、呼び方には結構ローカルなブレがあります) 」です。
イメージが掴めた所で、ここで一旦コード内容に戻りましょう。今回の計算スクリプトで矩形法を使うには、 コード内で「矩形法 〜 」と書かれた行の下の行頭にある「 // 」を外し、代わりにシンプソン法の所には「 // 」を付けて読み飛ばすようにします。 不要な行を削ったシンプルな形で表示すると、以下のようになります:
double delta = (B - A) / N; // 足し上げる微小区間の幅 (刻み幅)
double value = 0.0; // この変数に積分値を足し上げていく
// 積分区間をN分割した微小区間を、左(下端)から右(上端)へ順に辿るループ
for(int i=0; i<N; ++i) {
// i 番目の微小区間における、左端の x 座標値を求める
double x = A + i * delta;
// 矩形法 (長方形で近似した微小領域の面積を足す)
value += f(x) * delta;
}
上の最後にある行の右辺「 f(x) * delta 」が、微小領域に並べた長方形 1 個(幅 delta)の面積で、それを区間下端から上端まで、for 文で x を動かしながら全部足し上げています。
ところで、今の場合は cos(x) を 0 から 1 まで積分しているので、理論上の正しい値は sin 1 = 0.8414709848078965... です。 そこで実際に、矩形法で積分値を計算して、正しい値と比べてみましょう:
分割数 N=10 での結果 0.8637545267950129
分割数 N=100 での結果 0.8437624610086617
分割数 N=1000 での結果 0.8417007635323798
分割数 N=10000 での結果 0.8414939689913762
分割数 N=100000 での結果 0.8414732832893704
この通り、積分区間を微小区間で刻む分割数「 N 」を大きくするほど( = 微小区間の刻み幅を細かくするほど)、結果が正しい値に近づいていっている傾向が見えますね。 この結果から、分割数を 1 桁細かくする、つまり計算量を 10 倍上げると、合っている桁が大体 1 桁増える事が見て取れます。
台形法(台形近似)
続いて「 台形法(こちらも台形近似や台形公式など、呼び方に結構ローカルなブレがあります)」です。 先ほどの矩形法では、微小区間に並べる四角形の上の辺は水平でしたが、それを微小区間の左右での f(x) の値を繋ぐ直線にします(下図参照)。 それによって、四角形の上の辺は傾き、台形になります。なので台形法です。
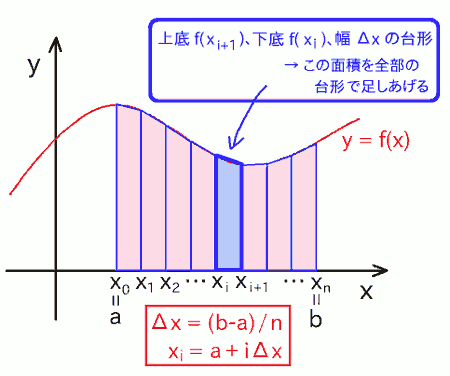
微小区間の刻み幅が同じであれば、先の図からも直感的に、矩形法よりもよく面積を近似できそうですね。 先と同様、今回のスクリプトで台形法を使うようにして、不要な行を削ってシンプルにしたコード内容は:
double delta = (B - A) / N; // 足し上げる微小区間の幅 (刻み幅)
double value = 0.0; // この変数に積分値を足し上げていく
// 積分区間をN分割した微小区間を、左(下端)から右(上端)へ順に辿るループ
for(int i=0; i<N; ++i) {
// i 番目の微小区間における、左端の x 座標値を求める
double x = A + i * delta;
// 台形法 (台形で近似した微小領域の面積を足す)
value += ( f(x) + f(x+delta) ) * delta / 2.0;
}
上の最後にある行の右辺「 ( f(x) + f(x+delta) ) * delta / 2.0 」が、微小領域に並べた台形 1 個(幅 delta)の面積で、それを区間下端から上端まで、for 文で x を動かしながら全部足し上げています。
実際に計算してみると:
分割数 N=10 での結果 0.8407696420884198
分割数 N=100 での結果 0.8414639725380026
分割数 N=1000 での結果 0.8414709146853138
分割数 N=10000 での結果 0.841470984106668
分割数 N=100000 での結果 0.8414709848008824
この通り、分割数を 1 桁細かくする、つまり計算量を 10 倍上げると、合っている桁が大体 2 桁くらいずつ増えている事が見て取れます。 矩形法では2桁増やすには100倍の計算量が要りましたが、台形法では10倍で済んだわけです。お得ですね。
シンプソン法(合成シンプソン法)
最後に、シンプソン法(やシンプソンの公式、名前については後述)です。矩形法 → 台形法と同じ流れで、もっと精度の効率を上げる事を狙います。 まずは先の台形法における、微小領域 1 個を拡大して見てみましょう:
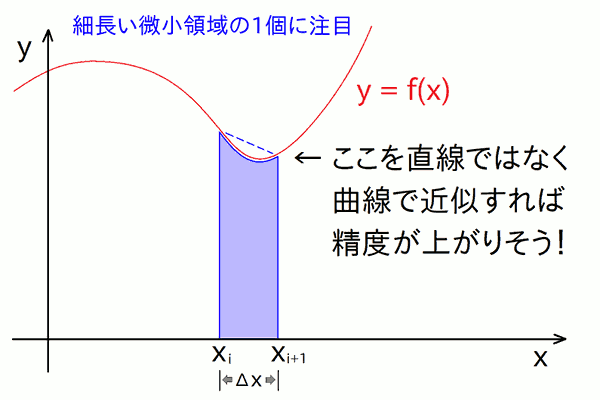
図中に書いてある通りなんですが、微小領域の上の辺が直線だったのを、 関数 f(x) にうまいことフィットする(かつ面積計算が簡単な)曲線にできれば、 より本来の面積( = f(x) と x 軸に囲まれた領域の面積)に近い値が得られそうです。
という事で、微小区間の上の辺を、「 微小区間の両端と真ん中 ※ において、f(x) と同じ点を通る二次関数 」で近似します。
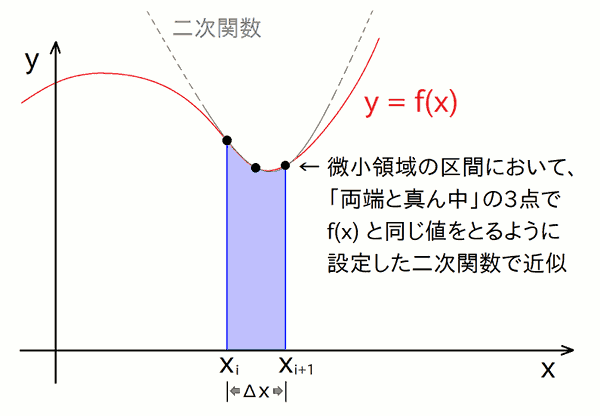
※ ここで、「 両端と真ん中の f(x) を通る二次関数 」という代わりに、 「 隣接する 2 つの微小区間に注目して、その両端と間(両者の境界)の3点の f(x) を通る二次関数 」として解説される事もあります。 というよりも、恐らくそちらの方が教科書的には王道です。
後者は、2 本の微小区間をまとめて 1 本と見なせば、その「 2本の間の値 」は「 1本の真ん中の値 」になるので、本質的には同じ処理です。 ただし、N の定義は2倍ずれるため、両者で実装されたプログラムを比べる場合は、片方のNを2倍して比べないと同じ値は出ません。 また、2つの微小区間に注目するやり方では、N はちゃんと2個ごとに分けても余らないように偶数で(定義によります)選ばないといけない制約が加わる事にも注意が必要です。
そのような制約を忘れると危ない(C言語などで配列の領域外の値を読んだり)のと、本質的には同じ処理をするのにプログラムが逆に複雑になってしまう(2個飛ばしでループしたり)懸念から、 実用上の観点を優先して、筆者は「 真ん中の f(x) を使う 」と見なす実装方法を好んで使っています。 よって、ここでもそう説明しています。ただ、上述の背景などにはご留意ください。やや我流な説明方法かもしれません。
一般に n 次関数は n + 1 個の地点での値が与えられれば 1 通りに定まるので、上図のような二次関数は(微小区間ごとに)1 通りに定まります。 そうすると、二次関数の積分は手で解けるので、(二次関数近似した)微小区間 1 個の面積は、手計算で厳密に求められるはずです。
ここまでの説明で、何かすごく面倒くさそうな計算(高校数学で「 3点を通る二次関数を求めよ 」といった問題に出会った方も多いかも知れません)や、係数を求めるフィッティング処理の実装が要りそうな予感がしたかもしれません。 ところが、その結果は意外とシンプルな形で「 (狭義の)シンプソンの公式 」として公式化されていて、これを用いて:
\[ 微小領域_{i}の面積(近似) = \frac{ f(x_i) + f(x_i + \Delta x) + 4f(x_i+ \Delta x / 2) }{6} \Delta x \]
と求まります。あとは台形法と同様、これを足し上げます。不要な行を削ってシンプルにしたコード内容は:
double delta = (B - A) / N; // 足し上げる微小区間の幅 (刻み幅)
double value = 0.0; // この変数に積分値を足し上げていく
// 積分区間をN分割した微小区間を、左(下端)から右(上端)へ順に辿るループ
for(int i=0; i<N; ++i) {
// i 番目の微小区間における、左端の x 座標値を求める
double x = A + i * delta;
// シンプソン法 (二次関数で近似した微小領域の面積を足す)
value += ( f(x) + f(x+delta) + 4.0 * f(x+delta/2.0) ) * delta / 6.0;
}
となります。 上の最後にある行の右辺「 ( f(x) + f(x+delta) + 4.0 * f(x+delta/2.0) ) * delta / 6.0 」が、先に挙げた数式をそのままコードにしたもので、微小領域 1 個(幅 delta)の面積です。 それを、区間下端から上端まで、for 文で x を動かしながら全部足し上げています。
以上がシンプソン法の処理の流れですが、呼称については狭義の(微小区間 1 個に対して使った)シンプソン公式との呼び分けがややこしく、 かと言って合成シンプソン法/公式と呼ぶのも後述のように微妙なややこしさがあるので、 曖昧さを排除したい場面では、多少まわりくどくてもストレートに「 シンプソン公式で微小区間の面積を1個1個求めて逐次的に足し上げている 」 と言った方が確実に伝わって無難だと思います(下記参照)。
筆者の馴染みのある範囲では、コードを実装する文脈において日本語で「 シンプソン法/公式で数値積分する 」というと、 (狭義の)シンプソン公式を一回使うだけではなく、上のように、細かく刻んだ微小区間に対するシンプソン公式の値の和を計算する場合が多いと思います。 今回のスクリプトでも、それをひっくるめてシンプソン法と呼んでいます。 一方、シンプソンの公式もシンプソン法も、元々の英語に直すと「 Simpson's rule 」で、少しややこしいです(和訳としてはさらにシンプソン則なども加わります)。
そこで、微小区間で刻んで足し上げた値を表す公式として、「合成シンプソン公式」というものがあります。 こちらは、今回のコードの処理と、理論上は同じ事をやっていて、従って理論上の計算値も等価です。 ただ、こちらは微小領域の和を取る Σ の項を少し整理した形の式を指すのが主なようです。 理論上は等価な式でも、式の整理の度合いが異なると、実際のプログラム処理では完全に同一とはならず、計算値の末尾の数桁に出る誤差(なのでそもそも正しい値ではない)の出方が異なったりします。 例えば Σ を求めるループの回し方や足す内容が異なると、丸め誤差の乗り方や乗る順序が変わってくるからです。 なので、完全に同じ値を出さないといけない場面(例えば複数人で同じ処理を独立に書いてみて、互いの値を比べる事で、何か深い勘違いによる実装ミスを洗い出すなど)で「 合成シンプソン公式で計算した 」と言うのは混乱を招く可能性があると思います。
なお、1点の積分値を求めるだけなら、Σ の項を整理した形の合成シンプソン公式の値を、直接求めても構いません(それならはっきりと「合成シンプソン公式で計算した」と言えます)。 しかしながら、次回の記事 で行うように、積分された関数の形を得る(グラフを描く)ためには、そのように整理せず、 今回のように区間毎の値を単純に積算していく必要があります。他にも何かと便利なため、ここではそうしています。
さて、実際の計算結果は:
分割数 N=10 での結果 0.8417720922382719
分割数 N=100 での結果 0.8414710140343371
分割数 N=1000 での結果 0.8414709848108186
分割数 N=10000 での結果 0.8414709848078956 (数値の精度限界付近)
分割数 N=100000 での結果 0.8414709848078982 (数値の精度限界付近)
この通り、分割数を 1 桁細かくする、つまり計算量を 10 倍上げると、合っている桁が大体 4 桁くらいずつ増えている事が見て取れます。 矩形法では4桁増やすには1万倍の計算量が要りましたし、台形法でも100倍要りましたが、シンプソン法では10倍で済んだわけです。かなりお得ですね。
なお、上にも表れていますが、計算処理に用いている数値(この場合は 64-bit の浮動小数点数)の精度限界を超えて、合っている桁数を伸ばす事はできません。 なので、その事を忘れてあまりやたらと細かく刻み過ぎると、逆に演算回数が増える事による誤差蓄積が効いてきて、合っている桁数が減ってしまうという、 精度的にもったいない事になってしまう可能性があります。 最適な N の領域は、積分対象の f(x) の凹凸の激しさ等によって異なります。その判断の際に、上で見てきたような収束具合や、他アルゴリズムとの比較などが参考になります。
最後に
今回の内容は以上です。 この種のテーマの個人的な面白ポイントは、コード上の僅かな違いで精度が劇的に違ってくる事なので、 もしそのあたりの面白さを少しでも感じていただけたなら、とても嬉しく思います。
次回は、今回のコードを少しだけ書き変えて、積分された関数のグラフを描いてみましょう!
ライセンス
このVCSSL/Vnanoコード( 拡張子が「.vcssl」や「.vnano」のファイル )は実質的な著作権フリー(パブリックドメイン) である CC0 の状態で公開しています※。 記事中にC言語/C++/Java言語などでのサンプルコードが掲載されいてる場合は、それらについても同様です。 そのままでのご利用はもちろん、改造や流用などもご自由に行ってください。
※ ただし、このコードの配布フォルダ内には、ダウンロード後すぐに実行できるように、 VCSSLの実行環境も同梱されており、そのライセンス文書は「 License 」フォルダ内に同梱されています (要約すると、商用・非商用問わず自由に使用できますが、使用の結果に対して開発元は一切の責任を負いません、といった具合の内容です)。 配布フォルダ内の各構成物の一覧やライセンスについては「 ReadMe_使用方法_必ずお読みください.txt 」をご参照ください。
※ Vnano の実行環境については、別途スクリプトエンジンのソースコードも一般公開しており、 何らかのソフトウェア内に組み込んでご利用いただく事も可能です。詳細はこちらをご参照ください。
この記事中の商標などについて
- OracleとJavaは、Oracle Corporation 及びその子会社、関連会社の米国及びその他の国における登録商標です。文中の社名、商品名等は各社の商標または登録商標である場合があります。
- Windows は、米国 Microsoft Corporation の米国およびその他の国における登録商標です。この記事は独立著作物であり、Microsoft Corporation と関連のある、もしくはスポンサーを受けるものではありません。
- Linux は、Linus Torvalds 氏の米国およびその他の国における商標または登録商標です。
- その他、文中に使用されている商標は、その商標を保持する各社の各国における商標または登録商標です。
|
角度の「度」とラジアンとを相互変換し、図示もするツール |
|
|
|
45度などの「度」の値と、ラジアンの値とを相互に変換できるツールです。対応する角度の図示もできます。 |
|
FizzBuzz の答えを表示するプログラム |
|
|
|
プログラミングの練習問題としても有名な、FizzBuzz 問題の答えを表示するプログラムの例です。 |
|
Vnano版 | 積分値のグラフ描画用データを出力するプログラム |
|
|
|
数値的に積分を行い、結果の関数をグラフに描くためのデータを出力するコードです。 |
|
Vnano版 | 積分値を求めるプログラム (数値積分) |
|
|
|
矩形法/台形法/シンプソン法を用いて、積分の値を数値的に求めるコードです。 |
|
入力された数式を積分して値とグラフを表示するツール |
|
|
|
画面上で数式を入力すると、それを数値的に積分し、値とグラフを表示してくれるGUIツールです。 |
|
シンプソン法による数値積分 |
|
|
|
積分の値を数値的に求めます。台形法よりも高精度な方法として、被積分関数を微小区間内で二次関数近似して求めた面積を足しあげる、シンプソン法を使用します。 |
|
台形法(台形近似)による数値積分 |
|
|
|
積分の値を数値的に求めます。長方形近似よりも高精度な方法として、台形で近似した微小領域を足しあげる方法を使用します。 |
|
矩形法(長方形近似)による数値積分 |
|
|
|
積分の値を数値的に求めます。長方形の短冊(矩形)で近似した微小領域を足しあげる、最も単純な方法を使用します。 |
|
小数(浮動小数点数)から分数へ近似的に変換するツール |
|
|
|
小数(浮動小数点数)を、適当な誤差の範囲内で、近い分数に変換してくれるツールプログラムです。 |
|
円周率1万桁の計算(ガウス=ルジャンドル法) |
|
|
|
ガウス=ルジャンドル法により、円周率を1万桁まで計算するプログラムです。 |
|
試し割り法による素数判定ツール |
|
|
|
試し割り法を用いて、素数判定を行ってくれる簡易ツールです。 |