台形法（台形近似）による数値積分

このVCSSLプログラムでは、 前回に引き続き、積分の値を数値的に求めます。 アルゴリズムとしては、前回からもう少し進歩して、 台形の微小領域の面積を足しあげる方法を使用します。 コード上ではたった一行の改良でしかないのですが、それで計算精度が劇的に向上するのがポイントです。

なお、今回のプログラムは、あくまでアルゴリズム解説のためのサンプルコード的なものなので、 リッチなGUIの入力画面などはありません。 被積分関数やパラメータを変えたい場合などは、コード内の記述を直接書き換えてください （ または、上のおすすめリンクにある、GUI版の積分ツールをご利用ください ）。

コードはVCSSLで記述されていますが、 適当に別の言語などに書き換えて使って頂いても構いません（ C言語版のコード と C++版のコード も下で掲載しています）。 このコードは著作権フリー（パブリックドメイン / CC0）なので、自己責任でご自由にご使用ください。

[ 数値積分シリーズの連載記事 ]

• 第1回： 矩形法（長方形近似）による数値積分（前回）
• 第2回： 台形法（台形近似）による数値積分（今回）
• 第3回： シンプソン法による数値積分（次回）
• 総集編 ： 積分値を求めるプログラム
• 応用 ： 入力された数式を積分して値とグラフを表示するツール

スポンサーリンク

---

使用方法

ダウンロードと展開（解凍）

まず、PC（スマホは未対応）で上の画面の「 ダウンロード 」ボタンを押してください。 するとZIP形式で圧縮されたファイルがダウンロードされます。

その後、ZIPファイルを右クリックして「すべて展開」や「ここに展開」などで展開（解凍）してください。 展開が成功すると、ZIPファイルと同じ名前のフォルダができ、その中にZIPファイルの中身が入っています。

» 展開がエラーで止まってしまう場合や、ファイル名が文字化けしてしまう場合は…

プログラムの起動

Windows をご使用の場合

上記でZIPファイルを展開したフォルダ内にある、以下のバッチファイルをダブルクリック実行してください：

もしプログラムを書き変えながら使いたい場合は、代わりに「 VCSSL_Editor__プログラム編集はこちら.bat 」を実行してください。

正常に起動できると、初回のみ、Java実行環境を入手するか等を尋ねられるので、適時答えて済ませると、プログラムが起動します。 2回目以降はすぐに起動します。

» うまく起動できずにエラーになってしまう場合は…

Linux 等をご使用の場合

ZIPファイルを展開したフォルダ内へコマンドライン端末で cd して、以下の通り入力して実行してください：

» javaコマンドが使用できない等のエラーが表示される場合は…

起動後

起動すると数値積分の処理が実行され、積分された関数のグラフが表示されます。また、コンソールに積分値も表示されます。

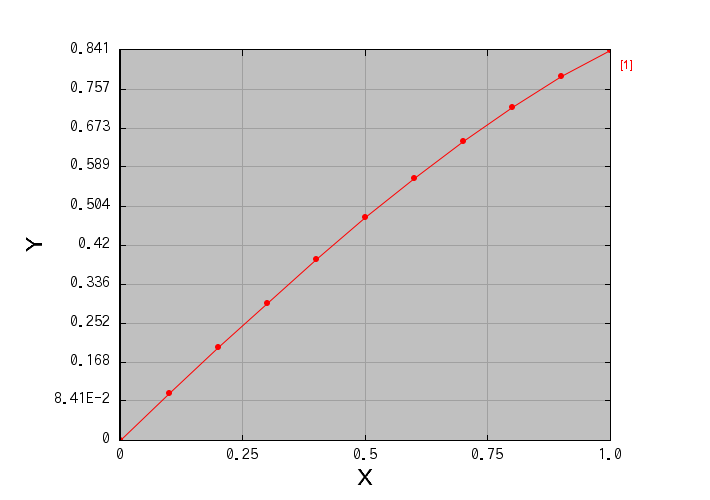
被積分関数やパラメータの変更など

被積分関数や積分区間、精度などを変えたい場合は、 プログラム「 IntegralTrapezoidal.vcssl 」をテキストエディタで開いて、 コードを適当に書き換えてください。

題材解説

前回のおさらい

今回は、前回の記事の発展的な内容となります。そこで、前回の内容を軽くおさらいしてみましょう。 なお、土台をしっかりと固めたいという方は、先に前回の記事をご参照ください。

• 前回： 矩形法（長方形近似）による数値積分

前回は、積分の値を数値的に求める方法として、 X軸と \( y = f(x) \) との間に囲まれた面積を、長方形で細かく区切って求めました。 イメージとしては下図の通りになります。

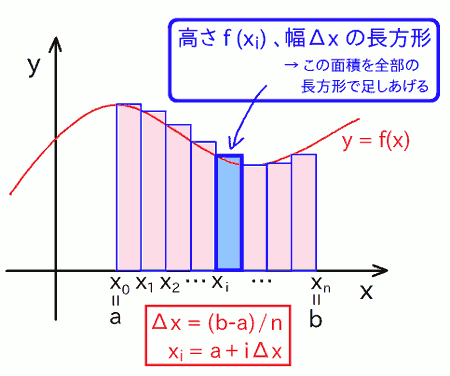
このようにX軸と \( y = f(x) \) との間に囲まれた面積が、 理論上は関数 \( f(x) \) の積分値と等しいのでしたね。

なので、積分の数式を手で解かなくても、プログラムで数値的にこの面積を求めてやれば、積分の値が求まるわけです。 でも、そうすると、どうしても「 誤差 」が生じます。 これは上図からも明らかで、本来は曲面である領域を、長方形を並べたもので強引に近似しているわけですから、はみ出ていたり欠けていたりする箇所が生じています。 これが誤差の元になるわけです。

誤差をどうやって軽減するか ?
―― 長方形から台形に

さて、ここからは今回の内容です。

上で挙げた図を見ながら、 誤差を手っ取り早く軽減するにはどうすればよいか ? と考えると、 まず長方形をもっと細かく刻んでやる事を思いつきます。 これを実際にやってみると、確かに長方形の刻み幅の小ささに正比例して、 誤差が減っていく事が分かります（前回の記事参照）。 しかし、ある程度以上に刻み幅を細かくしても、計算回数が増えすぎて別の誤差が蓄積してしまい、 限界があります。計算時間もかかります。

そういうわけで、同じ刻み幅でも、 もっと誤差を小さくできないか ? という話が重要になるわけです。 そこで今回は、X軸と \( y = f(x) \) との間に囲まれた面積を、 長方形ではなく台形で区切って近似してみましょう（下図）。

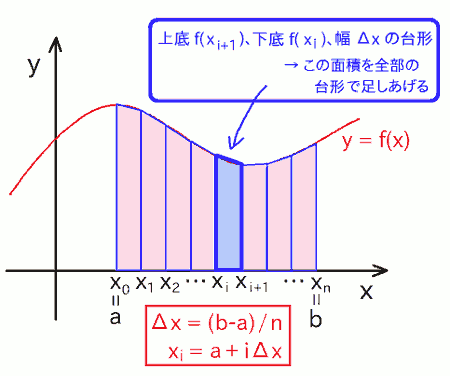
この図を、先に挙げた長方形で刻んだ図と比べてみると、 はみ出たり欠けたりしている部分が少なく、ぱっと見でも明らかに誤差が小さそうですね。 実際、結果を先に言ってしまうと、この「台形法（台形近似）」 は、前回の矩形法（長方形近似）よりも劇的に誤差を軽減できます。

さて、具体的に面積を求める計算についてですが、 まず前回同様に積分区間 a から b までを n 本の台形で刻み、 台形の幅を Δx 、そして i 番目の台形の左下のX値を xi としましょう。つまり：
\[ \Delta x = (b - a) / n \] \[ x_i = a + i \Delta x \]
台形の面積は「（ 下底 + 上底 ）× 高さ(＝幅) ÷ 2 」なので、 i 番目の台形の面積は：
\[ i 番目の台形の面積 = \frac{ ( f(x_i) + f(x_{i+1}) ) }{ 2 } \Delta x \] \[ = \frac{ ( f(x_i) + f(x_i + \Delta x) ) }{ 2 } \Delta x \]
となります。あとはこれを、全ての台形について足しあげれば、領域全体の面積が求まります：
\[ 領域全体の面積（=積分値）= \sum_{i=0}^{n-1} \frac{ ( f(x_i) + f(x_i + \Delta x) ) }{ 2 } \Delta x \]
前回からほんの少し変わっただけですね。実際、プログラムに加える変更もわずかで済みます。

---

スポンサーリンク

---

コード解説

それでは、実際にプログラミングで、台形法（台形近似）により数値積分するコードを見ていきましょう。 このプログラムのコードはVCSSLで記述されています。 VCSSLのコードは大体C言語っぽい感覚で読めると思います。

また、今回は C言語で記述したコード と C++で記述したコード も一緒に掲載します（※）。

コード全体

それでは、コード全体を見てみます。まずは、VCSSLで記述したコードです。50行に満たない程度の短いコードです。

以上です。流れとしては、先頭あたりで被積分関数やパラメータ変数を設定し、 真ん中あたりで for 文のループを回して数値積分の計算を行い、 最後に積分の過程をグラフにプロットするという具合です。

なお、C言語で記述したコードは以下の通りです。

C++で記述したコードは以下の通りです。

以上です。それでは、もう少し具体的に見てみましょう。

前回との違いは 1 行だけ !

コード各部の細かい解説については、前回とほとんど同じなので、 前回のコード解説をご参照ください。 前回のコードと違っている部分は、実は以下の一か所だけです。

[ ↓ 前回のコード ]

[ ↓ 今回のコード ]

これはつまるところ、 長方形の面積を求めていた箇所を、先ほどの台形の面積を求める式：
\[ i 番目の台形の面積 = \frac{ ( f(x_i) + f(x_{i+1}) ) }{ 2 } \Delta x \] \[ = \frac{ ( f(x_i) + f(x_i + \Delta x) ) }{ 2 } \Delta x \]
に変更しただけですね。

さて誤差は ?

この、たった1行だけの変更で、本当に誤差を劇的に減らせるのでしょうか? 実際に実行してみましょう。このプログラムを実行すると、まず積分過程がグラフで表示されます： 今は被積分関数を \( f(x) = \cos x \) と置いているので、 このグラフはそれを積分した \( \sin x \) の形をしているはずです。

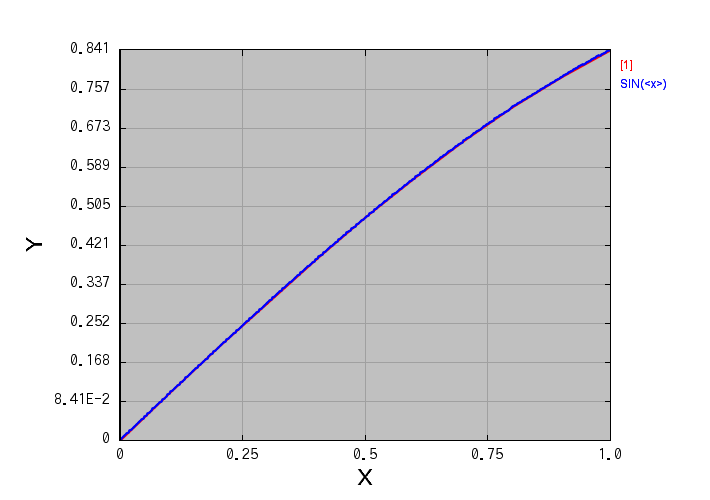
上の図で、赤色の線（重なっていて見づらいですが…）が、今回の計算結果です。 青色の線は、厳密な値と比べるために、\( \sin x \) のグラフを重ね描きしたものです。 ほとんど重なっていますね。今は刻み幅 N = 10、つまりたった10個の台形で面積を近似しているだけなのに、 これだけ厳密な値と一致しているというのは、なかなか良い精度ではないでしょうか。

さて、前回の矩形法（長方形近似）のプログラムで同様に描いたグラフと、 右上の部分（最も厳密値からずれている部分）を比べてみましょう。

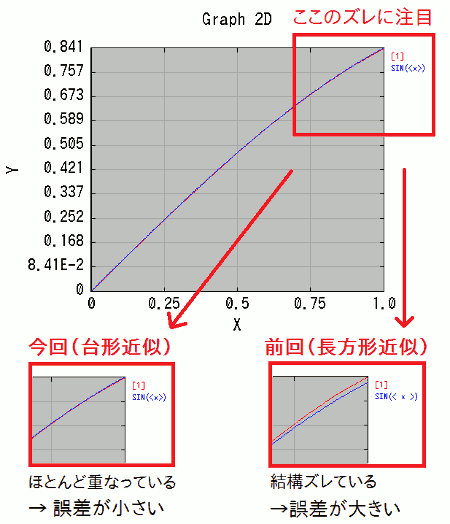
この通り、同じ刻み数 N = 10 で比べても、今回の台形法のほうが、 前回の矩形法（長方形近似）よりも厳密値に近い ＝ 誤差を小さく抑えられている事が分かりますね。 予想通りの結果ではないでしょうか。

刻み幅を細かくしていくと…

誤差が小さく抑えられている事はグラフから大体分かりました。 もう少し厳密に、計算結果の数値から誤差を見てみましょう。 コンソールを見ると、以下のような内容が出力されているはずです：

このように、a から b まで積分していっている最中の x 値が左の列、 その地点までの積分値が右の列に出力されています。 1行ごとに、積分値に台形1個の面積が足されています。 最後の行の積分値 0.8407696420884198 が、最終的に求まった \[ \int^{1}_{0} \cos(x) dx \] の値で、厳密な値は sin 1 なので 0.8414709848... です。小数点以下 3 桁目から食い違っていますね。 この食い違いが誤差です。

さて、台形の刻み幅を細かくするほど、つまり刻み数 N を大きくするほど、誤差は小さく抑えられるはずです。 実際にプログラムにおいて N を増やしていき、先ほどの最終行の値がどうなっていくか見てみましょう：

わかりやすいように、厳密な値（ \(\sin 1\) ）から食い違っている部分を赤色で塗りました。 前回の矩形法（長方形近似）の場合と比べて、やはり誤差が急速に減っていっていますね。

上の結果から、台形法では、刻み数 N を 1 桁上げるごとに、 合っている桁数を大体 2 桁ずつ増やせる事が分かります。 こういうのを一般に「 2次の精度 」と言ったりします。 つまり台形法は 2 次の精度の数値積分アルゴリズムという事になります。

それに対して、前回扱った矩形法（長方形近似）では、刻み数 N を 1 桁上げるごとに、 合っている桁数は大体 1 桁ずつ増えました。 つまり矩形法は 1 次の精度の数値積分アルゴリズムという事になります。

数値積分に限らず、数値計算で使用する色々なアルゴリズムには、このような精度の次数がとても重要です。 一般に、次数が高いほうが、より誤差蓄積を抑えつつ、より高速に計算できるためです。 ただし、あまり次数の高いアルゴリズムは、逆に 1 刻みごとの計算量が増えて計算速度が低下してしまい、 刻み数を増やせなかったりもします。 また、計算の途中過程において、誤差がどのように振る舞うか（単調に増加していくのか、 ある程度の幅で振動するのか）という点も重要です。

今回のような練習ではなく、もっと本格的な数値計算の場においては、そのあたりの事情も総合的に考慮して、 どのアルゴリズムを採用するかを決定します。 個人的に知っている限りでは、 1 次の精度のアルゴリズム（矩形法もそうです）というのは、やはり精度や速度的なデメリットが大きく、 あまり実用されているのは見かけません（※）。

今回の台形法は、覚えやすく簡単でありつつ2次の精度を発揮できるので、そこそこの精度でちょっと積分の値を求めたい、 くらいの場合には実際に結構使えると思います。 なんといっても、あのシンプルな矩形法（長方形近似）から数秒で書き換えられるのに、 精度は一気に跳ね上がるという、 そのコストパフォーマンスの高さはかなか侮れません。 たった一行の違いでこれだけ圧倒的な差が出てくるというのは、 数値計算プログラミングの醍醐味の一つではないでしょうか。

では、台形法を知っていればもう十分かというと… さらにほんの少しだけ書き換えるだけで、なんと 4 次の精度が出るようになります。 という事で、次回は簡単で高速ながらも 4 次の精度を誇る、シンプソン法の数値積分コードを書いてみましょう !

[ 数値積分シリーズの連載記事 ]

• 第1回： 矩形法（長方形近似）による数値積分（前回）
• 第2回： 台形法（台形近似）による数値積分（今回）
• 第3回： シンプソン法による数値積分（次回）

ライセンス

このVCSSL/Vnanoコード（ 拡張子が「.vcssl」や「.vnano」のファイル ）は実質的な著作権フリー（パブリックドメイン) である CC0 の状態で公開しています※。 記事中にC言語/C++/Java言語などでのサンプルコードが掲載されいてる場合は、それらについても同様です。 そのままでのご利用はもちろん、改造や流用などもご自由に行ってください。

※ ただし、このコードの配布フォルダ内には、ダウンロード後すぐに実行できるように、 VCSSLの実行環境も同梱されており、そのライセンス文書は「 License 」フォルダ内に同梱されています （要約すると、商用・非商用問わず自由に使用できますが、使用の結果に対して開発元は一切の責任を負いません、といった具合の内容です）。 配布フォルダ内の各構成物の一覧やライセンスについては「 ReadMe_使用方法_必ずお読みください.txt 」をご参照ください。

※ Vnano の実行環境については、別途スクリプトエンジンのソースコードも一般公開しており、 何らかのソフトウェア内に組み込んでご利用いただく事も可能です。詳細はこちらをご参照ください。

この記事中の商標などについて

• OracleとJavaは、Oracle Corporation 及びその子会社、関連会社の米国及びその他の国における登録商標です。文中の社名、商品名等は各社の商標または登録商標である場合があります。
• Windows は、米国 Microsoft Corporation の米国およびその他の国における登録商標です。この記事は独立著作物であり、Microsoft Corporation と関連のある、もしくはスポンサーを受けるものではありません。
• Linux は、Linus Torvalds 氏の米国およびその他の国における商標または登録商標です。
• その他、文中に使用されている商標は、その商標を保持する各社の各国における商標または登録商標です。