» 詳しい使用方法や、エラーで展開できない際の対応方法などはこちら
シンプソン法による数値積分
このVCSSLプログラムでは、数値積分シリーズの連載の第3回として、前回に引き続き、積分の値を数値的に求めます。 アルゴリズムとしては、前回からもう一歩進歩して、 微小領域の面積をより高い精度で求めて足しあげる、シンプソン法という方法を使用します。 矩形法(長方形近似)や台形法(台形近似)とのコード上での違いは、今回もたったの一行なのですが、 それで計算精度が台形法からさらに劇的に向上するのがポイントです。
なお、今回のプログラムは、あくまでアルゴリズム解説のためのサンプルコード的なものなので、 リッチなGUIの入力画面などはありません。 被積分関数やパラメータを変えたい場合などは、コード内の記述を直接書き換えてください。
コードはVCSSLで記述されていますが、 適当に別の言語などに書き換えて使って頂いても構いません( C言語版のコード と C++版のコード も下で掲載しています)。 このコードは著作権フリー(パブリックドメイン / CC0)なので、自己責任でご自由にご使用ください。
[ 数値積分シリーズの連載記事 ]
- 第1回: 矩形法(長方形近似)による数値積分
- 第2回: 台形法(台形近似)による数値積分(前回)
- 第3回: シンプソン法による数値積分(今回)
- 総集編: 積分値を求めるプログラム(数値積分)
使用方法
ダウンロードと展開(解凍)
まず、PC(スマホは未対応)で上の画面の「 ダウンロード 」ボタンを押してください。 するとZIP形式で圧縮されたファイルがダウンロードされます。
その後、ZIPファイルを右クリックして「すべて展開」や「ここに展開」などで展開(解凍)してください。 展開が成功すると、ZIPファイルと同じ名前のフォルダができ、その中にZIPファイルの中身が入っています。
» 展開がエラーで止まってしまう場合や、ファイル名が文字化けしてしまう場合は…
プログラムの起動
Windows をご使用の場合
上記でZIPファイルを展開したフォルダ内にある、以下のバッチファイルをダブルクリック実行してください:
もしプログラムを書き変えながら使いたい場合は、代わりに「 VCSSL_Editor__プログラム編集はこちら.bat 」を実行してください。
正常に起動できると、初回のみ、Java実行環境を入手するか等を尋ねられるので、適時答えて済ませると、プログラムが起動します。 2回目以降はすぐに起動します。
Linux 等をご使用の場合
ZIPファイルを展開したフォルダ内へコマンドライン端末で cd して、以下の通り入力して実行してください:
(プログラムの内容を書き変えながら使いたい場合は、代わりに VCSSL_Editor.jar を実行)
» javaコマンドが使用できない等のエラーが表示される場合は…
起動後
起動すると数値積分の処理が実行され、積分された関数のグラフが表示されます。また、コンソールに積分値も表示されます。
被積分関数やパラメータの変更など
被積分関数や積分区間、精度などを変えたい場合は、 プログラム「 IntegralSimpson.vcssl 」をテキストエディタで開いて、 コードを適当に書き換えてください。
題材解説
前回までのおさらい
―― 矩形法と台形法
今回は、前回までの記事の発展的な内容となります。そこで、前回までの内容を軽くおさらいしてみましょう。 なお、土台をしっかりと固めたいという方は、先に前回までの記事をご参照ください。
- 第1回: 矩形法(長方形近似)による数値積分
- 第2回: 台形法(台形近似)による数値積分
第1回では、積分の値を数値的に求める方法として、 X軸と \( y = f(x) \) との間に囲まれた面積を、長方形で細かく区切って求めました。 イメージとしては下図の通りになります。
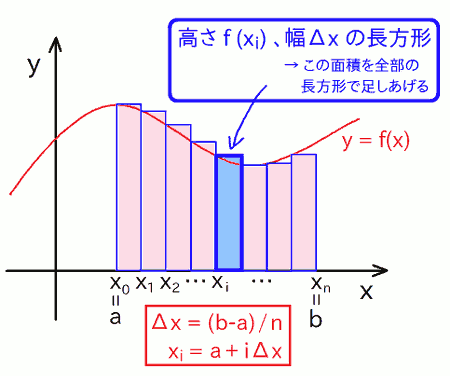
このようにX軸と \( y = f(x) \) との間に囲まれた面積が、 理論上は関数 \( f(x) \) の積分値と等しいのでしたね。 なので、積分の数式を手で解かなくても、プログラムで数値的にこの面積を求めてやれば、積分の値が求まるわけです。
第1回で扱った矩形法(長方形近似)では、実際に上の細長い長方形の面積を足し上げる事で、全体の面積( = 積分値 )を求めました。 でも、そうすると、どうしても「 誤差 」が生じます。 これは上図からも明らかで、領域の上端の線は本来はなめらかな曲線なのに、その領域を長方形を並べたもので強引に近似しているわけですから、 上端がギザギザになって、本来の曲線からはみ出ていたり欠けていたりする箇所が生じています。 これが大きな誤差の元になっていたわけです。
そこで第2回で扱った台形法(台形近似)では、上図の細長い長方形の部分を台形に置き換えて改良する事で、 はみ出たり欠けている部分を減らして、より高精度に全体の面積( = 積分値 )を求めました。このイメージは下図の通りです。
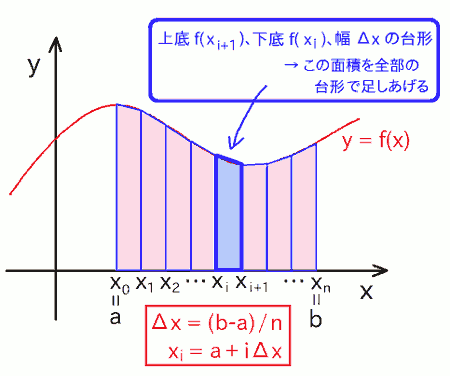
上の図を見ただけでも、矩形法では上端の曲線からガタガタに外れていた部分が、台形法では大分ならされているので、誤差が一気に減りそうな事が直感的にわかります。
実際、細長い微小領域の幅 \( \Delta x \) を小さくしていった際に、矩形法では積分値の誤差がそれに比例して小さくなっていったのに対し、 台形法では \( \Delta x \) の2乗に比例して(より急激に)小さくなっていきました。 具体的には、\( \Delta x \) の幅を10分の1にすると、矩形法では誤差も10分の1に減るのに対して、台形法は誤差が一気に100分の1まで減る、といった具合です。 \( \Delta x \) を100分の1にするなら、矩形法なら誤差も100分の1ですが、台形法なら1万分の1になります。この違いは大きいですね。
ところで、 「 細長い微小領域の幅 \( \Delta x \) を小さくすれば精度が上がるなら、別に台形とか難しい事を考えなくても、 一番シンプルな矩形法で \( \Delta x \) をひたすら細かく刻めばそれでいいんじゃないの?」 という疑問が湧くかもしれません。現在のコンピューターは高速なので、計算時間等がそんなに気にならないなら、ある程度の精度まではその通りです。 しかしコンピューターでの数値計算は、本来は無限桁まで続く小数の値も、有限の桁数で打ち切って扱っているため、 実は四則演算などの基本的な計算を1回行うだけでも、その度に非常に小さな誤差が発生していたりします(データ型にもよります)。 なので、あまり細長い微小領域を細かく刻みすぎると、その面積を足し上げる計算の回数が膨大になってしまって、 逆に上述のような別の誤差が蓄積する事により、ある程度以上は精度を上げられなくなってしまう場合もあります(矩形法で試すと分かりやすいです)。 よって、少ない計算の手数で、より高い精度を出せるなら、それに越した事は無いわけですね。
台形からさらに、誤差をどうやって軽減するか ?
―― 微小領域の上端を曲線で近似
さて、少し長いおさらいでしたが、ここから今回の本題です。 台形法から、もう一歩改良して、精度をさらに向上させてみましょう。
と言っても、大々的に複雑な改修をやるわけではないので、安心してください。最終的に変更するのは、プログラムのコードだと、たったの1行です。 具体的には、細長い微小領域の面積を計算していた部分です。 そう、結局は今回も前回同様、「微小領域の面積をいかに精密に求めるか」という話に尽きるわけですね。 それ以外の部分の考え方や処理の流れは、これまでとぜんぶ同じです。
それではまず、台形法の誤差の原因を見つめ直してみましょう。細長く刻んだ微小領域( = いまは台形で近似 )を1個抜き出して注目します。 わかりやすくするために、f(x) のカーブの曲がり具合は先ほどの図よりも誇張しています。
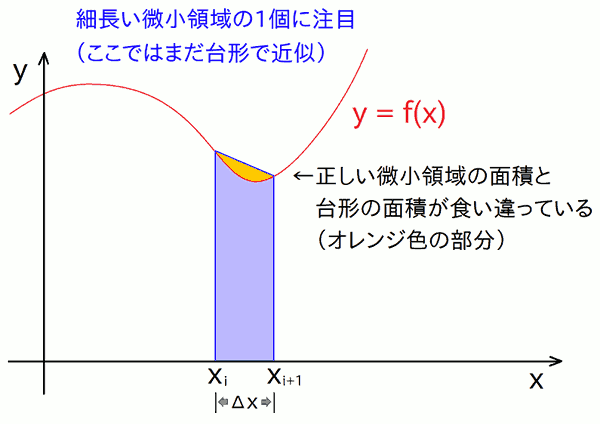
微小領域の上端の線を見ると、矩形法よりはよっぽどマシですが、それでもやはり曲線であるはずの \( f(x) \) を直線で近似しているため、 本来の微小領域の面積と比べて、台形の面積はわずかに食い違っています(図中のオレンジ色の部分)。この食い違っている部分は、\( f(x) \) のカーブ具合に応じて、場所によってはみ出ていたり欠けていたりするでしょう。 この過不足が台形法での誤差の根本原因です。 この微小領域の面積を足して、積分区間全体での面積を求め、それを積分値とするわけですが、その際にこの小さな過不足が積み重なって、最終的に積分値の誤差を生み出しているのです。
では、どうするか? 「 微小領域の上端で、本来は曲線である \( f(x) \) を直線で近似しているから誤差が生じるなら、そこを曲線で近似してやれば精度が上がるのでは? 」 これが、今回の土台となる考え方です。
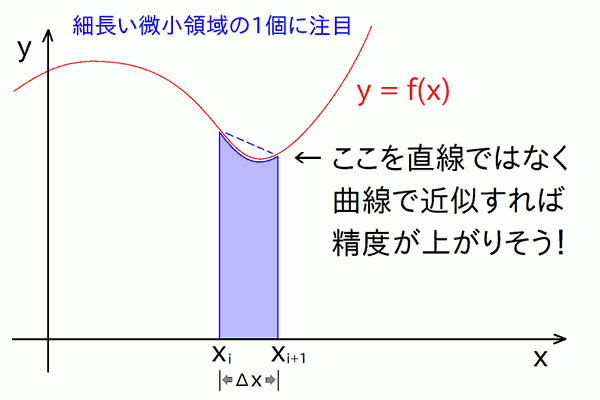
直感的にも、より欠けたりはみ出したりする部分が減り、誤差が減って精度が向上しそうですね。
微小領域の上端をどういう曲線で近似するか?
―― 単純で手でも積分可能な二次関数を使用
ここから先は、微小領域の上端で、\( f(x) \) をどういう曲線で近似するか? という話になるわけですが、ここが今回の肝になるポイントです。
一番誤差が無く完璧なのは \( f(x) \) そのものを使う事ですが、そうすると微小領域の面積を求めるためにまず \( f(x) \) を手計算で積分する必要が出てくるので、意味がなくなってしまいます。 そもそもそれが難しい( or 不可能な )場合のために、プログラムを書いてまでコンピューターに積分をやってもらおうとしているのでしたね。
ならどうするかと言うと、二次関数を使います。二次関数は、下図にも示す通りシンプルな曲線で、そして高校などでも習うように、手でも厳密に積分できますね。 なので、二次関数で \( f(x) \) をいい感じに近似できれば、細長い微小領域の面積は手でも解ける = 式として求まるので、 その式で、台形法で使っていた台形の面積の式を置き替えればいいわけです。
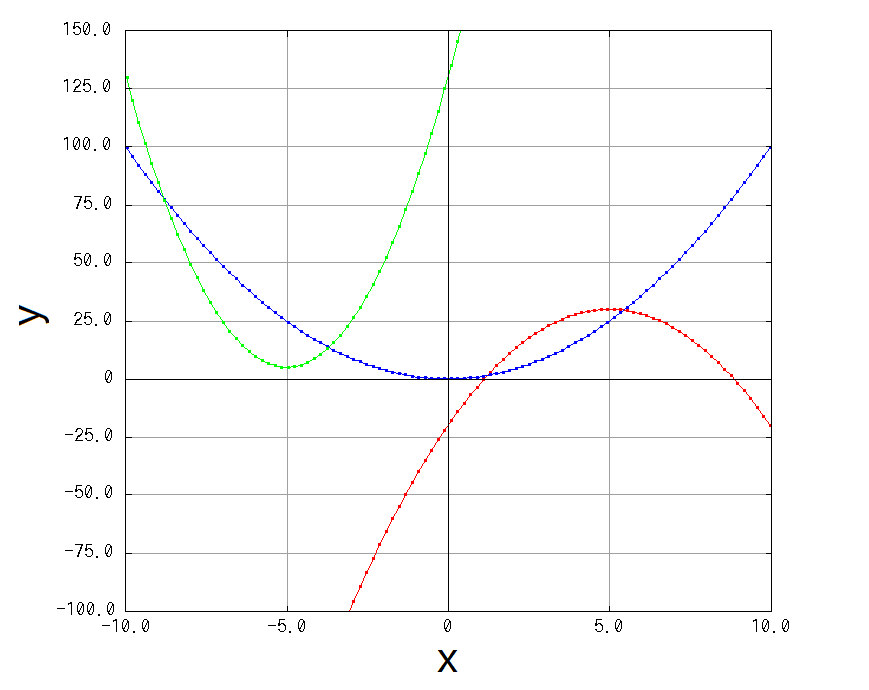
さて、二次関数は中学校でも習う通り、係数などのパラメータによって丸みや位置が変わります(上図参照)。 「 y = 2 x2 + 3 x - 4 のグラフを描け 」みたいなのがテストに出て、四苦八苦しながら位置や丸みを求めて手描きした思い出がある方も、結構多いのではないでしょうか。 ここでは \( f(x) \) の近似が目的なので、微小領域の範囲内で \( f(x) \) のカーブになるべくピタッとフィットするように、こちら側で二次関数の係数を設定してやりましょう。
ここで、「 \( f(x) \) の形は色々な場合があるのに、いわゆる放物線の形をしている二次関数で、毎回都合よく近似できるものなの?
仮に \( f(x) \) が \( \sin x \) とか \( \cos x \) とかだったら、形からして絶対無理じゃないの? 」という疑問が湧くかもしれません。
でも、なにも \( f(x) \) の全体を二次関数で近似しようというわけではないので、大丈夫です。
我々がいま注目しているのは、本当〜に狭い微小領域の中での \( f(x) \) の形です。
\( f(x) \) が普通のなめらかな関数※なら、そんな非常に狭い領域を拡大して眺めると、単に微妙に丸みを帯びたカーブ程度にしか見えないはずです。
そしてそのカーブを多項式で近似する際、対象の領域が狭い(近傍の近似である)ほど、より低い次数の式で、よく近似できるようになるのが普通です。
なので、微小領域を十分に細かく刻むなら、\( f(x) \) を二次関数で近似するのは理にかなっているのです。
( ※ 逆に、どこまで拡大しても複雑な構造があったり、あちこちで不連続だったりする特殊な場合には、うまく近似できません。 )
多項式を関数にフィットさせるための係数の選び方は、一般には色々あります。ただ、あまり計算が複雑になるのも避けたいところです。 そこでここでは結構単純に、細長い微小領域の「両端と真ん中」の3つの地点 ※ において、関数 \( f(x) \) と同じ点を通るように、二次関数の係数を設定します。 両端の2点だけなら、そこを通る二次関数はいくらでも存在しますが、その中には上に膨らんでいたり下に凹んでいたりと様々なものがあるので、 「真ん中の点も通る」というルールを加える事で、\( f(x) \) のカーブ具合にそこそこフィットしてもらおう、というわけですね。
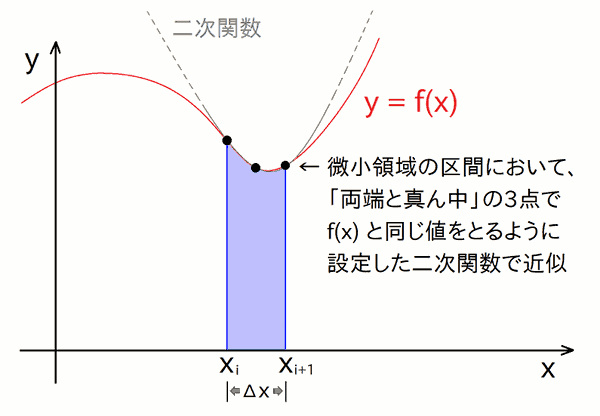
ここで、「 両端と真ん中の f(x) を通る二次関数 」という代わりに、 「 隣接する 2 つの微小区間に注目して、その両端と間(両者の境界)の3点の f(x) を通る二次関数 」として解説される事もあります。 というよりも、恐らくそちらの方が教科書的には王道です。
後者は、2 本の微小区間をまとめて 1 本と見なせば、その「 2本の間の値 」は「 1本の真ん中の値 」になるので、本質的には同じ処理です。 ただし、N の定義は2倍ずれるため、両者で実装されたプログラムを比べる場合は、片方のNを2倍して比べないと同じ値は出ません。 また、2つの微小区間に注目するやり方では、N はちゃんと2個ごとに分けても余らないように偶数で(定義によります)選ばないといけない制約が加わる事にも注意が必要です。
そのような制約を忘れると危ない(C言語などで配列の領域外の値を読んだり)のと、本質的には同じ処理をするのにプログラムが逆に複雑になってしまう(2個飛ばしでループしたり)懸念から、 実用上の観点を優先して、筆者は「 真ん中の f(x) を使う 」と見なす実装方法を好んで使っています。 よって、ここでもそう説明しています。ただ、上述の背景などにはご留意ください。やや我流な説明方法かもしれません。
このように3点を通る二次関数は1通りに絞られて、ここでは割愛しますが、手計算で求められます。
そうすると、あとはその二次関数を積分すれば、細長い微小領域の面積が求まります。
これはシンプソンの公式として知られていて、以下のようにかなり簡単な形で書けます:
\[ i番目の微小領域の面積 = \frac{ f(x_i) + f(x_i + \Delta x) + 4f(x_i+ \Delta x / 2) }{6} \Delta x \]
ここで \( x_i \) は微小領域の左端、\( x_i+\Delta x \) は右端、\( x_i + \Delta x/2 \) は真ん中の x 値であり、\( \Delta x \) は微小領域の幅( \( = x_{i+1} - x_{i} \) )です。
あとはこれを、全ての微小領域について足しあげれば、領域全体の面積が求まります:
\[ 積分値 = \sum_{i=0}^{N-1} \frac{ f(x_i) + f(x_i + \Delta x) + 4f(x_i+ \Delta x / 2) }{6} \Delta x \]
式の上では、もう少し重複部分について整理した形にできますが、コードとの対応では上の形が一番ストレートでわかりやすいので、このままにしておきましょう。 要は、矩形法や台形法で、 足し上げる中身が長方形や台形の面積だったのが、シンプソンの公式を使った二次関数近似の面積に置き換わっただけですね。
コード解説
それでは、実際にプログラミングで、シンプソン法により数値積分するコードを見ていきましょう。 このプログラムのコードはVCSSLで記述されています。 VCSSLのコードは大体C言語っぽい感覚で読めると思います。
また、今回は C言語で記述したコード と C++で記述したコード も一緒に掲載します(※)。
VCSSLのコードでは実行後に自動でグラフプロットまでが行われますが、 C/C++ のコードでは標準出力に積分値が出力されるのみです。 C/C++ の計算結果をグラフ化して見たい場合は、実行時にリダイレクトなどで標準出力内容をファイルに記録し、 適当なグラフソフト(例えば リニアングラフ2D など)でそのファイルを開いて、プロットしてください。
コード全体
それでは、コード全体を見てみます。まずは、VCSSLで記述したコードです。50行に満たない程度の短いコードです。
coding UTF-8; // 文字コードの明示(文字化け予防)
import Math; // 数学関数ライブラリの読み込み
import tool.Graph2D; // グラフ描画ライブラリの読み込み
// 計算条件のパラメータ定数
const double A = 0.0; // 積分区間の下端
const double B = 1.0; // 積分区間の上端
const int N = 10; // 微小区間の刻み数(値を大きく=細かく刻むほど高精度)
// 積分したい関数 f(x) = cos(x)
double f(double x) {
return cos(x);
}
// ---------------------------------------------
// 以下、シンプソン法による数値積分の処理
// ---------------------------------------------
double delta = (B - A) / N; // 微小の幅 Δx
double value = 0.0; // 計算結果の積分値(区間全体の面積)
for(int i=0; i<N; i++) {
// i番目の微小区間の左下X値
double x = A + i * delta;
// i 番目の地点までの積分値をコンソールに出力
println(x, value); // ※ N が大きい時は重いのでコメントアウト
// 積分値に i 番目の微小区間の面積を足す
value += ( f(x) + f(x+delta) + 4.0 * f(x+delta/2.0) ) * delta / 6.0;
}
// 最終的な積分結果(区間全体の面積)をコンソールに出力
println(B, value);
// コンソール内容をグラフにプロット
// ※ N が大きい時は重いのでコメントアウト
setGraph2DData(newGraph2D(), load());
以上です。流れとしては、先頭あたりで被積分関数やパラメータ変数を設定し、 真ん中あたりで for 文のループを回して数値積分の計算を行い、 最後に積分の過程をグラフにプロットするという具合です。
上のコードで double 型を使っていますが、 VCSSL では double 型は float 型と同じものとして扱われ、 現行の処理系では共に倍精度なので、別に float 型を使っても構いません。 今回は、C/C++ のコードと統一するために double 型を用いました。
なお、C言語で記述したコードは以下の通りです。
C++で記述したコードは以下の通りです。
以上です。それでは、もう少し具体的に見てみましょう。
前回との違いは 1 行だけ !
コード各部の細かい解説については、矩形法や台形法からほとんど変わっていないので、 矩形法の数値積分のコード解説をご参照ください。 矩形法や台形法のコードと違っている部分は、以下のたった一か所だけです。
[ ↓ 矩形法のコード ]
...
// 積分値に i 番目の短冊(長方形)の面積を足す
value += f(x) * delta;
...
[ ↓ 台形法のコード ]
...
// 積分値に i 番目の台形の面積を足す
value += ( f(x) + f(x+delta) ) * delta / 2.0;
...
[ ↓ 今回(シンプソン法)のコード ]
...
// 積分値に i 番目の微小区間の面積を足す
value += ( f(x) + f(x+delta) + 4.0 * f(x+delta/2.0) ) * delta / 6.0;
...
これはつまるところ、
長方形や台形の面積を求めていた箇所を、先ほど説明した、シンプソンの公式を使って二次関数近似で面積を求める式:
\[ i番目の微小領域の面積 = \frac{ f(x_i) + f(x_i + \Delta x) + 4f(x_i+ \Delta x / 2) }{6} \Delta x \]
に変更しただけですね。
さて誤差は ?
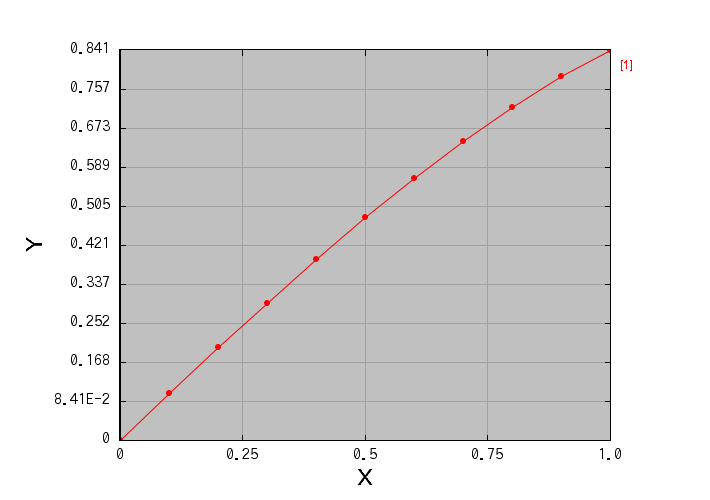
それでは、このたった1行だけの変更で、どれだけ誤差が減るのか見てみましょう。 このプログラムを実行すると、まず積分過程がグラフで表示されます。 今は被積分関数を \( f(x) = \cos x \) と置いているので、 このグラフはそれを積分した \( \sin x \) の形をしているはずです。
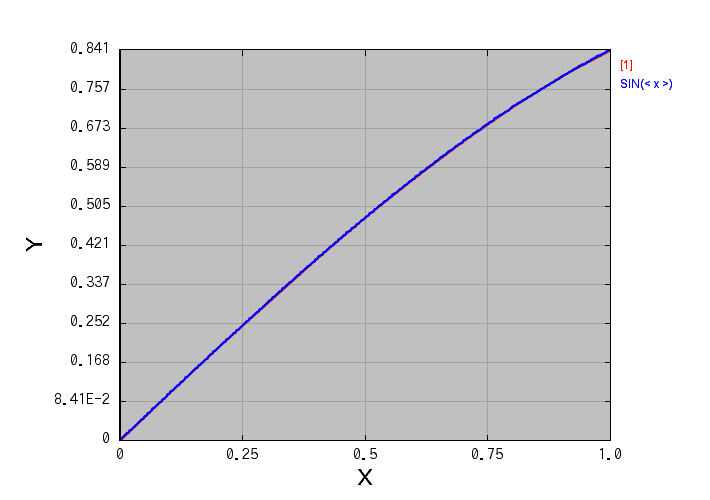
上の図で、赤色の線(重なっていて見づらいですが…)が、今回の計算結果です。 青色の線は、厳密な値と比べるために、\( \sin x \) のグラフを重ね描きしたものです。 前回扱った台形法の時点でも既に両者はかなり重なっていましたが、今回もほぼ重なってしまって区別できません※。 この結果は刻み幅 N = 10、つまり微小区間をかなり粗く刻んでいるのにもかかわらず、です。
現在のVCSSL処理系で採用している2Dグラフソフトは「 リニアングラフ2D 」で、 データに数式を重ねてプロットする機能が付いています。上では、その機能を使いました。 まず、グラフ画面のメニューバーから 「 ツール 」 > 「 数式プロット 」と選択します。 続いて表示されるウィンドウの「 f(<x>)」の入力欄に「 sin(<x>) 」と入力し、 「 PLOT 」ボタンを押します。 すると、グラフの上に、青い線で \( \sin x \) が重ね描きされます。
グラフをものすご〜く拡大すれば一応は厳密値とのズレが見られますが、この水準になると、もう数値で直接ズレを見た方がわかりやすいでしょう。 という事でコンソールを見ると、以下のような内容が出力されているはずです:
0.1 0.09983342011429819
0.2 0.19866933769535547
…
0.8 0.7173561158151355
0.9 0.7833269368344314
1.0 0.8414710140343371
このように、a から b まで積分していっている最中の x 値が左の列、 その地点までの積分値が右の列に出力されています(上で示したグラフでは、このデータを読ませてプロットしています)。 1行ごとに、積分値に微小領域1個の面積が足されています。
最後の行の積分値 0.8414710140343371 が、最終的に求まった \[ \int^{1}_{0} \cos(x) dx \] の値で、厳密な値は sin 1 なので 0.84147098480789650... です。小数点以下 6 桁目から食い違っていますね。 この食い違いが誤差です。
前回扱った台形法では、同じ刻み数 N=10 の条件下で、小数点以下 3 桁目から違っていました。 という事は、シンプソン法で精度が一気に上がった事がわかりますね。 ちなみに、矩形法では小数点以下 2 桁目から違っていました。
さて、微小区間の刻み幅 \( \Delta x \) を細かくするほど、つまり刻み数 N を大きくするほど※、誤差は小さく抑えられるはずです (※ 詳細は矩形法参照ですが、aを積分区間の下端、bを積分区間の上端として、それをN個の微小区間に刻むため、\( \Delta x = (b-a)/N \) です )。
実際にプログラムにおいて N を増やしていき、先ほどの最終行の値がどうなっていくか見てみましょう:
N=10の場合の結果 0.8414710140343371
N=100の場合の結果 0.8414709848108186
N=1000の場合の結果 0.8414709848078956
N=10000の場合の結果 0.8414709848078982
わかりやすいように、厳密な値( \(\sin 1\) )から食い違っている部分を赤色で塗りました。
N = 1 から 1000 までの結果に注目してみると、刻み数Nを1桁増やすごとに、合っている桁数がおおまかに4桁くらいずつ増えている事がわかります(※ラスト2桁の誤差については後述)。 この結果から、シンプソン法は「 4次精度 」の数値積分アルゴリズムである事がわかります。
ところで、前回扱った台形法は2次精度で、Nを1桁増やすごとに、合っている桁数が大体2桁くらいずつ増えるのでしたね。 また、最初に扱った矩形法は1次精度だったので、1桁ずつしか増えませんでした。 一方で、4次精度を誇るシンプソン法を使えば、Nをちょっと増やすだけで一気に「4段飛ばし」で精度が増えていくわけです。 これらの数値積分法のプログラムのコードは、それぞれたった1行違うだけなのに、その実力差は歴然ですね。 このあたりから、「 計算アルゴリズムっておもしろいなー 」と感じてもらえると幸いです。 一見すると少し難解な計算アルゴリズムでも、自分の手でコードを書いて実装して、高精度な値がバッチリ出た瞬間は、不思議さと楽しさが入り混じって最高にテンションが上がりますよ!
なお、N をさらに 10000 や 100000 まで増やしても、どうしてもラスト2桁の誤差が落ちないのは、 もうそのあたりの桁になると、本来は無限桁まで続く数値を有限桁で打ち切って(丸めて)演算してる誤差など、 数値積分の近似誤差とは別の誤差が効いてくるからです。この類の誤差は演算をくり返すとじわじわ蓄積してくるので、 あまり極端に N を大きく設定したりすると、合っている桁数は逆に減ってしまったりもします。
数値積分などの、近似を用いた数値計算の精度には、アルゴリズム(計算方法)によって決まる本質的な近似の誤差と、 それとは別にコンピューター内での数値の扱いや演算のくり返しによって生じる誤差との、両方が影響してきます。 前者の誤差を抑えるためには刻み数 N を大きくしたいけれども、後者の誤差( や計算所要時間 )を抑えるためにはあまり N を増やしたくない ―― Nの値はその兼ね合いで調整します。アルゴリズムの近似精度の次数が高いと、その妥協点を引き上げるのに有利になります。
[ 数値積分シリーズの連載記事 ]
- 第1回: 矩形法(長方形近似)による数値積分
- 第2回: 台形法(台形近似)による数値積分(前回)
- 第3回: シンプソン法による数値積分(今回)
- 総集編: 積分値を求めるプログラム (数値積分)
ライセンス
このVCSSL/Vnanoコード( 拡張子が「.vcssl」や「.vnano」のファイル )は実質的な著作権フリー(パブリックドメイン) である CC0 の状態で公開しています※。 記事中にC言語/C++/Java言語などでのサンプルコードが掲載されいてる場合は、それらについても同様です。 そのままでのご利用はもちろん、改造や流用などもご自由に行ってください。
※ ただし、このコードの配布フォルダ内には、ダウンロード後すぐに実行できるように、 VCSSLの実行環境も同梱されており、そのライセンス文書は「 License 」フォルダ内に同梱されています (要約すると、商用・非商用問わず自由に使用できますが、使用の結果に対して開発元は一切の責任を負いません、といった具合の内容です)。 配布フォルダ内の各構成物の一覧やライセンスについては「 ReadMe_使用方法_必ずお読みください.txt 」をご参照ください。
※ Vnano の実行環境については、別途スクリプトエンジンのソースコードも一般公開しており、 何らかのソフトウェア内に組み込んでご利用いただく事も可能です。詳細はこちらをご参照ください。
この記事中の商標などについて
- OracleとJavaは、Oracle Corporation 及びその子会社、関連会社の米国及びその他の国における登録商標です。文中の社名、商品名等は各社の商標または登録商標である場合があります。
- Windows は、米国 Microsoft Corporation の米国およびその他の国における登録商標です。この記事は独立著作物であり、Microsoft Corporation と関連のある、もしくはスポンサーを受けるものではありません。
- Linux は、Linus Torvalds 氏の米国およびその他の国における商標または登録商標です。
- その他、文中に使用されている商標は、その商標を保持する各社の各国における商標または登録商標です。
|
角度の「度」とラジアンとを相互変換し、図示もするツール |
|
|
|
45度などの「度」の値と、ラジアンの値とを相互に変換できるツールです。対応する角度の図示もできます。 |
|
FizzBuzz の答えを表示するプログラム |
|
|
|
プログラミングの練習問題としても有名な、FizzBuzz 問題の答えを表示するプログラムの例です。 |
|
Vnano版 | 積分値のグラフ描画用データを出力するプログラム |
|
|
|
数値的に積分を行い、結果の関数をグラフに描くためのデータを出力するコードです。 |
|
Vnano版 | 積分値を求めるプログラム (数値積分) |
|
|
|
矩形法/台形法/シンプソン法を用いて、積分の値を数値的に求めるコードです。 |
|
入力された数式を積分して値とグラフを表示するツール |
|
|
|
画面上で数式を入力すると、それを数値的に積分し、値とグラフを表示してくれるGUIツールです。 |
|
シンプソン法による数値積分 |
|
|
|
積分の値を数値的に求めます。台形法よりも高精度な方法として、被積分関数を微小区間内で二次関数近似して求めた面積を足しあげる、シンプソン法を使用します。 |
|
台形法(台形近似)による数値積分 |
|
|
|
積分の値を数値的に求めます。長方形近似よりも高精度な方法として、台形で近似した微小領域を足しあげる方法を使用します。 |
|
矩形法(長方形近似)による数値積分 |
|
|
|
積分の値を数値的に求めます。長方形の短冊(矩形)で近似した微小領域を足しあげる、最も単純な方法を使用します。 |
|
小数(浮動小数点数)から分数へ近似的に変換するツール |
|
|
|
小数(浮動小数点数)を、適当な誤差の範囲内で、近い分数に変換してくれるツールプログラムです。 |
|
円周率1万桁の計算(ガウス=ルジャンドル法) |
|
|
|
ガウス=ルジャンドル法により、円周率を1万桁まで計算するプログラムです。 |
|
試し割り法による素数判定ツール |
|
|
|
試し割り法を用いて、素数判定を行ってくれる簡易ツールです。 |