» 詳しい使用方法や、エラーで展開できない際の対応方法などはこちら
Vnano版 | 積分値のグラフ描画用データを出力するプログラム
積分の計算を数値的に行い、その過程の値の変化 = 下端Aの設定値を基点とする不定積分の関数の形を、グラフに描くためのデータを出力するプログラムです。 実際にグラフソフトを用いて描く手順についても解説します。
コードは Vnanoで記述していますが、コード解説の項目において、C言語/C++/Java言語で書いたコードも配布しています。 また、Vnano は VCSSL のサブセットであるため、拡張子を変えればそのままVCSSLのコードとしても動きます(その場合、コード先頭の import 文のコメントアウトは外してください)。
なお、今回の内容は前回の続きで、グラフ化用に少し書き変えたものです。 従って、数値積分アルゴリズムの解説等については、まず前回の記事をご参照ください。
使用方法
ダウンロードと展開(解凍)
まず、PC(スマホは未対応)で上の画面の「 ダウンロード 」ボタンを押してください。 するとZIP形式で圧縮されたファイルがダウンロードされます。
その後、ZIPファイルを右クリックして「すべて展開」や「ここに展開」などで展開(解凍)してください。 展開が成功すると、ZIPファイルと同じ名前のフォルダができ、その中にZIPファイルの中身が入っています。
» 展開がエラーで止まってしまう場合や、ファイル名が文字化けしてしまう場合は…
プログラムの起動
Windows をご使用の場合
上記でZIPファイルを展開したフォルダ内にある、以下のバッチファイルをダブルクリック実行してください:
もしプログラムを書き変えながら使いたい場合は、代わりに「 VCSSL_Editor__プログラム編集はこちら.bat 」を実行してください。
正常に起動できると、初回のみ、Java実行環境を入手するか等を尋ねられるので、適時答えて済ませると、プログラムが起動します。 2回目以降はすぐに起動します。
Linux 等をご使用の場合
ZIPファイルを展開したフォルダ内へコマンドライン端末で cd して、以下の通り入力して実行してください:
(プログラムの内容を書き変えながら使いたい場合は、代わりに VCSSL_Editor.jar を実行)
» javaコマンドが使用できない等のエラーが表示される場合は…
起動後
グラフ化用データの表示、またはファイルへの保存
起動すると、まず黒いウィンドウ(VCSSLコンソール)が表示されて計算処理が始まり、 その画面上にグラフ用データが書き出されていきます:
※ 画面の様子はOSや環境によって異なります。 数値の桁数がところどころ不揃いなのは、演算や2進10進変換(下記参照) による微小誤差を丸めずに、そのまま出力しているためです。 綺麗にしたい場合は round 関数で丸められますが、今回は人間が読むのではなくてグラフソフトに渡すデータなので、余分な加工はしないままにしています。
※ 数値は内部的には2進数で処理されますが、人間が読み書きする主に10進数なので、プログラム解釈時や表示時に両者間の変換が行われ、浮動小数点数(float/double)では値によってはそこで誤差が生じます。
データ内には、グラフに描く座標値が、一行につき一点ずつ「 x y 」とタブ空白区切りで記載されています。
計算が完了すると、黒い画面へのデータ書き出しも止まります(標準では一瞬で終わります)。 ここで 画面上部のメニューバーから「 File 」>「 Save File ... 」を選択すると、 表示されたデータをファイルに保存できます。
表示/保存したデータからグラフを描く方法や、描かれたグラフが数値的 & 数式的に何を意味しているのかについては、グラフの描画方法 の項目をご参照ください。
被積分関数(積分対象の関数)や積分区間などの変更
積分内容を変更するには、スクリプト「 IntegralForPlot.vnano 」内で宣言されている、 関数 f(x) の内容や変数 A, B の値、および数値積分の区間分割数 N(前回の記事参照)の値を書き変えてください。 標準では x*cos(x) を x = 0 から 30 までの区間で積分(グラフが絵的に面白いため)するようになっています。
// =======================================================================
// 以下、積分内容の設定
// =======================================================================
double A = 0.0; // 積分区間の下端 (x軸上の左端)
double B = 1.0; // 積分区間の上端 (y軸上の左端)
int N = 10000; // 数値積分における区間分割数 (刻み数)
// 被積分関数 (積分対象の関数)
double f(double x) {
return cos(x);
}
グラフ用のデータ出力設定の変更
同様にスクリプト内で宣言されている変数 PRINT_POINTS で、グラフにプロット(描画)したい座標点の数を指定できます。
// =======================================================================
// 以下、データ出力関連の設定
// =======================================================================
int PRINT_POINTS = 1000; // 出力する座標点の数 (グラフのプロット点数)
int PRINT_INTERVAL = N / PRINT_POINTS; // [自動設定] ループ内での出力周期
// ※ 実際の点数は、最終値を別途出力するため、上記から1点だけ多くなります。
// また、N が PRINT_POINTS で割り切れない場合、点数は多少増減します。
ただし、この設定値の効き方は厳密ではなく、ある程度の誤差が入る場合があります。 あくまでもグラフの点密度を調整する目安程度に捉えて設定してください(詳しくは コード解説のこの項目 参照)。
計算アルゴリズムの切り替え
アルゴリズムは、矩形法、台形法、シンプソン法を使用できます。 スクリプト内で、それぞれのアルゴリズムによる計算行が書かれています。 それらの行の先頭に、行を読み飛ばす記号「 // 」を付け外しして、使うアルゴリズムを選択してください (各アルゴリズムの詳細は前回の記事参照)。 標準ではシンプソン法が使用されます。
// -------------------------------------------------------------------
// 以下、i 番目の微小区間の面積を求め、積分値に加算 (どれか 1 つ選択)
// -------------------------------------------------------------------
// 矩形法 (長方形で近似した微小領域の面積を足す)
// value += f(x) * delta;
// 台形法 (台形で近似した微小領域の面積を足す)
// value += ( f(x) + f(x+delta) ) * delta / 2.0;
// シンプソン法 (二次関数で近似した微小領域の面積を足す)
value += ( f(x) + f(x+delta) + 4.0 * f(x+delta/2.0) ) * delta / 6.0;
グラフの描画方法
VCSSLランタイムでの場合(今の手順での場合はこちら)
このページからダウンロードしたパッケージでは、実行用にVCSSLランタイム(※コード同梱配布用のコンパクト版)というソフトが使われます。 VCSSLランタイムでは、黒い画面に表示されたデータをグラフ化する機能が標準搭載されているため、何も用意せにグラフを描画できます。
具体的には、計算完了後、黒い画面上部のメニューバーから「 File 」>「 Plot Graph2D ... 」を選択すると…
すると、以下のようにグラフが表示されます:
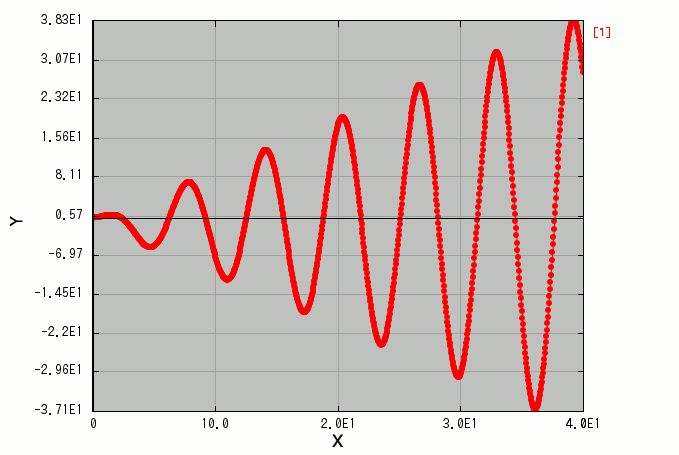
※ X/Y軸範囲や目盛り数値の書式設定、点を打つか/線で繋ぐかどうか等の設定は、グラフ画面上部のメニューバーから行えます。 グラフを資料で使う場合などには、そういった見栄えの調整を行ってください。 標準では上のように、単純にX/Y軸範囲はデータの最大最小値そのものに設定され、座標上に点が打たれて、データ内での登場順に線で繋がれます。 これはデータのありのままを把握するのには好都合なので、自動で見栄え用の調整等はされないようになっています。
このグラフが、プログラム内で指定された関数 f(x) を、下端 A(プログラム内で指定)から数値的に積分していって、 その過程の値変化(= x に対する積分結果の関数の形)を、横軸を x にとってプロットしたものとなっています。 これは A を基点とする不定積分 と呼ばれるもので※、数式で表すと:
\[ F(x) = \int^x_A f(t) dt \]
をプロットしている事になります。
上のグラフでプロットした例の場合、積分する関数はデフォルト設定の \(f(x) = x \cos x\) で、下端は A = 0 なので、 理論上の正しい結果は
\[ F(x) = \int^x_0 t \cos t dt = \big[ t \sin t + \cos t \big]^x_0 = x \sin x + \cos x + 1 \]
です。 上のグラフにプロットしたデータは、数値積分誤差を除けばほぼ上の式の通りの結果※になっています。
関数電卓 RINPn を使っている場合
関数電卓ソフトの RINPn では、Vnanoのプログラムは実行できますが、グラフ表示機能は現時点では標準搭載されていません。 そこで、別途グラフソフトを用意し、組み合わせて使用します。 今回のプログラムが出力するデータは、結構スタンダードな形式なので、gnuplot などの色々なグラフソフトで描画できます。
ここでは例として、VCSSL や Vnano、RINPn と同じ開発元(つまりうちです)のグラフソフトである「 リニアングラフ 」を使ってみましょう。 2D版と3D版がありますが、今回は2D版を使用します:
- リニアングラフ2D 公式サイト(日本語ページ)
- https://www.rinearn.com/ja-jp/graph2d/
リニアングラフを起動すると、先に扱ったVCSSLランタイムの場合と全く同じグラフ画面が立ち上がります。 それもそのはず、VCSSLランタイムに標準搭載されていたグラフ機能の中身もリニアングラフだからです。
グラフの描画方法は簡単です。 まずは普通に RINPn で今回のプログラムを実行しましょう。 プログラムのファイル「 IntegralForPlot.vnano 」を RINPn のフォルダ内に置いて、 RINPn の電卓画面のINPUT項目に、このファイル名をそのまま入力します。 すると黒い画面が表示され、そこにグラフ用のデータが出力されます:
この黒い画面のデータを全行選択(マウスでドラッグしてもいいですが、Ctrl+Aキーの同時押しもで可能です)した状態で、右クリックメニューからコピーし、 そしてリニアングラフ2Dの画面上で右クリックして「 データの貼り付け 」を行うと、グラフが表示されます:

VCSSLランタイムの場合と同じグラフですね。 どちらも内部で同じスクリプトエンジン(Vnanoエンジン)を使って計算処理を行っていて、 それを実質同じグラフソフトで描画しているため、どちらを使っても完全に同一のグラフが得られます。
RINPn を使ってコマンドラインで実行する場合
RINPn は、「 bin 」フォルダのパスをOSの環境変数 Path/PATH に登録すると「 rinpn 」コマンドが使用できます。 その場合はリニアングラフの bin フォルダのパスも一緒に登録しておくと、こちらも「 ring2d 」コマンド(3Dの場合は ring3d )が使えるようになり、 両者を組み合わせるのに便利です。実際、今の場合の例では、コマンドラインで:
rinpn IntegralForPlot.vnano > data.txt
ring2d data.txt
とすると、計算結果がファイル data.txt に保存された上で、その内容がグラフとして表示されます。 表示されるグラフの内容は、上で掲載したものと全く同じです。
RINPn をコマンドラインで使いつつ、描画に gnuplot を使いたい場合
余談ですが、グラフ描画に gnuplot を使いたいという場合は:
rinpn IntegralForPlot.vnano > data.txt
gnuplot
(ここでgnuplotが起動します)
plot "data.txt" with lp pt 7 ps 0.5
(使い終わったら)
quit
などとします。「 with lp 」が線とマーカー(点)でのプロット、「 pt 7 」がマーカーを丸い点にする指定(環境やバージョンによっては別の数字かもしれません)、「 ps 0.5 」がそのサイズ指定です。 表示されるグラフは:
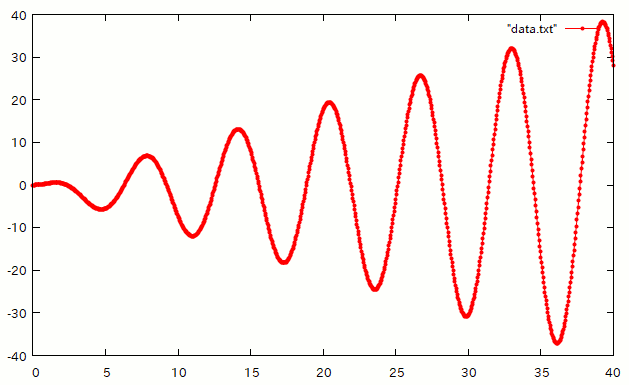
この通りです。細かい見栄えは違いますが、グラフの形としては先ほどのリニアングラフ2Dの場合と同じですね。 このように、今回のコードで出力されるような書式のデータ(各行に1座標点ずつ x y と並べたデータ)は、色々なグラフソフトでプロットできます。
コード解説
コード全体
このプログラムのコードはVnanoで記述されています。 VnanoはC言語系のシンプルな文法を持っているので、C系の言語に触れられた事のある方なら、 コメントを参考にしながらコード内容を比較的簡単に追う or 改造する事ができると思います。
まずは、コード全体を見てみましょう:
coding UTF-8; // 文字コード宣言 (文字化け予防)
// import Math; // VCSSLでは必要 (Vnanoでは実行ソフト側で必要に応じて設定)
// =======================================================================
// 以下、積分内容や出力関連の設定
// =======================================================================
// 被積分関数 (積分対象の関数)
double f(double x) {
return x * cos(x);
}
double A = 0.0; // 積分区間の下端 (x軸上の左端)
double B = 40.0; // 積分区間の上端 (y軸上の左端)
int N = 10000; // 数値積分における区間分割数 (刻み数)
// =======================================================================
// 以下、データ出力関連の設定
// =======================================================================
int PRINT_POINTS = 1000; // 出力する座標点の数 (グラフのプロット点数)
int PRINT_INTERVAL = N / PRINT_POINTS; // [自動設定] ループ内での出力周期
// ※ 実際の点数は、最終値を別途出力するため、上記から1点だけ多くなります。
// また、N が PRINT_POINTS で割り切れない場合、点数は多少増減します。
// =======================================================================
// 以下、積分の値を数値的に求める処理
// =======================================================================
double delta = (B - A) / N; // 足し上げる微小区間の幅 (刻み幅)
double value = 0.0; // この変数に積分値を足し上げていく
// 積分区間をN分割した微小区間を、左(下端)から右(上端)へ順に辿るループ
for(int i=0; i<N; ++i) {
// i 番目の微小区間における、左端の x 座標値を求める
double x = A + i * delta;
// 設定周期ごとに、グラフにプロットするための座標値を出力する
if (i % PRINT_INTERVAL == 0) {
println(x, value);
}
// -------------------------------------------------------------------
// 以下、i 番目の微小区間の面積を求め、積分値に加算 (どれか 1 つ選択)
// -------------------------------------------------------------------
// 矩形法 (長方形で近似した微小領域の面積を足す)
// value += f(x) * delta;
// 台形法 (台形で近似した微小領域の面積を足す)
// value += ( f(x) + f(x+delta) ) * delta / 2.0;
// シンプソン法 (二次関数で近似した微小領域の面積を足す)
value += ( f(x) + f(x+delta) + 4.0 * f(x+delta/2.0) ) * delta / 6.0;
}
// 最後の一点を出力
println(B, value);
今回のコードは、前回のコードに、グラフ用のデータ出力処理を書き足したものになっています。 そういう意味では今回のコードがあれば全て事足りる気もするのですが、 「 値を求めたいのか、グラフを描きたいのか 」という用途の微妙な違いと、 記事での解説ボリュームの都合で、2回に分けて扱っています。
従って、上のコード内容がやや複雑に感じる方は、 先に前回のコード解説を読まれた方がスムーズかもしれません。 前回の記事では、矩形法/台形法/シンプソン法など、数値積分のアルゴリズムも踏まえて解説しています。 今回はそこは割愛し、そこから書き加えた、グラフ用のデータ出力処理の部分をメインに説明します。
それでは、今回のコード内容を追っていきます。
コード先頭
まずは先頭部分です。 ここは、このプログラムの目的の処理とは無関係なため、そちらに興味がある場合は読み飛ばしても大丈夫です。 一応ですが、ここで行っている事は以下の通りです:
coding UTF-8; // 文字コード宣言 (文字化け予防)
// import Math; // VCSSLでは必要 (Vnanoでは実行ソフト側で必要に応じて設定)
最初の「 coding 〜 」の行では、文字化け対策で、プログラムのファイルが「UTF-8」という文字コードで書かれている事を表しています。
続く「 import 〜 」の行は、簡単に言うと、このコードで数学関数を使う事を宣言しています(Vnanoでは、アプリ側でライブラリ読み込み設定を行うため、必須ではありません)。
被積分関数(積分対象の関数)や積分区間などの定義
その後に、被積分関数や積分区間、および数値積分用のパラメータを定義している箇所が続きます:
// =======================================================================
// 以下、積分内容の設定
// =======================================================================
double A = 0.0; // 積分区間の下端 (x軸上の左端)
double B = 1.0; // 積分区間の上端 (y軸上の左端)
int N = 10000; // 数値積分における区間分割数 (刻み数)
// 被積分関数 (積分対象の関数)
double f(double x) {
return cos(x);
}
積分内容を変える際は、ここの内容を変更してください。 基本的には上記のコード内コメントの通り、積分したい関数をそのままコード内の f(x) 関数として定義し、 積分区間下端の x 値を変数 A に、上端の x 値を変数 B に設定します。
N については、数値積分における微小区間の分割数(いわゆる "刻み" の数)で、 詳細はこの次の項目参照なのですが、基本的には大きいほど精度が上がる半面、計算時間が増えます。 ただしあまり大きくすると、計算ループ回数が増え、丸め誤差やその他微小誤差の蓄積的な寄与が逆に増大してしまうため、 ほどほどの大きさの範囲で、アルゴリズムを切り替えながら、必要な桁まで信頼できる値が出ていると判断できるあたりに設定します(関数の凹凸の激しさ等によって異なります)。 詳細は前回の記事のコード解説をご参照ください。
データ出力の設定値の定義
続いて、グラフ用のデータを出力する際の設定部分です。ここは前回のコードには無く、今回書き加えられた箇所です。
// =======================================================================
// 以下、データ出力関連の設定
// =======================================================================
int PRINT_POINTS = 1000; // 出力する座標点の数 (グラフのプロット点数)
int PRINT_INTERVAL = N / PRINT_POINTS; // [自動設定] ループ内での出力周期
// ※ 実際の点数は、最終値を別途出力するため、上記から1点だけ多くなります。
// また、N が PRINT_POINTS で割り切れない場合、点数は多少増減します。
コード内コメントの通り、変数 PRINT_POINTS に、グラフにプロット(描画)したい座標点の数を指定します。 関数の凹凸の激しさや、点を打つのか線を描くのか※にもよりますが、大体数百〜数千点くらいが目安です。
ただし、この設定値の効き方は厳密ではなく、ある程度の誤差が入る場合があります。 あくまでもグラフの点密度を調整する目安程度に捉えて設定してください。
積分値を計算しながらデータを出力しているループ部分
その後がいよいよこのスクリプトの中心的な処理である、「 積分の値を数値的に求める 」計算ループの部分です:
// =======================================================================
// 以下、積分の値を数値的に求める処理
// =======================================================================
double delta = (B - A) / N; // 足し上げる微小区間の幅 (刻み幅)
double value = 0.0; // この変数に積分値を足し上げていく
// 積分区間をN分割した微小区間を、左(下端)から右(上端)へ順に辿るループ
for(int i=0; i<N; ++i) {
// i 番目の微小区間における、左端の x 座標値を求める
double x = A + i * delta;
// 設定周期ごとに、グラフにプロットするための座標値を出力する
if (i % PRINT_INTERVAL == 0) {
println(x, value);
}
// -------------------------------------------------------------------
// 以下、i 番目の微小区間の面積を求め、積分値に加算 (どれか 1 つ選択)
// -------------------------------------------------------------------
// 矩形法 (長方形で近似した微小領域の面積を足す)
// value += f(x) * delta;
// 台形法 (台形で近似した微小領域の面積を足す)
// value += ( f(x) + f(x+delta) ) * delta / 2.0;
// シンプソン法 (二次関数で近似した微小領域の面積を足す)
value += ( f(x) + f(x+delta) + 4.0 * f(x+delta/2.0) ) * delta / 6.0;
}
この部分で行っている処理の詳細については、前回の記事のコード解説をご参照ください。
ものすごく要約すると、ここでは下端 A から上端 B までの範囲で、f(x) と x 軸との間の面積( = A から B までの定積分値)を近似的に求めています。 その方法は、一番簡単な矩形法では下図のイメージで、A から B までの範囲を細かい微小区間に刻み、それらの面積を長方形と見なして求め、for 文で足し上げています。
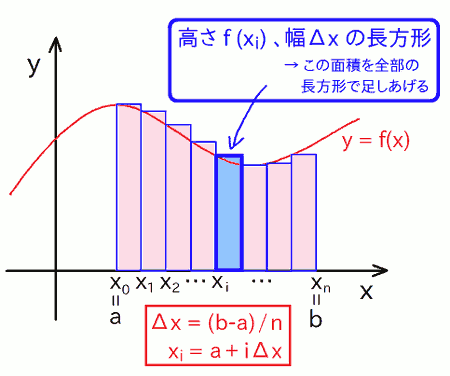
この微小区間の面積を長方形で近似するのが矩形法(上図)、台形で近似するのが台形法、そして上側の線を二次関数で曲線的に近似するのがシンプソン法です。 それぞれ精度が劇的に違い、前回はそのあたりを重点的に見比べました。
ただ、前回は A から B までの最終的な定積分の値 (1個) を求めるのが目的であったため、for 文の中では何も出力していませんでした。 今回は、その計算ループの途中の値を、 定期的に「 その時点のx その時点の積分値 」の形(行内容)で出力しています:
// 積分区間をN分割した微小区間を、左(下端)から右(上端)へ順に辿るループ
for(int i=0; i<N; ++i) {
// i 番目の微小区間における、左端の x 座標値を求める
double x = A + i * delta;
// 設定周期ごとに、グラフにプロットするための座標値を出力する
if (i % PRINT_INTERVAL == 0) {
println(x, value);
}
// -------------------------------------------------------------------
// 以下、i 番目の微小区間の面積を求め、積分値に加算 (どれか 1 つ選択)
// -------------------------------------------------------------------
...
}
上の45行目がその出力処理で、この println 関数は、引数に( , 区切りで)指定された値を、 タブ空白区切りで 1 行にして、データ表示用の黒い画面※に書いてくれます。 その内容が、グラフソフトでは「 x座標 y座標 」と解釈され、1 点が描画されます。
それを for 文で繰り返しているので、黒い画面に行が流れるように複数ダーッと書かれて、グラフ上ではたくさん点が描画されたわけです。
さて、今のアルゴリズムでは、上記の for 文で x 軸上を下端 A から上端 B の方に向かって(先の図で左から右に向かって)移動しながら、微小区間の面積を 1 個ずつ変数 value に積算していっています。 という事は、その途中での、x がある適当な値の時には、その x よりも左側にある領域の面積(近似値)が、 value の値として求まっているはずです。 それはまさに冒頭にも登場した、A を起点とする不定積分:
\[ F(x) = \int^x_A f(t) dt \]
の、x における値という事になります。 そして、x の値はループ毎に左から右へ動いていくので、それを横軸の値として、上の積分値(≒ value の値)を縦軸 y に書いていけば、 上の関数のグラフを(近似的に)描けるというわけです。
最終値を出力する部分
ところで、上で見た for 文の計算ループでは、ループの先頭で x と value の値を出力しています。 これはつまり、「 i 番目の微小区間の左端の x の値と、その面積を足す前の value の値 」を出力している事になります。 この「 足す前の 」という点が一見奇妙に見えるかもしれません。 確かにデバッグ時に「 i 番目のループまでの積算値を知りたい 」といった場合にはおかしいです。
ところが、いまは「 ある x において、それより左にある微小面積を全て足した値を y に出力する 」というのが目的です。 x の値は i 番目の微小区間の左端、それは即ち直前に足した微小区間の右端の値なので、 紙に図などを描いてよく考えると、今回の目的ではこのタイミングで出力して正解(value が下端から x までの積算値になる)という事になります。
ただ、上の出力処理だけでは、一つ抜けがあります。 というのも、ループ先頭で、常に 微小面積を足す前の値 を出力しているという事は、 ぜんぶ足した値、つまり x が積分の上端 B に達した時点での値が出力されない事になってしまうからです。 そもそも x も微小区間「左端」の値で、最後の微小区間の左端は B よりも幅 1 個分足りないので、やはり最後の点は抜けてしまう事がわかります。
そこで、計算ループが終わった後の value には A から B までの全面積を足した値が入っているはずなので、それを出力しています。 その際、x 座標値は B の値そのものとしています。
// 最後の一点を出力
println(B, value);
こうすると、データの最終行の右列の値を見る事で、A から B までの定積分の値も知る事ができ、前回のコードと同じ用途もこなせます。
最後に
今回の内容は以上です。
余談ですが、個人的に、過去につまらいと思っていたものが、グラフを描いてみるとなんだか面白く思えるようになって、熱が入った事がしばしばあります。 グラフにはそういう不思議な魅力があるのかもしれません。 というよりも、プログラムを使って絵的なものを表示するという事自体が、表示された瞬間にテンションが上がって、作業者を楽しくしてくれる効果があるような気がします。 今回の計算結果のグラフが表示された時に、そういう雰囲気を共感してもらえると嬉しいのですが、果たしてどうだったでしょうか。
ライセンス
このVCSSL/Vnanoコード( 拡張子が「.vcssl」や「.vnano」のファイル )は実質的な著作権フリー(パブリックドメイン) である CC0 の状態で公開しています※。 記事中にC言語/C++/Java言語などでのサンプルコードが掲載されいてる場合は、それらについても同様です。 そのままでのご利用はもちろん、改造や流用などもご自由に行ってください。
※ ただし、このコードの配布フォルダ内には、ダウンロード後すぐに実行できるように、 VCSSLの実行環境も同梱されており、そのライセンス文書は「 License 」フォルダ内に同梱されています (要約すると、商用・非商用問わず自由に使用できますが、使用の結果に対して開発元は一切の責任を負いません、といった具合の内容です)。 配布フォルダ内の各構成物の一覧やライセンスについては「 ReadMe_使用方法_必ずお読みください.txt 」をご参照ください。
※ Vnano の実行環境については、別途スクリプトエンジンのソースコードも一般公開しており、 何らかのソフトウェア内に組み込んでご利用いただく事も可能です。詳細はこちらをご参照ください。
この記事中の商標などについて
- OracleとJavaは、Oracle Corporation 及びその子会社、関連会社の米国及びその他の国における登録商標です。文中の社名、商品名等は各社の商標または登録商標である場合があります。
- Windows は、米国 Microsoft Corporation の米国およびその他の国における登録商標です。この記事は独立著作物であり、Microsoft Corporation と関連のある、もしくはスポンサーを受けるものではありません。
- Linux は、Linus Torvalds 氏の米国およびその他の国における商標または登録商標です。
- その他、文中に使用されている商標は、その商標を保持する各社の各国における商標または登録商標です。
|
角度の「度」とラジアンとを相互変換し、図示もするツール |
|
|
|
45度などの「度」の値と、ラジアンの値とを相互に変換できるツールです。対応する角度の図示もできます。 |
|
FizzBuzz の答えを表示するプログラム |
|
|
|
プログラミングの練習問題としても有名な、FizzBuzz 問題の答えを表示するプログラムの例です。 |
|
Vnano版 | 積分値のグラフ描画用データを出力するプログラム |
|
|
|
数値的に積分を行い、結果の関数をグラフに描くためのデータを出力するコードです。 |
|
Vnano版 | 積分値を求めるプログラム (数値積分) |
|
|
|
矩形法/台形法/シンプソン法を用いて、積分の値を数値的に求めるコードです。 |
|
入力された数式を積分して値とグラフを表示するツール |
|
|
|
画面上で数式を入力すると、それを数値的に積分し、値とグラフを表示してくれるGUIツールです。 |
|
シンプソン法による数値積分 |
|
|
|
積分の値を数値的に求めます。台形法よりも高精度な方法として、被積分関数を微小区間内で二次関数近似して求めた面積を足しあげる、シンプソン法を使用します。 |
|
台形法(台形近似)による数値積分 |
|
|
|
積分の値を数値的に求めます。長方形近似よりも高精度な方法として、台形で近似した微小領域を足しあげる方法を使用します。 |
|
矩形法(長方形近似)による数値積分 |
|
|
|
積分の値を数値的に求めます。長方形の短冊(矩形)で近似した微小領域を足しあげる、最も単純な方法を使用します。 |
|
小数(浮動小数点数)から分数へ近似的に変換するツール |
|
|
|
小数(浮動小数点数)を、適当な誤差の範囲内で、近い分数に変換してくれるツールプログラムです。 |
|
円周率1万桁の計算(ガウス=ルジャンドル法) |
|
|
|
ガウス=ルジャンドル法により、円周率を1万桁まで計算するプログラムです。 |
|
試し割り法による素数判定ツール |
|
|
|
試し割り法を用いて、素数判定を行ってくれる簡易ツールです。 |