入力された数式を積分して値とグラフを表示するツール

このVCSSLプログラムは、 画面上で数式を入力すると、それを数値的に積分し、 値とグラフを表示してくれるGUIツールです。 数値積分のアルゴリズムは、 シンプソン法、 台形法、および 矩形法（長方形近似） から選択できます。

[ 数値積分シリーズの連載記事 ]

• 第1回： 矩形法（長方形近似）による数値積分
• 第2回： 台形法（台形近似）による数値積分
• 第3回： シンプソン法による数値積分
• 応用 ： 入力された数式を積分して値とグラフを表示するツール（今回）

スポンサーリンク

---

使用方法

ダウンロードと展開（解凍）

まず、PC（スマホは未対応）で上の画面の「 ダウンロード 」ボタンを押してください。 するとZIP形式で圧縮されたファイルがダウンロードされます。

その後、ZIPファイルを右クリックして「すべて展開」や「ここに展開」などで展開（解凍）してください。 展開が成功すると、ZIPファイルと同じ名前のフォルダができ、その中にZIPファイルの中身が入っています。

» 展開がエラーで止まってしまう場合や、ファイル名が文字化けしてしまう場合は…

プログラムの起動

Windows をご使用の場合

上記でZIPファイルを展開したフォルダ内にある、以下のバッチファイルをダブルクリック実行してください：

もしプログラムを書き変えながら使いたい場合は、代わりに「 VCSSL_Editor__プログラム編集はこちら.bat 」を実行してください。

正常に起動できると、初回のみ、Java実行環境を入手するか等を尋ねられるので、適時答えて済ませると、プログラムが起動します。 2回目以降はすぐに起動します。

» うまく起動できずにエラーになってしまう場合は…

Linux 等をご使用の場合

ZIPファイルを展開したフォルダ内へコマンドライン端末で cd して、以下の通り入力して実行してください：

» javaコマンドが使用できない等のエラーが表示される場合は…

起動後

画面の様子

起動すると、まず2つの画面が立ち上がります。 背後の黒いウィンドウがコンソール画面、手前の左にある白いウィンドウが入力画面です。 入力画面上の「 CALC - 計算 」ボタンを押すと、さらにグラフ画面(右)が起動します。

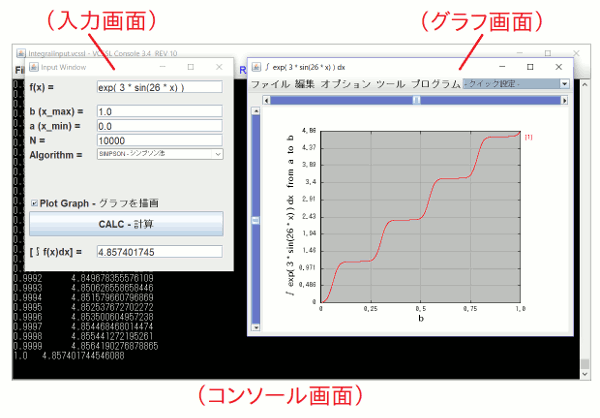
数式と積分区間を入力して積分する

まず、積分したい数式（被積分関数）を、入力画面の「 f(x) = 」の入力欄に入力してください。 式の書き方のポイントは以下の通りです：

数式を入力したら、続いて「 b (x_max) = 」および「 a (x_min) = 」の入力欄に、それぞれ積分区間の上端および下端の値を入力してください。 必要なら、ここでも数式や sin や cos などの数学関数を使用する事ができます。また、円周率の値は「 PI 」として使用できます。

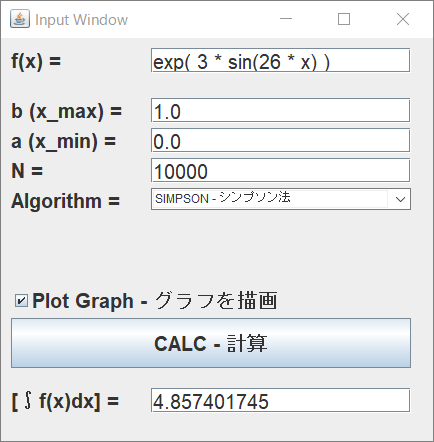
数式と積分区間を入力したら、 入力画面の「 CALC - 計算 」ボタンを押すと、その数式を積分する計算が実行され、結果の値がボタンの下に表示されます。 積分結果の値は、10桁に丸めて表示されます（ 丸めていない元の値は、コンソール画面（黒い画面）の最終行の右の列の値から確認できます ）。

グラフの描画

上記の通り「 CALC - 計算 」ボタンを押した時点で、 積分区間の上端 b の値を、下端 a から指定値まで動かした、積分過程のグラフも表示されます。 横軸が b の値、縦軸が積分値です。下端 a の値は、グラフ上では横軸の最小値(左端)の値として確認できます。 このグラフはつまるところ、被積分関数 f(x) を積分した関数 F(x) + C を、横軸を x として描いたグラフと同じ形をしています（ただし、a の設定値に応じて、上下に平行移動されています）。

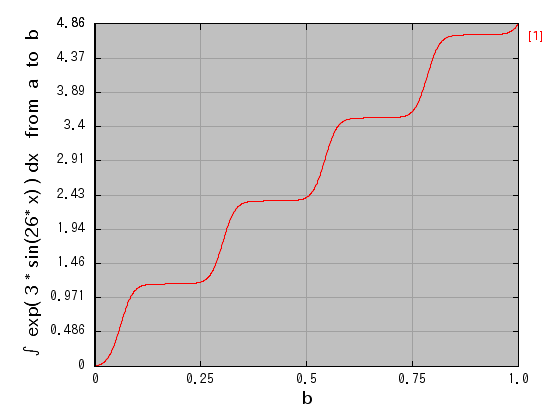
グラフの目盛りや範囲などを綺麗に揃えたい場合や、ラベルやタイトルを編集したい場合などは、グラフ画面上部のメニューバーから細かい調整を行う事ができます。

なお、後述する N の設定値によっては、グラフ用のデータを用意する処理に時間がかかるため、 大きいNの設定で使っていて、重いと感じたら「 Plot Graph - グラフを描画する 」のチェックを外してください。 そうするとグラフは描かれなくなりますが、計算は素早く完了するようになります。

ただ、本質的な積分可能性（リーマン可積分かどうか）にも関わる問題として、被積分関数が無限大に発散している箇所があったりすると積分も吹っ飛んでおかしくなったり、 また、滑らかでない関数の場合は積分値が収束しない場合もあります。 従って、初めて積分する数式は、 一度は粗い N でグラフを描いてみて、そもそも積分値が収束しそうなのかを確認する事をお勧めします。 積分ではなく元の関数のグラフも確認したい場合は、 「 y = f(x) の形の数式を2Dグラフとして描画するツール 」も併せてご利用ください。

数値積分アルゴリズムの選択と、刻み数 N の設定

さて、数値的に積分を計算する際に、精度を左右する重要なテーマが、 数値積分アルゴリズムの選択と、刻み数 N の値をどれくらいにするかです。 このプログラムでは、数値積分アルゴリズムは入力画面上の「 Algorithm = 」の選択欄で、 N の値は「 N = 」の入力欄で指定できます。 以下では、そもそもそれらのアルゴリズムや N の値が、どういう意味のものなのかについて、簡単に説明します。

このプログラムでは、シンプソン法、台形法（台形公式）、および矩形法（長方形近似）の3つをサポートしています。 各アルゴリズムについては、下記の記事でもそれぞれ個別に解説していますので、詳しく読みたい場合はそちらをご参照ください：

• 矩形法（長方形近似）による数値積分
• 台形法（台形近似）による数値積分
• シンプソン法による数値積分

ここでは、簡単なイメージを駆け足で見てみましょう。 まず前提として、被積分関数 f(x) を、a から b までの区間で定積分した値は、下図のように、その区間内で f(x) と x 軸に挟まれた領域の面積に相当します。 従って、この面積を求めれば、積分値が得られるわけです。

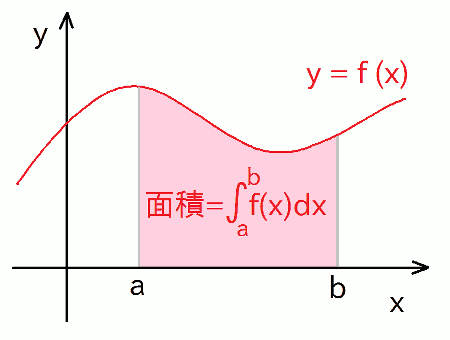
矩形法（長方形近似）

一番単純な数値積分アルゴリズムである矩形法（長方形近似）では、この面積を、微小な N 個の領域に区切って、その微小領域の面積を長方形で近似します。 そして、その N 個の微小領域の長方形を並べて、それらの面積を足す事で、積分区間全体での面積を求めます。イメージとしては下図の通りです。

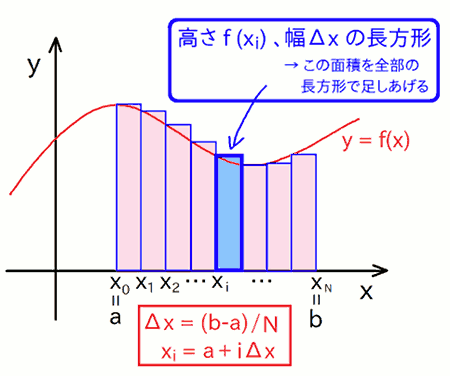
上の図から、積分区間を微小領域で刻む数 N を増やしたほうが、微小領域の刻みが細かくなって、 上のギザギザではみ出したり欠けている箇所が減り、 f(x) と x 軸との間の面積をよく近似できるようになりそうな事が想像できると思います。 これは実際その通りで、矩形法では、N を1桁増やすと、積分値の信頼できる桁数がだいたい 1 桁程度増える事が見込めます。

台形法（台形公式）

続いて台形法です。これは上で説明した矩形法をちょっとだけ改良したもので、長方形の上の辺を、f(x) の変化に沿うように傾けます。これによって長方形は台形になりますね。 あとは、N 個の微小領域の台形を並べて、それらの面積を足す事で、積分区間全体での面積を求めます。イメージは下図です。

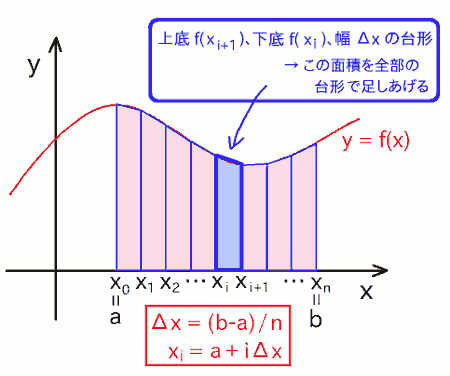
上図を見ると、最初の矩形法の場合と比べて、ギザギザにはみ出したり欠けたりしていた部分が軽減されて、直感的にも面積の近似精度が上がっていそうに見えます。 実際その通りで、台形法では、N を1桁増やすと、積分値の信頼できる桁数がだいたい 2 桁程度増える事が見込めます。

ただ、台形法では微小領域の上の辺を直線で近似しているので、f(x) の微妙な丸みなどは真似しきれません。f(x) が直線でもない限り、 拡大すると少し面積が食い違っているはずです（下図）。これが台形法の誤差を生み出しています。

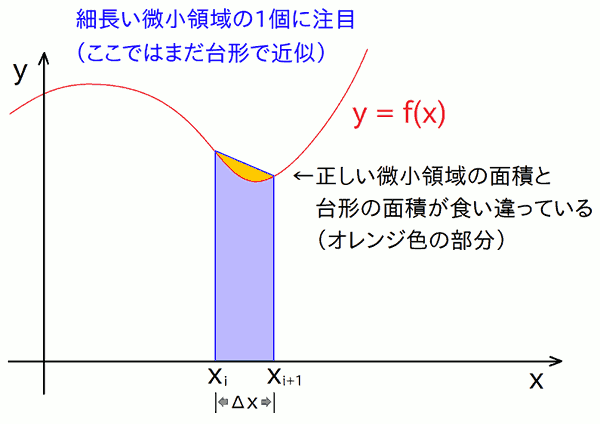
シンプソン法

「 それなら、上の辺を曲線で近似すれば、もっと精度が上がるのでは？ 」と思いませんか？ …という事で、上図の台形の上の辺を、f(x) の丸みに良い感じでフィットする二次関数で置き換えたのがシンプソン法です。下図の通りです。

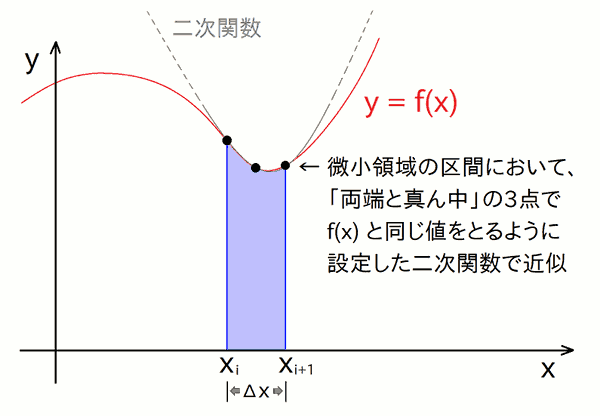
シンプソン法では、この「 上の辺を二次関数でかじった短冊のようなもの 」を N 個並べる事で、面積を足し上げて積分値を求めます。 f(x) の丸みをそれなりに（2次成分まで）真似できるので、少なくとも直線で真似る台形法よりは精度が上がりそうですね。 実際その通りで、シンプソン法では N を1桁増やすと、積分値の信頼できる桁数がだいたい 4 桁程度増える事が見込めます。 台形法は2桁程度だったので、だいぶ違いますね。 （ 一方で、被積分関数 f(x) とアルゴリズムとの相性問題のようなものもあり、必ずしも高次のアルゴリズムが万能とも言い切れないのも複雑なところです。）

と、やや長い前置きになってしまいましたが、数値積分アルゴリズムと N のイメージが大まかには掴めたでしょうか。

刻み数 N の調整とアルゴリズム選択

さて、重要なのは N の値です。 N は、あくまでも基本的にですが、大きいほうが上述の近似精度が向上し、誤差（厳密な積分値と、計算結果の値のずれ）が減る事が見込めます。 ただし、あまり極端に増やし過ぎると、逆に別の誤差※ が効いてきてしまったりもするので、N を1桁ずつ変えながら何度か計算してみて、 積分値が概ね（求める値の桁数まで）収束しているあたりに設定するのが無難です。具体的な適正範囲は被積分関数 f(x) の凹凸の激しさなどによって異なります。

N を1桁増やすと、結果の信頼できる桁数が何桁増えるかは、既に述べた通り、アルゴリズムによって大きく異なります。 基本的には、矩形法よりも台形法の方が、また台形法よりもシンプソン法の方が、精度を出すのに有利な場面が多いでしょう。 一方で、先に少し述べた通り、被積分関数 f(x) とアルゴリズムとの相性問題のようなものもあるので、 初めて積分する関数で、精度が要求される場合には、色々変えて様子を掴むのがおすすめです。

---

スポンサーリンク

---

コード解説

コード全体

このプログラムのコードはVCSSLで記述されています。 VCSSLはC言語系のシンプルな文法を持っているので、C系の言語に触れられた事のある方なら、 コメントを参考にしながらコード内容を比較的簡単に追う or 改造する事ができると思います。

今回のコードは、数値積分の計算処理に、GUIの画面を組み合わせて、ツールとして仕上げたものです。 数値積分のアルゴリズムをシンプルに実装したプログラムについては、以下の回で解説していますので、そちらをご参照ください：

[ 数値積分のアルゴリズム解説記事（連載） ]

• 第1回： 矩形法（長方形近似）による数値積分
• 第2回： 台形法（台形近似）による数値積分
• 第3回： シンプソン法による数値積分

また、VCSSLでのGUI画面の構築については、「 VCSSL GUI開発ガイド 」をご参照ください。

今回のコードは、サンプルコードというよりは実際に使うためのツールなので、 細部を細かくピックアップしながらの解説は割愛し、コード全体の掲載に留めておきます。 今回のコードの全体は、以下の通りです：

ライセンス

このVCSSL/Vnanoコード（ 拡張子が「.vcssl」や「.vnano」のファイル ）は実質的な著作権フリー（パブリックドメイン) である CC0 の状態で公開しています※。 記事中にC言語/C++/Java言語などでのサンプルコードが掲載されいてる場合は、それらについても同様です。 そのままでのご利用はもちろん、改造や流用などもご自由に行ってください。

※ ただし、このコードの配布フォルダ内には、ダウンロード後すぐに実行できるように、 VCSSLの実行環境も同梱されており、そのライセンス文書は「 License 」フォルダ内に同梱されています （要約すると、商用・非商用問わず自由に使用できますが、使用の結果に対して開発元は一切の責任を負いません、といった具合の内容です）。 配布フォルダ内の各構成物の一覧やライセンスについては「 ReadMe_使用方法_必ずお読みください.txt 」をご参照ください。

※ Vnano の実行環境については、別途スクリプトエンジンのソースコードも一般公開しており、 何らかのソフトウェア内に組み込んでご利用いただく事も可能です。詳細はこちらをご参照ください。

この記事中の商標などについて

• OracleとJavaは、Oracle Corporation 及びその子会社、関連会社の米国及びその他の国における登録商標です。文中の社名、商品名等は各社の商標または登録商標である場合があります。
• Windows は、米国 Microsoft Corporation の米国およびその他の国における登録商標です。この記事は独立著作物であり、Microsoft Corporation と関連のある、もしくはスポンサーを受けるものではありません。
• Linux は、Linus Torvalds 氏の米国およびその他の国における商標または登録商標です。
• その他、文中に使用されている商標は、その商標を保持する各社の各国における商標または登録商標です。