For details, see How to Use.
Tool for Converting Units of Angles: Degrees and Radians
A GUI tool for converting the angle in degrees into radians, or radians into degrees. It also display the inputted angle graphically.
Sponsored Link
How to Use
Download and Extract
At first, click the "Download" button at the above of the title of this page by your PC (not smartphone). A ZIP file will be downloaded.
Then, please extract the ZIP file. On general environment (Windows®, major Linux distributions, etc.), you can extract the ZIP file by selecting "Extract All" and so on from right-clicking menu.
» If the extraction of the downloaded ZIP file is stopped with security warning messages...
Execute this Program
Next, open the extracted folder and execute this VCSSL program.
For Windows
Double-click the following batch file to execute:
For Linux, etc.
Execute "VCSSL.jar" on the command-line terminal as follows:
java -jar VCSSL.jar
» If the error message about non-availability of "java" command is output...
After the program has been launched
The following window will be displayed.
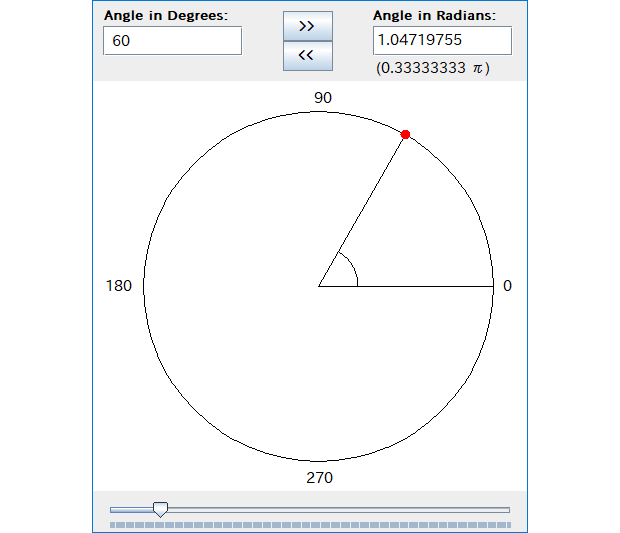
On the above window, you can perform the following conversions:
- How to convert the angle in degrees into the angle in radians
- To "Angle in Degrees" text field, input the value or expression of the angle in degrees, and click ">>" button to convert it. As the result, tha angle in radians will be set automatically to "Angle in Radians" text field.
- How to convert the angle in radians into the angle in degrees
- To "Angle in Radians" text field, input the value or expression of the angle in radians, and click "<<" button to convert it. As the result, tha angle in degrees will be set automatically to "Angle in Degrees" text field.
To "Angle in Degrees" or "Angle in Radians" text field, you can input expressions, instead of values.
For example, when you want to convert \( \frac{3}{2} \pi \) [rad] to the angle in degrees, input PI * 3 / 2 to "Angle in Radians" text fuekd, and click "<<" button. Then you get the result 120, as the angle in degrees.
Also, you can use various math functions, e.g.: sin, cos, tan, and so on. Note that, it is necessary to write arcsin(...) / arccos(...) / arctan(...) functions as asin(...) / acos(...) / atan(...). For example, when you want to compute the "degree" value of the angle of which the value of the tan(...) function is 1, input atan(1) to "Angle in Radians" text field.
Also, when you perform the above conversions, the inputted angle will be displayed on the window graphically (on "angle display" panel).
Theme
Degrees and Radians
As mentioned in the above How to Use section, there are two well-known units for measuring angles: "degree" and "radian".
Degree
A degree is a unit of angle, frequently used in practical purposes. For example, when you want to measure the angle of something in DIY, probably you use a protractor. On the protracter, various frequently-used angles are indicated in degrees (30-degree, 45-degree, and so on).
As you know well, 1-degree is 1/360 of the angle of one revolution:
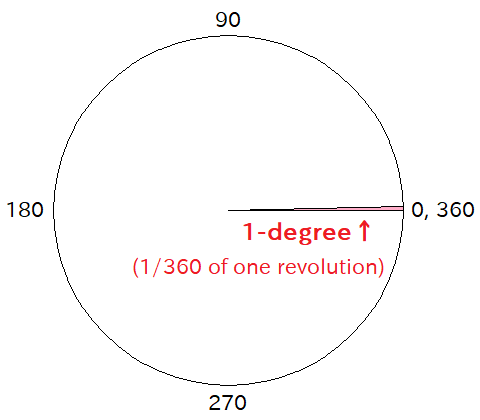
So the angle of the one revolution is 360-degree.
This number "360" is a special. It is very convenient for practical purpose, because 360 is divisible by 1, 2, 3, 4, 5, 6, (Oh my goodness! not divisible by 7), 8, 9, 10, ... and so on.
The above means that, we can express frequently used angles -- 1/2, 1/3, 1/4, 1/5, 1/6, ... of one revolution -- as simple numbers without using fractions, lile as 180-degree, 120-degree, 90-degree, 72-degree, 60-degree, and so on.
This property is very convenient for practical purposes (DIY and so on). Hence, when we measure angles in daily life, we mainly use the degree.
Radian
A radian is another unit of angle. As depicted in the following figure, when the length of the arc equals to the radius, the angle is 1 rad (where rad is the symbol of the unit of radian).
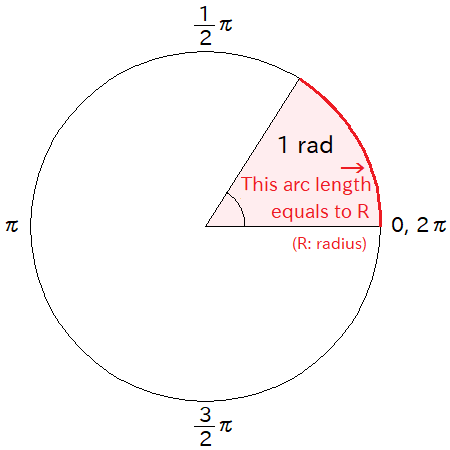
Hence, the angle of one revolution is \(2 \pi\) rad, which corresponds with 360-degree. You can convert an angle in degrees into the angle in radians, or radians into degrees, as follows:
\[ \rm{radians} = \frac{2 \pi}{360} \rm{degrees} \] \[ \rm{degrees} = \frac{360}{2 \pi} \rm{radians} \]The radian is frequently used in mathematical, theoretical, analytical fields.
For example, in such fields, "\(\sin\)" and "\(\cos\)" functions are defined as \(2 \pi\)-periodic functions, not 360-periodic functions.
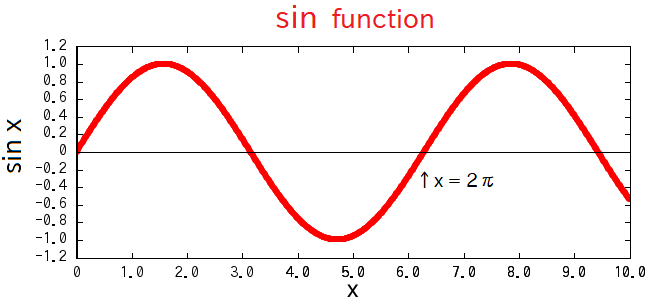
So when we regard that the parameter \(x\) of \(\sin x\) represents an angle, we must use the radian as the unit -- "\(2 \pi\) corresponds to one revolution".
Why are the \(\sin\) and \(\cos\) functions defined as \(2 \pi\)-periodic, not 360-periodic?
Probably there are many reasons and we don't know all of them, but one of great advantages is that:
We can get the polynomial representations (see: Taylor series)
of \(\sin\) and \(\cos\) functions in the most simple form, when they are \(2 \pi\)-periodic:
What beautiful polynomial expressions!
Surprisingly, the above polynomial expressions don't contain \(\pi\) anywhere, but they express \(2 \pi\)-pediodic \(\sin\) and \(\cos\) functions. The above expressions are important in theoretical and analytical fields, so we don't want to break the above most simple form, by scaling the parameter \(x\).
Hence, the period of the \(\sin\) and \(\cos\) functions should be \(2 \pi\) in theoretical and analytical fields, and then it is natural to use the radian as the unit of angle.
A digression: Relationship between sin and cos functions and exponential function
Similar to above, we can get the polynomial representations of exponential functions: \(a^x\). It takes the most simple form when \(a = e\), where \(e\) is Euler's number (2.7182818...):
\[ e^x = x^0 + x^1 + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + ... = \sum_{n=0}^{\infty} \frac{x^n}{n!} \]Fuethermore, extend the parameter \(x\) from a real number to a complex number, and replace the \(x\) in the above to \(i x\) (where \(i\) is the imaginary unit), then \(e^{i x}\), \(\sin x\), and \(\cos x\) functions are liked as:
\[ e^{i x} = \cos x + i \sin x \]What beautiful equation! Isn't it?
The above equation is very important, and we can express it in the most simple form by using \(e\) and \(2 \pi\), as we we have seen.
At one glance, the numbers \(e\) and \(\pi\) seem not to be simple at all, so you probably wonder why people use them frequently in theoretical fields. However, as we have seen, they make mathematical/theoretical concepts simple and beautiful. So, don't you feel that the radian is beautiful?
Code
About language
This program is written in VCSSL.
VCSSL is a scripting language having C-like simple syntax. So, if you are accustomed with C-like languages (C, C++, and so on), you can read code of this program easily.
Whole Code
All code of this program is written in the text file "RadianConverter.vcssl". You can open by your favorite text editor, and modify freely. It does not require to be compiled for running.
The following is the whole code of this program:
As the above, the code of this program has about 300 lines.
For details, see comments in the code.
License
The license of this VCSSL / Vnano code (the file with the extension ".vcssl" / ".vnano") is CC0 (Public Domain), so you can customize / divert / redistribute this VCSSL code freely.
Also, if example code written in C/C++/Java are displayed/distributed on Code section of this page, they also are distributed under CC0, unless otherwise noted.
|
Tool For Converting Units of Angles: Degrees and Radians |
|
|
|
A GUI tool for converting the angle in degrees into radians, or radians into degrees. |
|
Fizz Buzz Program |
|
|
|
A program printing the correct result of Fizz Buzz game. |
|
Vnano | Output Data of Numerical Integration For Plotting Graph |
|
|
|
Example code computing integrated values numerically, and output data for plotting the integrated functions into graphs. |
|
Vnano | Compute Integral Value Numerically |
|
|
|
Example code computing integral values numerically by using rectangular method, trapezoidal method, and Simpson's rule. |