今回は最終回として、少し応用的な内容を扱ってみます。 具体的には、CSVファイルに数値データを読み書きして、それをグラフソフトウェアに読み込ませ、2次元/3次元のグラフを描画してみます。
これまでは、式や変数をはじめ、条件分岐や繰り返し、ファイルの読み書きなど、 プログラムにおける基本的な処理について説明してきました。 でも、前回までで基本はだいたい出そろいました。 これまでの内容を組み合わせれば、もう色々な事ができるはずです。 そこで最終回となる今回は、より実践的な内容に挑戦してみましょう。
これまでに扱ってきたのは、いわば「 プログラムの書き方を学ぶためのプログラム 」でした。 画面に表示する内容や、ファイルに書き込む内容なども、プログラムの動作を確認するためのものばかりでした。 変数の値や入力値などについてもそうで、いわば「 とりあえずの値 」を入れていましたね。
でも、実際のプログラムは、もっと具体的な目的があって使われるものです。 読み込んだり書き込んだりする内容も、ちゃんと意味や使い道があるものになるでしょう。 たとえば、なにか別のソフトで使うためのデータを作成したり、 逆に別のソフトで作ったデータを読み込んで処理したり、といったパターンはよくあります。
別のソフトやプログラムとデータをやり取りする方法はいくつかありますが、 単純にファイルの読み書きで行うのも、一般によく使われる方法です。 たとえばプログラムからデータをファイルに書き込んで、そのファイルを別のソフトで開くわけです。 人間同士が、手紙やメールでやり取りする感じに似ていますね。
このようにファイル経由で別のソフトとやり取りする場合、 「 ファイル内に、データをどういう書き方で書くか 」というルール を決めておく必要があります。 これが書く側と読む側でちぐはぐだと、データを正しく伝えられません。
さて、「 ファイルの読み書き 」の回 では、 以下の2通りの書き方を使いました：
(1) は究極的にシンプルですが、値の個数が多い場合にファイルだらけになって管理が大変です。 その点で (2) のほうが実用的でしょう。でも、もう一歩すすんで、1行に複数の値を書けると、さらに便利です。 そこで実際には、
のような書き方がよく使われます。 こうすると、たとえば以下のような「 表 」の形のデータを書くのに便利です：
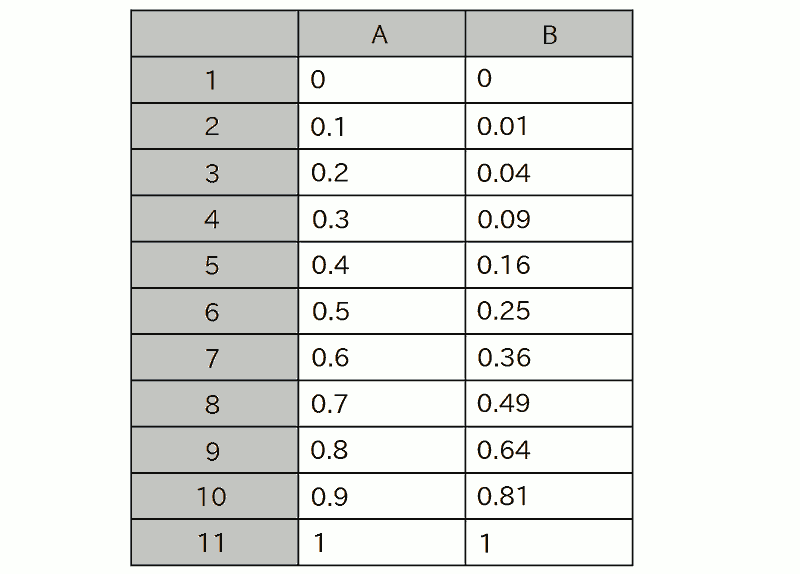
このような表の形のデータは、よく表計算ソフトなどで登場します。 実際に表計算ソフトで上の図のデータを打ち込み、 「 CSV 」という形式で保存（「 エクスポート 」メニューなどから ）すると、以下のようなファイルが作られます：
[ 表計算ソフトで保存したファイル「 hyou.csv（ ひょう.csv ）」の中身 ]
（ ※ CSVファイルをふつうにダブルクリックすると、表計算ソフトで開かれてしまう事が多いでしょう。 その場合はファイルを右クリックし、「 プログラムから開く 」メニューからテキストエディタ（ メモ帳など ）を選択して開いてください。 ）
「 , 」記号はコンマやカンマと呼ぶので、このようなファイルの書き方は、「 カンマ区切りの値 」を意味する英語 「 Comma Separated Values 」を略して「 CSV（ シーエスブイ ） 」形式と呼ばれています。 そしてCSV形式で書かれたファイルはCSVファイルと呼ばれます。 CSVファイルは、いろいろなソフトで幅広くサポートされているため、プログラムでも読み書きする場面がよくあります。 よって、今回もCSV形式を用いる事にしましょう。
さて、CSVファイルを使って何をするかですが、今回は絵的にわかりやすい 「 グラフを描く 」という事を行ってみましょう。 グラフを描くソフトは、CSVファイルを使う典型的なソフトの一つです。 高機能なものもありますが、今回はシンプルな「 1 行ごとに 1 つの点を描いてくれるタイプのグラフソフト 」を用意します。 たとえば：
などがあります。これらはPC用の各種OSで動作し、無料で使用できます。
試しにリニアングラフ2D（ ※ 3Dではない ）を使って、 先ほどのCSVファイルからグラフを描いてみましょう。 まず上のリンクからソフトをダウンロード・展開し、 中の「 RinearnGraph2D.jar（JARファイル）」をダブルクリックして起動してください。
そしてメニューバーの「 File（ファイル）」メニューから「 Open File（ファイルを開く）」を選び、 先ほど表計算ソフトで保存したCSVファイル「 hyou.csv 」を読み込んでプロットしてください。
（ ※ 表計算ソフトが無い場合などは、上で掲載してある「 hyou.csv 」の内容をテキストエディタ（ メモ帳など ）で書いて保存してください。 保存の際は、「 ファイルの種類 」の項目を「 すべてのファイル 」にしてください。）
実際にプロットした様子は下図の通りです：
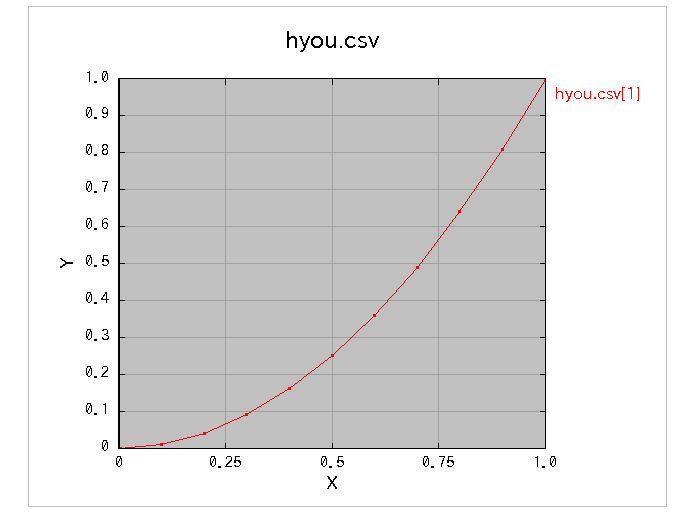
このように画面上に、いくつかの点が線でつながれたグラフが表示されます。 この中の 1 つの点が、ファイル内の 1 行に対応していて、左の列（「 , 」記号の左側 ）の値を x 座標、右の列の値を y 座標とみなした位置に描かれています。 実は、さっきのCSVファイルにおいて、右の列の値は、左の列の値を 2 乗したものになっていました。 よってこのグラフは、中学校で習う「 y = x2 」のグラフになっています。 きれいな形ですね。
ところで、上で使ってみたリニアングラフは、実はVCSSLと同じ開発元のソフトです。 なので、VCSSLには標準で、プログラム内からグラフソフト（ ※ リニアングラフが使われます ）を起動させたり、操作したりする機能がサポートされています：
最初の行「 import 〜 」は、グラフソフトを操作するために必要な「 ライブラリ 」というものを読み込んでいる行です。 ライブラリとは、プログラム内で使う機能を増やすためのものです。 この行により、グラフ関連の関数が使えるようになります。
続いて使っている 「 newGraph2D （ニューグラフ・ツーディー）」関数は、 グラフソフトを起動する関数です。その際、グラフが複数あっても区別できるよう、ID番号が割りふられます。それを「 = 」の左の変数「 graphID 」に代入しています。
最後の「 setGraph2DFile（セットグラフ・ツーディー・ファイル）」関数は、 グラフソフトにCSVファイルなどを読み込ませてくれる関数です。 カッコ内の最初にグラフソフトのID番号を指定し、その次に、読み込ませるファイルの名前を書きます。
このプログラムを、先ほどのCSVファイル「 hyou.csv 」と同じフォルダ内に置いて実行すると、グラフが表示されます：
このように、結果は手動でグラフソフトを使った場合と同じです。 ある意味、手動でプロットしたほうが「 プログラムを別のソフトと連携させてる感 」が出るかもしれないですが、 せっかくなので、今回は上のようにプログラム内からグラフソフトを起動し、CSVファイルを読ませる事にしましょう。 もちろん、なにか別のグラフソフトを使いたい場合など、あえて手動でグラフ表示を行っても OK です。
さて、CSVファイルとグラフソフトがどんなものか大体わかったところで、本題です。 プログラムでデータをCSVファイルに書きだして、そのデータをグラフソフトに描画してもらいましょう。 これは、自作のプログラムを、別のソフトやプログラムと組み合わせて使う、いい例になります。
CSVファイルを読み書きするには、まず書き込む内容に「 , 」を付けたり、 読み込んだ行を「 , 」で区切ったりする処理が必要になりますね。 また、実際のCSVファイルにはいろいろな書き方があり、 値が「 " 」で囲まれていたりして、もっと複雑な処理が必要になる事もあります。
もちろん、そういった処理を自力でプログラムに書く事もできるのですが、 VCSSLにはCSVファイルを手軽に読み書きするための機能が、標準で用意されています。 今回はそれを使いましょう。 一番単純なのは、ファイルを開く open 関数で、CSV読み書き用のモードを使う事です。 たとえば書き込みなら、以下のようにします：
このように、open 関数の中で「 WRITE_CSV（ライト・シーエスブイ） 」と書いていますが、 これはファイルにCSV形式でデータを書き込むためのモードです（ 実はここは "wcsv" と書いても同様に動きます ）。 このモードを使った場合、上のように write 関数のカッコ内に複数の値を書くと、それらは「 , 」記号で区切ってファイルに書き込まれる ようになります。
上のプログラムでは、for 文を使う事で、ファイルの各行を自動で書き込むようにしています。 for 文の詳細は「 くりかえし処理 」の回を読みかえしてみてください。 ここでは、カウンタ変数「 i 」の値が 0 からスタートし、1 ずつ増えながら、10 までの間ずっと { ... } の中の処理がくりかえされます。 その中で毎回 x と y の値を求め、writeln 関数でファイルに 1 行書き込んでいます。
このプログラムを実行すると、 「 file.csv 」という名前のCSVファイルが作られ、その中に x と y の値が書き込まれます。 そして、それがグラフソフトに読み込まれて、以下のようなグラフが表示されます：
また先ほどと同じグラフですね。 それもそのはず、上のプログラムで求めている x は、 for 文のカウンタ変数 i に 0.1 をかけたものなので、 0 から 1 まで 0.1 ずつ変化します。 y はその2乗としています。 これらは先ほど表計算ソフトで作った「 hyou.csv 」と同じなので、同じグラフになったわけです。
実際にプログラムで書き込んだCSVファイル「 file.csv 」の中身を見てみましょう：
このように、たしかに x の値（ 「 , 」の左の列 ）は 0.1 ずつ増えていて、y の値（ 左の列 ）は x の 2乗になっています。 ちゃんと計算して書き込めているようです。
でも上の内容には、たとえば「 0.010000000000000002 」のように、 いくつかの値に小さなゴミのようなものが付いています。 これは 「 式と計算 」の回 で説明した、小数（ 浮動小数点数 ）の誤差によるものです。 この誤差は非常に小さいので、ふつうはほとんど問題にならないですが、このようにファイルに書き出すとじゃまになる事もあります。 その場合、書き込み前に round 関数で適当な桁数に丸めれば、きれいになります ：
この例では x と y の値を、小数点以下が5ケタまでになるよう四捨五入しています。 「 HALF_UP（ハーフアップ） 」のかわりに「 HALF_UP_SIGNIF（ハーフアップ・シグニフィカンド） 」と書けば、 有効数字のケタ数指定もできます。 さて結果は：
誤差が丸め込まれて、きれいになりましたね。 「 00...0 」と続くケタは省略されてしまっていますが、 ちゃんと内部で小数点以下5ケタまでに丸められています。
続いて、CSVファイルからデータを読み込んでみましょう。 これも、別のソフトで作ったデータを、プログラムで加工したい場合などによくあるパターンです。 ファイルを開く open 関数には、CSV形式の読み込みのためのモードが用意されています：
基本的には、「 ファイルの読み書き 」の回で説明した、ループを使った読み込み と同様です。 ファイルを開いた後に countln 関数で行数を数えて、 for 文 でくりかえし1行ずつ、readln 関数を使って読み込んでいます。
違う点は、まず open 関数のカッコ内で 「 READ_CSV （ リード・シーエスブイ ) 」 と書いている事です。 これはCSV形式のファイルを読み込むためのモードで、書き込みで使っていた「 WRITE_CSV 」の逆バージョンです。
このモードでは、readln 関数が、読み込んだ行の内容を「 , 」記号で区切ってくれるようになります。 その結果は、「 = 」記号の左にある配列（ ここでは「 line 」 ）に代入されます。 その配列の [ 0 ] 番には一番左の列の値が入り、[ 1 ] 番にはその右の列、[ 2 ] 番には（ あれば ）さらにその右の列 ... という順番で値が入ります。
読み込んだ値をその場で println 関数で表示してもよいのですが、それでは実用的な例になりませんね。 実際には、読み込んだデータにいろいろな処理を加える事が多いでしょう。 そこで、ここではあらかじめ宣言しておいた x と y の配列に、各行ごとの値を入れておく処理にしています。 それを、あとでまとめてで表示しています。
実行結果は以下の通りです：
この通り、ちゃんとCSVファイルの値を正しく読み込めている事がわかりますね。
（ ※ println 関数のカッコ内に複数の値を書いた場合、このように空白（ タブ ）で区切って表示されます。 ）
プログラム内でのCSVファイルとグラフソフトの扱いにもなれてきたところで、 一歩進んで、3Dのグラフを描いてみましょう。 まずは、これまでの2Dグラフの延長線上で簡単に描ける、「 線グラフ 」からです。 この場合、CSVファイルを 3 列にして、各行に「 x,y,z 」のように点の座標を書けば OK です：
ちょっと長いですが、基本的には先ほどの2Dグラフの場合とほぼ同じです。 違うのは、ところどころ「 Graph2D 」のかわりに「 Graph3D 」になっている事と、 z の値の処理が追加されている事くらいです。 z の値は x の3乗にして、writeln 関数で y の右の列に書き込むようにしています。 このプログラムを実行すると：
このように、CSVファイル「 file.csv 」に「 , 」区切りで3列のデータが書き込まれます。 一番右の列に z の値が書かれています。たしかに x の値（ 一番左の列 ）の3乗ですね。 続いて、以下のような3Dグラフが描画されます。ちゃんと立体的に曲がった曲線になっていますね。
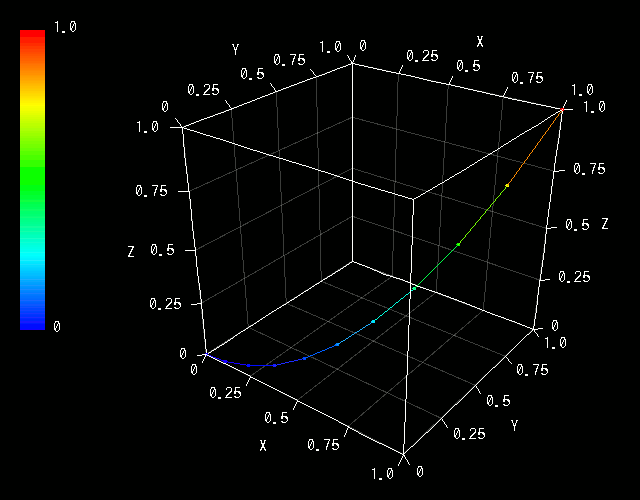
さて、最後です。少しむずかしくなってしまいますが、3Dのメッシュグラフを描いてみましょう。 メッシュグラフというのは、SF映画などであみの目のように立体形状が描かれている、あれです。 3Dグラフと言えば、やはりあれでしょう！
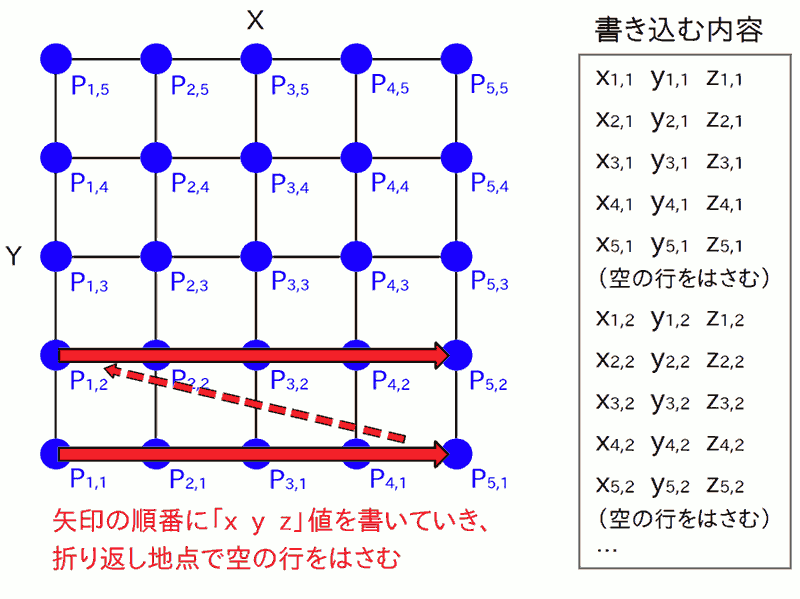
メッシュグラフを描くためには、CSVファイルに、独特の書き方でデータを書き込む必要があります。 1 行につき 1 点の座標を「 x,y,z 」と書く事は同じですが、その点を書いていく順番が決まっています。 たとえば、メッシュ上の点（ 格子点 ）が、X-Y 平面において下図のように並んでいるものとしましょう：
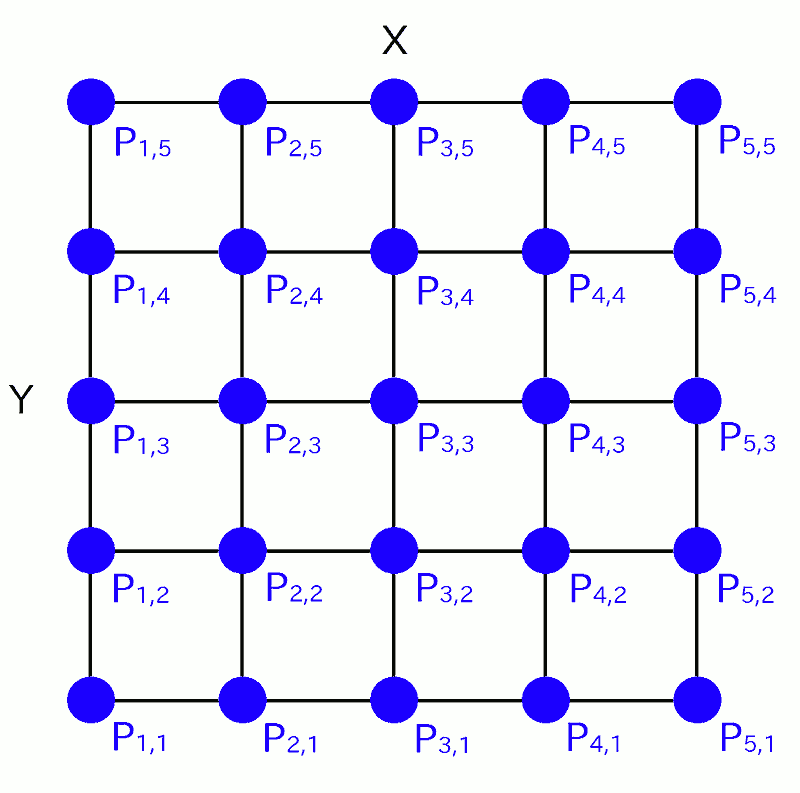
（ ※ もちろん、それぞれの点は z の値も持っていますが、それはこの図では画面と垂直な方向です。）
さて、この図のような場合、まず y は端（ はし ）の値に固定して、x 軸の方向に点の座標を書いていきます。 この図では P1,1 から P5,1 までです。 そして x 軸の端まできたら、空（ から ）の行を 1 行だけ書き込みます。 続いて、y 軸方向に 1 個だけ進んで、また x 軸の方向に点の座標を書いていきます。 この図では P1,2 から P5,2 までです。 その後はまた空の行を 1 行だけはさんで、P1.3 から P5.3 まで書きます。 これを繰り返して、最終的に P5,5 まで書き込めば終わりです。
なんだかややこしい書き方ですね。でも実は、プログラムだと意外と簡単なのです：
このように、基本的には for 文が2重になった事と、y の値の計算式が少し違うだけですね。 内側にある（ 上から 2 つめの ）for 文は、これまでと同様に、x の値を 0.1 ずつ増やすくりかえしです。 いまの場合は、これは先ほどの例の P1,1 から P5,1 までのように、 書き込む点をx 方向に動かしていく事に対応しています。 x が端（ はし ）にくると、この for 文は一旦終わりです。
すると、外側にある（ 上から 1 つめの ）for 文が 1 周回りますね。 これによって、カウンタ変数 j の値に 1 が足されて、y の値が 0.1 だけ増えます。 そして再び内側の for 文がくりかえされ、先ほどの例の P1,2 から P5,2 までのように、 書き込む点が x 方向に動いていきます。後も同様です。確かに先ほどの例の通りになりますね。
さて、上のプログラムでは、z については少し複雑に 「 z = y2 - x2 + x 」 という値にしています。 グラフがどんな形になるのか、ぱっとイメージするのはちょっと難しいですね。 でも、実はそれが狙いです。 結果が簡単にイメージできないからこそ、プログラムを書いてコンピューターに計算させる意味があると思いませんか？
それでは実行してみましょう。実行すると、まず以下の内容がCSVファイル「 file.csv 」に書き込まれます：
ちゃんと想定通りの内容ですね。そして、以下のようなグラフが表示されます：
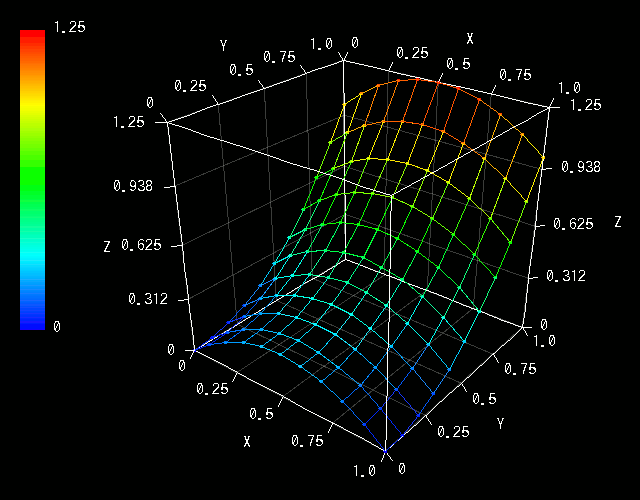この通りです。思いもよらない形だったのではないでしょうか？ という事は、
いま私たちはコンピューターに「 答えを教えてもらった 」わけです。
このコーナーでのこれまでのプログラムは、結果がわかりきったものばかりでしたが、今回は違います。
「 難しいグラフの形を求める 」という、れっきとした問題を、コンピューターとプログラミングによって解いたわけです！
さて、もしかすると上のグラフの形が、予想どおりだったという人もいるかもしれません。 そこで最後におまけとして、もっと複雑なグラフを描いておしまいにしましょう。 内容が数学的で少し難しくなってしまうため、詳しい説明は省略し、プログラムとグラフだけ掲載します：
このプログラムで描かれるのは、 座標の原点との距離を r 、X軸とのなす角度を θ として、「 z = sin(5θ+10r) sin(6r) 」のグラフです。 ちなみに、このような r と θ による表し方を「 極座標 」といいます。さあ、実行してみましょう：
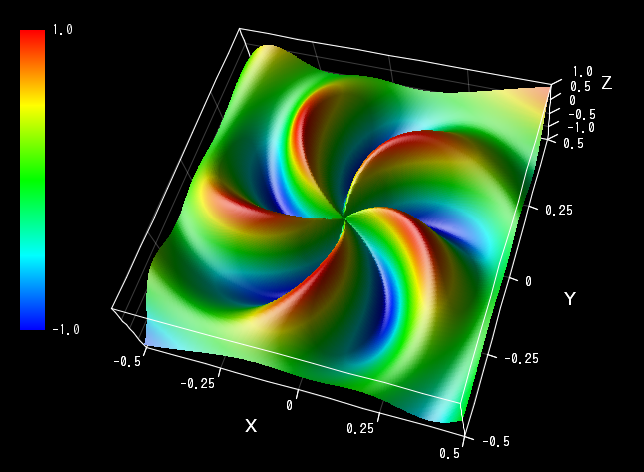（ ※ グラフの「 Option（オプション）」メニューから「 Tesselation（曲面高画質化）」を選択すると綺麗になります。）
三角関数が入り混じった複雑な式からすると、意外なほどきれいなグラフですね！ さらに、z の値を計算している行を、以下のように 1 行だけ書き換えると、もっと複雑なグラフになります：
実行結果は以下の通りです。 このグラフをすぐに、そして正確に手で描けるという人は、ほぼいないのではないでしょうか。
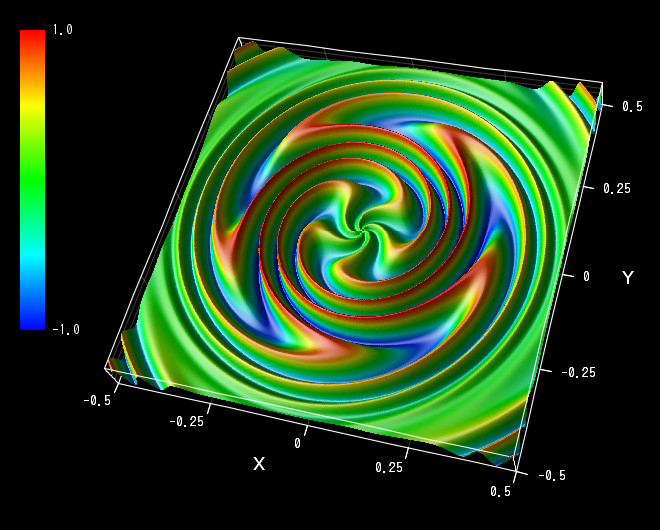
コンピューターは、言われた事を忠実に行うだけのやや不器用な存在ですが、 そのかわり処理の正確さとスピードは、人間よりもはるかに優れています。 そんなコンピューターの長所を理解して活用すると、上のグラフのように、人間だけでは見えなかった新しい世界を見せてくれます。 それでは、楽しいプログラミング生活を！
（ VCSSLスタートアップガイドは、この回で最終回です。 ）