
前回の途中で、式というものが登場しました。 プログラムの中で式を書くと、コンピューターが自動でその値を計算してくれるのでしたね。 今回は、色々な式を書いて計算してみましょう。
本来ならば、まず「 式とは何か? 」という詳しい説明が必要かもしれませんが、 実はそれは少し難しい文法規則の話になってしまうため、ここではやめましょう。 ここ言う「 式 」とは、あまり深く考えず、要するに普通の言葉で言う「 数式 」や「 計算式 」といった程度の意味と思っておきましょう。
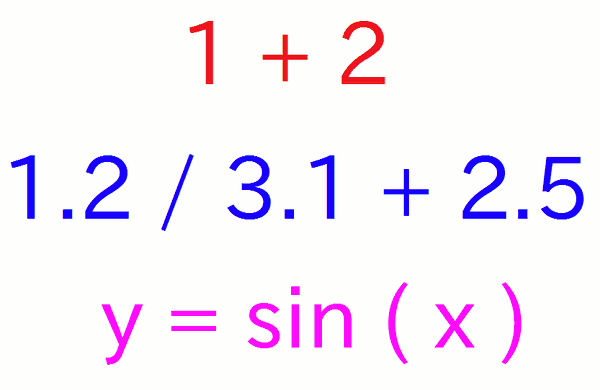
さて、プログラムの中に式を書くにはどうすればよいでしょうか。 今までの話の流れからすると、「 この行は式です 」と知らせるキーワードなどが必要と思うかもしれません。 しかし式に関しては、そういったものは不要です。 プログラムの中身は、式が大半を占めるからです。
プログラミングを始めたての頃は、プログラムの中の各行が、何をする行なのかを判断するのが大変です。 実際、後の回で登場する「 制御文 」など、プログラム内には式以外のものもあります。 しかし、それらは先頭のキーワードなどから判断できるようになっています。 なので、『 そういった「 式でないもの 」以外は式だ 』 と思ってしまうのが手っ取り早いでしょう。
では、実際に式を計算するプログラムを書いてみましょう:
これだけで OK です。 簡単ですね。でもこのプログラムを実行しても、画面には何も表示されません。 確かに 12345 + 67890 の値は計算されるのですが、その結果を画面に表示させる処理を書いていないからです。 そこで前回のように print 関数を使いましょう:
この print 関数は、カッコの中身を画面に表示させる機能を持っている のでしたね。 実際に上のプログラムを実行すると、以下の通り、12345 + 67890 の計算結果が表示されます:
上の例のように、式は関数のカッコ内など、いろいろなところに結構自由に書けます。 「 式はここに書かないといけない 」 というよりは、むしろ逆に「 式を書けないところもいくつかある 」 くらいのイメージで、気軽にとらえておきましょう。
上で書いたプログラムには、右端に「 ; 」 記号が付いていますが、 これは前回説明した通り、一つの処理の終わりを意味するものでしたね。 いちいち付けるのは面倒ですが、その代わり、とにかくこの記号の位置までは一つの処理なので、改行しても別の処理にはなりません。 なので以下のように、式の途中で自由に改行したり、空白をはさんだりしても大丈夫です:
上のプログラムを実行すると、以下のようにちゃんと計算結果が表示されます:
式の長さに制限はなく、何文字でも、何行になっても大丈夫です。
ここまでは足し算を行ってきましたが、もちろん引き算もできます:
この計算結果はマイナスになるはずですが、それでも大丈夫です。 実際に上のプログラムを実行してみると、以下のようにちゃんとマイナスの値が表示されます:
かけ算や割り算もできますが、私たちが普段使っている「 × 」記号や「 ÷ 」記号は、キーボードにはありません。 そこで代わりに、かけ算には「 * 」記号( アスタリスクと呼びます )を使い、 割り算には「 / 」記号( スラッシュと呼びます )を使います。 実際に使ってみましょう:
上のプログラムで使っている println 関数は print 関数とほぼ同じですが、画面にカッコ内の値を表示した後に改行してくれます。 そのため、複数の式の値を表示したいときに、行ごとに区切られて読みやすくなります。 実行結果は以下の通りです:
ちゃんと 2 * 3 の値である 6 と、10 / 5 の値である 2 が、行ごとに表示されていますね。
さて、ここで計算に使ってきた「 + - * / 」のような記号の事を、正確には 「 算術演算子 」 と呼びます。 難しそうな呼び方ですが、怖がる必要はありません。要するに、ただの計算の記号以上の何者でもありません。 算術演算子をまとめると、以下のようになります:

以下のプログラムのように、式の中に複数の計算が含まれている場合もあります:
このような場合、「 どのような順序で計算されるか 」によって、結果が異なります。 たとえば、まず 1 + 2 を計算して、その値に 3 をかけた場合、計算結果は「 9 」になります。 逆に、まず 2 * 3 を計算して、それに 1 を足した場合、計算結果は「 7 」になります。 実際には:
この通り、後者のように計算されます。 これは、私たちが小学校で習うのと同じように、 「 かけ算・割り算は、足し算・引き算よりも先に計算する 」というルールがあるからです。 これをもう少しプログラミングの世界の言葉で言うと、 『 「 * 」と「 / 」演算子は、「 + 」と「 - 」演算子よりも優先度が高い 』 などと言います。 優先度が高い演算子のほうが、先に計算されるのです。

そして、かけ算と割り算などのように、 同じ優先度の演算子が並んでいるときは、左から順番に計算されます:
上のプログラムを計算すると、左から順にまず 4 * 5 が計算されて 20 になり、続いてその値が 10 で割られて、最終的に 2 になります。 実際の実行結果は以下の通りです:
たとえば「 長さの合計を2倍したい 」というように、 かけ算よりも足し算を先に行ってほしい場合もありますね。 そのような場合は、先に計算してほしい部分をカッコで囲めばOKです:
上のプログラムを実行すると、まずカッコ内の 30 + 50 + 80 が計算されて 160 になり、それに 2 がかけられて 320 になります。 実際の計算結果は以下の通りです:
カッコは何個でも使う事ができ、入れ子にする( 重ねる )事もできます。
ところで、以下のように、小数点のある数の計算を行う事もできます:
上のプログラムの実行結果は以下の通りです:
ちゃんと結果にも小数点が付いています。 上のように小数点のある数を、ここでは「 小数 」と呼ぶ事にしましょう。 より厳密に「 浮動小数点数 」や「 実数 」と呼ぶべきだ、という意見があるかもしれませんが、 どちらも少し難しそうなイメージが出てしまうため、ここでは細かい厳密さは置いておく事にします。
なお、「 1 」や「 2 」のように、小数点の付いていない数は「 整数 」と呼びます。
さて、ここでとても重要なルールがあります。 それは 「 プログラム内の整数と小数は、別の種類のデータとして扱われる 」 という事です。
といっても、この事自体は、そう驚く事ではありません。 なぜなら、私たち人間だって、手計算で筆算をする場合などには、整数と小数では計算のやり方が少し違うので、両者を区別して適切な計算方法を使い分けているはずです。 全般的に、整数同士の筆算よりも、小数同士の筆算の方が少し複雑になるので、小学校でもまず前者を習ってから、後で後者を習いましたね。 ただ、そういった計算方法の切り替えは、小学校で毎日たくさん訓練したので、もうあたりまえすぎて、普段は意識せず行っているかもしれません。でも、区別はしているはずです。
これはコンピューターの電子回路にとっても同じで、やはり小数と整数では計算のやり方が違うので、 「小数のデータ」と「整数のデータ」は、内部で区別して扱う必要があるのです。 また、私たちが小数を書き表すためには、整数では不要な「 小数点 」というものを付ける必要がありますね。 それと同様に、やはりコンピューター内部で(1と0の列として)小数のデータを表す際にも、整数にはない工夫が必要になってきます※。
( ※ 詳しくは、IEEE754という規格で決まっています。 )
このようにコンピューターの気持ちになって考えれば、 プログラム内で小数と整数を別の種類のデータとして扱うのは、不思議な事ではありませんね。 このような種類の事を一般に「 データ型 」、 または単に「 型 」( 英語では「 タイプ 」)と呼びます。整数と小数は型が違うというわけです。
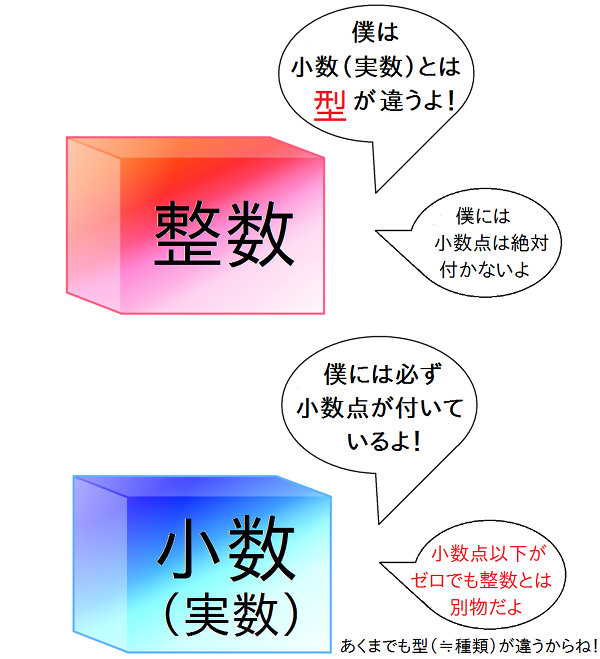
ただし、 プログラム中に直接書かれた数値が整数か小数かは、小数点以下がゼロかどうかではなく、単純に小数点が付いるかどうかだけで判断される という事に注意が必要です。つまり 「 1 」と「 1.0 」は、前者が整数型のデータで、後者が小数型のデータであり、別のもの と見なされます。
整数と小数の違いに特に気を付ける必要があるのは、割り算を行うときです。 実は 整数と小数とで、割り算の振る舞いや結果が違うからです。 一体どう違うのでしょうか?
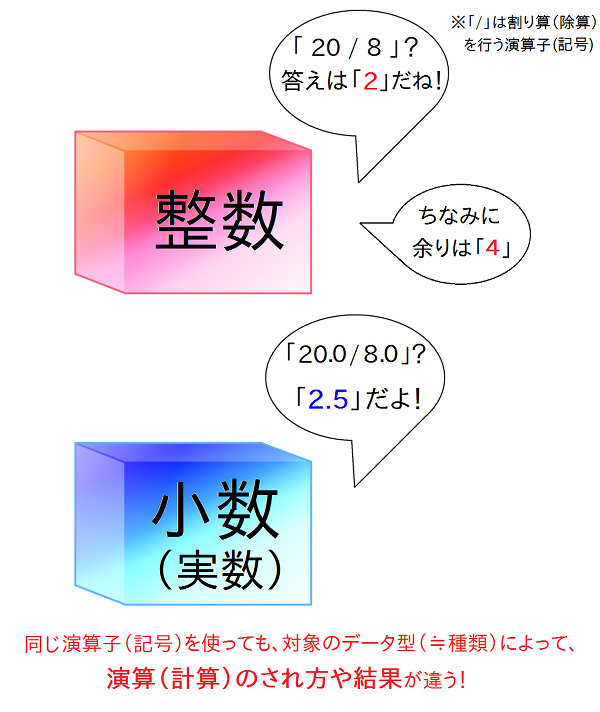
例として 「 20 / 8 」について考えてみましょう。 多くの人は、この式の答えは 「 2.5 」だと思うでしょうし、それは確かに一つの正解です。 でも、小学校時代に、小数を習う前には、どう答えたでしょうか? 「 2 余り 4 」 と答えたのではないでしょうか。懐かしいですね。 これも一つの正解でしょう。つまり割り算には、そもそも整数と小数で2種類の答え方があるわけです。
そしてプログラム内で、整数同士で割り算を行うと、後者のように整数の答えが求まります。 余りは「 % 」という演算子で計算すれば求まります:
上のプログラムの実行結果は以下の通りです:
ちゃんと「 2 余り 4 」という答えが求まっていますね。
一方、小数同士で割り算を行った場合は、小数の答えが求まります。 とにかく数値に小数点を付ければ、小数と見なされるのでしたね。試してみましょう;
上のプログラムの実行結果は以下の通りです:
今度は「 2.5 」という答えが求まりました。慣れるまでは、両者の違いに注意が必要です。
では、整数同士でもなく小数同士でもなく、以下のように整数と小数を両方使った割り算の結果は、どちらの型になるのでしょうか?
結果は以下の通りです:
小数の結果が得られましたね。 実は、割り算だけでなく、かけ算や足し算・引き算も含めて、算術演算子の計算結果の型は、以下のルールで決まります:
( ※ より厳密には、整数と小数を組み合わせた計算の場合、整数のほうの値が小数に変換されてから、小数同士の計算が行われます。)
割り算以外にも、整数と小数の扱われ方の違いには、注意が必要な点があります。 それは小数における「 誤差 」です。
より詳しく言うと、「 コンピューター内で保持している小数の値や計算結果が、正確な値からずれてしまう 」事に注意が必要なのです。 そんな事が起こったら大変じゃないか? そう、知らないと結構大変なのです。 論より証拠、まずは以下のように計算させてみましょう:
正しい値は 0.3 のはずですね。しかし実行結果は:
と、このように正しい値(0.3)から 0.00000000000000004 だけ大きな値になっています。 整数で計算していた時は、こんな奇妙な事は起こりませんでしたね ※。 でも、小数ではよくある事なので、要注意なのです。
(※ 整数でも、値が極端に大きくなったりして、扱える範囲を超えてしまうと、変な値になる「オーバーフロー」という現象が生じる事はあります。しかしそれは、値の範囲さえ注意すれば防げます。)
もう一つ例として:
と計算させると:
今度は正しい値(0.9)から 0.00000000000000001 だけ小さな値になってしまいました。 どちらの場合にも、正しい値からほんの少しだけずれています。このずれが、誤差です。
このような誤差が生じる理由をちゃんと説明しようとすると、 土台となる長い説明がいくつも必要なのですが、 一言で言うと、これはコンピューター内部での、小数の扱い方の都合によって生じてしまうものです。 もっと詳しく知りたい方は、「 浮動小数点数 誤差 」などとWeb検索すると、色々なページで解説されています。 でも、誤差が生じる理由は複数あって、それぞれが結構難しいです。
しかし何よりも重要なのは、このような誤差の存在を事を知った上で、どう対処するかという事です。 という事で、一番単純な方法で対処してみましょう。
幸い、この種の誤差は、もとの値と比べてかなり小さいという特徴があります。 そして多くの用途においては、上の例のように小数点以下17桁目とかにくる値は、もう無視して捨ててしまってもいいと思いませんか? 私たちが日常で小数の計算をする場合も、値が割り切れなかったりすると、「 小数点以下5桁もあれば十分だろう 」などと計算を打ち切ったりしますね。 プログラムでもそうしてみましょう。
ただ、単純に「 小数点以下5桁よりも小さい桁は捨てる 」とすると、 0.30000000000000004 は 0.3 になって OK ですが、0.8999999999999999 は 0.89999 になるはずで、あまりうれしくありません。 後者は 0.9 になってほしいですね。 なので、実際には単純な切り捨てよりも、小学校で習った「 四捨五入 」などの工夫した方法で、余分な桁を落とす場合が多いです。 このような、数値の余分な部分を落とす処理の事を、 「 丸め(まるめ)」 や 「 端数(はすう)処理 」 などと呼びます。
それでは実際に、先ほどの計算結果を、四捨五入で小数点以下5桁に「 丸め 」て表示させてみましょう:
実行すると:
無事、誤差の部分が「 丸め 」られて落ちましたね。 このように、値や式を round(ラウンド)関数で囲むと、 少数の値の中で、使いたい桁数よりも小さな部分(端数)を丸める事ができます。
なお、上のプログラム内で、「 5, HALF_UP (ハーフアップ) 」の部分が、「 小数点以下 5 桁より小さい部分を四捨五入 」という指示になります。
小数の誤差は、上のように丸めてしまえば済む場面が多いのですが、誤差や精度がとても重要な用途では、 別の方法で対処される事もあります。
例えば、プログラミング言語によって呼び方は異なるのですが、十進型などと呼ばれる少し特別なデータ型を使って、小数の計算を行う方法などがあります。 その方法では、上で見てきたような種類の誤差は生じません。
もう一つ、ものすごく長い桁数の小数を扱いたい場合には、別の特殊な方法が用いられる事があります。 ふつうの小数のデータ型は、扱える桁数が(たかだか十数桁くらいに)限られていて、扱いきれない部分は勝手に丸められて、そこで誤差が生じます。 それでも数百桁、数千桁といった桁数を正確に扱いたい場合は、多倍長計算という特別な方法が使用されます。
ただ、誤差には色々な種類があって、「 どれか最強の方法を使えば、すべての誤差を気にする必要が無くなる 」というわけではないので、注意は必要です。 むしろ逆に、そのような厳密さが要求される場面では、精度や誤差や丸めなどについて、しっかりと深く理解してから注意してプログラムを書く必要があります。
一応は、VCSSLにも十進で多倍長計算を行うためのデータ型( varfloat型 )が用意されているのですが、 具体的にふみ込むには、そのような難しい説明が必要になってしまうので、ここでは紹介だけにとどめておきましょう。
さて、いよいよ今回の最後です。実はデータ型は、整数と小数だけではありません。 たとえば 前回、「 文字列 」について少しだけ説明しました。 「 "ABC" 」のように文章を「 " 」記号 ではさめば、 その間は「 文字が並んだデータ 」、つまり文字列と見なされるのでしたね。 この「文字列」というのも、一種のデータ型です(※)。確かに文字列は、整数や小数とは全然種類が違うものなので、データとしても区別して扱う必要がありますね。
( ※ 文字列を扱うデータ型やクラスなどが、標準で存在するかどうかは、プログラミング言語によって異なります。 例えばC言語では、1個の文字を扱うデータ型はありますが、文字列全体を扱うデータ型はありません。 そのため、C言語において文字列のデータは、個々の文字のデータが並んだものとして扱われます。)
ところで、文字列に対しては引き算やかけ算・割り算などは行えないのですが、実は足し算だけは行えます。 ただし、その振る舞いは、整数や小数とは全く違うものになります。 試してみましょう:
このように文字列同士を足すと、その結果は、文字列を結合したものになります。 実際の実行結果は以下の通りです:
確かに文字列が結合されていますね。 同様に、文字列と数値を足す事もできます:
このような場合、まず数値「 123 」が文字列「 "123" 」に変換された上で、結合されます。 実際の実行結果は以下の通りです:
文字列と数値を足した結果の型は、数値が整数か小数かを問わず、必ず文字列になります。 これも、数値同士の足し算とは違う振る舞いですね。
ここまで見てきたように、足し算や割り算などの演算子の振る舞いが、データ型に応じて変化してしまう事は、 まぎらわしく感じるかもしれませんが、しかしデータ型の重要な役割の一つでもあります。
小学校の算数で「 ABC + DE = ? 」といった計算を習わない通り、そもそも意味的に、文字列に対して数値の足し算と同じ事はできないはずです。 なので、もしコンピューターが、文字列のデータに対して数値の足し算と同じ処理を行ってしまったら、その結果のデータは意味不明なものになってしまいます。
同様に、数値でも小数点の有無によって計算のやり方は違うので(実際に学校でも別々に習いますね)、 小数のデータに対して整数の演算と全く同じ処理を行ってしまうと、やはりその結果のデータはおかしなものになります。
したがって、ちゃんとデータの種類に応じて、意味のある処理をコンピューターに行ってもらう必要があり、データ型はそのための重要な役割を担っているのです。