例えばゲームなど、 3DCGの舞台を動き回るようなプログラムの開発において、重要な役割を担うのが、衝突判定の処理です。

衝突判定とは、その名前の通り、立体同士の衝突を判定するための処理です。例えば3DCGの舞台を動き回るようなプログラムでは、主人公と地面、または壁などとの衝突判定が必要不可欠となります。主人公が地面と衝突している際はそれ以上落下しないように、また壁と衝突した際は垂直に押し戻されるように、衝突判定を使用して適切な処理を行う必要があります。

直線とポリゴンとの衝突判定

VCSSL Graphics3Dにおいて、衝突判定の基本となるのが、直線とポリゴンとの衝突判定です。これは、任意の原点と方向を持つ直線（原点から一方向にのみ無限に伸びる、いわゆる半直線）と、ポリゴンとが交点を持つかどうかという判定です。

なお、直線とポリゴンとが交点を持つ場合には、その交点の位置と、交点におけるポリゴンの法線ベクトル（ポリゴンに垂直な方向を持ち、大きさが1のベクトル）の情報も得たい場合が多いでしょう。

直線とポリゴンとの交点位置や法線ベクトルは、高校数学の教科書に載っているような公式で独自に求める事もできますが、 VCSSL Graphics3Dではあらかじめ用意されている getPolygonIntersection 関数で簡単に求める事が可能です。

この関数はポリゴンと直線との位置関係を解析し、交点が存在すれば true を、存在しなければ false を返します。

交点が存在する場合は、引数に指定された intersectionVectorID のベクトルに交点位置ベクトルが、 normalVectorID のベクトルに法線ベクトル（※）が代入されます。これらのベクトルは、あらかじめ生成しておく必要がありますが、成分はこの関数によって書き換えられるため、何でも構いません。

直線とモデルとの衝突判定

モデルはポリゴンの集合体なので、直線とモデルとの衝突判定は、直線とポリゴンとの衝突判定の繰り返しで行う事ができます。つまりモデルを構成するすべてのポリゴンに対して、直線との衝突判定を行います。交点が複数存在する場合は、直線の原点に最も近い交点を検索します。この処理はあらかじめ関数として用意されています。

モデルをポリゴンとの衝突判定を行うには、 getModelIntersection 関数を使用します。

この関数はモデルと直線との位置関係を解析し、交点が存在すれば true を、存在しなければ false を返します。

交点が存在する場合は、引数に指定された intersectionVectorID のベクトルに交点位置ベクトル情報が、 normalVectorID のベクトルに法線ベクトル情報が代入されます。交点が複数存在する場合は、直線の原点位置（ pointVectorID で指定）に最も近いものが選択されます。

ポリゴン同士の衝突判定

ポリゴン同士やモデル同士になると、衝突判定は複雑になり、様々なやり方や工夫を要するようになります。

その一例として、直線とポリゴンとの衝突判定を応用して、ポリゴン同士の衝突判定を行う方法を紹介しておきましょう。簡単のため、ポリゴンは三角形であるものとします。

他にも色々な方法が考えられますが、とりあえず上記の方法で判断できます。

モデル同士の衝突判定

続いて、モデル同士の衝突判定をどうやるかについて考えてみましょう。これも単純な話ではなく、工夫が必要です。

まず一番単純に思いつく方法としては、モデルを構成するポリゴン同士の接触判定を、あらゆるポリゴンの組に対して行うのはどうでしょう。直方体などの、ポリゴン数が少ないモデル同士については、それでも意外と有用かもしれません。

しかし例えば1万ポリゴンのモデル同士の場合、ポリゴンの組は1万×1万=1億通りもできてしまい、素直に衝突判定を行っていたのでは、相当重い処理になってしまいます。

もっとポリゴン数が多いモデルもざらにあるため、モデル同士の場合は、ある程度処理を簡略化する必要が生じてくるでしょう。以下に、その典型例をいくつか紹介しておきます。

モデル同士の距離で判定（バウンディングスフィア）

手軽な方法として挙げられるのが、モデル同士の中心間距離で衝突判定を行う方法（バウンディングスフィア）です。モデルの中心が原点になるように、モデルをそれぞれ座標系に配置し、あとは座標系の原点位置が一定の距離内に接近したら衝突と見なします。この方法は非常に軽い負荷で処理する事が可能なので、大量のモデル同士のおおまかな衝突判定に向いているでしょう。

適当な箇所から半直線（レイ）を伸ばし、ポリゴンとの交点で判定

もう少し詳細な衝突判定として、半直線（レイ）との交点で衝突判定を行う事も考えられます。まず、モデルの形状を考慮した上で、でっぱった箇所の先端など、ある程度衝突しそうな箇所から、衝突しそうな方向へ半直線を延ばします。そして、この半直線と別のモデルとの交点が、一定以上近い距離に存在する場合に、モデル同士が衝突したと見なします。

描画用のモデルとは別に、衝突判定用の荒い形状を別に作る（バウンディングボックスなど）

描画用の細かい形状のモデルを囲むように、おおまかな衝突判定用の形状を作るのも有用でしょう。 VCSSLでは、これは透明なポリゴンやモデルを作って、描画用モデルに重ねて配置するなどで対応できます。衝突用の形状は、例えば直方体（バウンディングボックス）などが考えられます。

プログラム例

実際にワールド座標系上に箱型モデルを配置し、上から点を落下させ、箱型表面ではね返してみましょう。これには直線とモデルとの衝突判定を用います。具体的には、落下する点から下向きに半直線を延ばし、それとモデルとの交点が一定以内の距離に来ると、落下速度の向きを反転させてはね返します。以下のように記述し、実行してみてください。


import graphics3d.Graphics3DFramework;
import Graphics3D;
import Math;  // abs関数を使用するため


// モデルやポリゴンのIDを控えておく変数
int axis, box, pointPolygon;

// ベクトルのIDを控えておく変数
int directionVector, pointVector, interVector, normalVector; 

// アニメーションや運動に関する変数
double y = 3.0; // 点の高度
double v = -0.0; // 点の速度
double a = -1.0; // 重力加速度
double dt = 0.05; // 運動のアニメーション時間間隔


// プログラムの最初に呼び出される関数
void onStart ( int rendererID ) {

	// 画面サイズや背景色の設定（省略可能）
	setWindowSize( 800, 600 );
	setBackgroundColor( 0, 0, 0, 255 );

	// ワールド座標系上に座標軸モデルを配置
	axis = newAxisModel( 3.0, 3.0, 3.0 );
	mountModel( axis, rendererID );

	// 点の運動を見るため、点ポリゴンを配置
	pointPolygon = newPointPolygon( 0.0, 0.0, 0.0, 0.1 );
	mountPolygon( pointPolygon, rendererID );

	// ワールド座標系上に箱形モデルを配置
	box = newBoxModel( 1.0, 1.0, 1.0 );
	mountModel( box, rendererID );

	// 衝突判定直線の方向ベクトルを用意
	directionVector = newVector( 0.0, -1.0, 0.0 );

	// 衝突判定直線の原点ベクトルを用意
	pointVector = newVector( 0.0, 3.0, 0.0 );

	// 交点格納用のベクトルを用意
	interVector = newVector();

	// 法線格納用のベクトルを用意
	normalVector = newVector();
}


// 画面更新周期ごとに毎秒数十回呼び出される関数
void onUpdate (int renderer) {

	// 落下する点の位置を計算
	v += a * dt;
	y += v * dt;

	// 点ポリゴンの位置と衝突判定直線の原点位置を更新
	setVector( pointVector, 0.0, y, 0.0 );
	setPolygonVector( pointPolygon, 0.0, y, 0.0 );

	// 衝突判定、戻り値は交点の有無
	bool hit = getModelIntersection( 
			box, directionVector, pointVector, interVector, normalVector
	);

	// 交点が存在し、距離が0.2以内なら速度反転して跳ね返す
	if( hit ){
			// abs関数は絶対値を返す関数
			if( abs( getVectorY( interVector ) - y ) < 0.2 ){
					v = abs( v );
			}
	}
}

Sample.vcssl

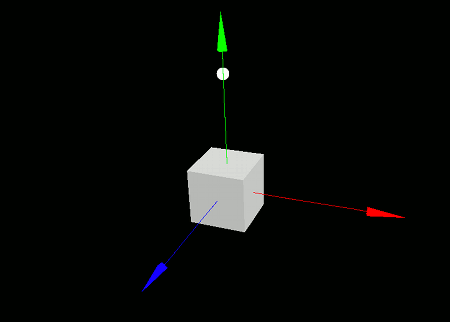
このプログラムを実行すると、画面に白い箱とボールが表示されます。ボールは落下していき、ボールの表面で跳ね返ります。

※ 上の処理は、あくまでも単純な実装例で、「箱の表面でボールの飛ぶ向きを反転させる」という事しか行っていないため、抜け穴がいくつもあります。

実際、しばらく放置すると、落下運動の計算誤差によってボールの勢いが弱まっていき、やがて箱にゆっくり接してめり込んでいってしまいます。いわゆるゲームでの「壁抜けバグ」みたいな現象ですね。

当たり判定において、こういう現象を片っ端から潰していくのは意外と面倒です。なので、ここでは割愛します。