ベクトルの成分と座標系
基準となる座標系が異なれば、同じ位置を指し示すベクトルの成分も異なる。
ここでは、ベクトルやポリゴン、 モデルの座標変換について扱います。
前回紹介したベクトル関連の関数は、 主に立体の位置関係を把握するために使用します。 例えば、ある位置を別の座標系から見るとどの位置になるかを求めたり、 モデルとベクトルとの交点を求めたりするなどの用途が挙げられます。
さて、複数の座標系にまたがった位置関係を把握したい場合、ベクトルの成分値をそのまま参照するだけでは駄目で、一種の変換処理が必要になります。
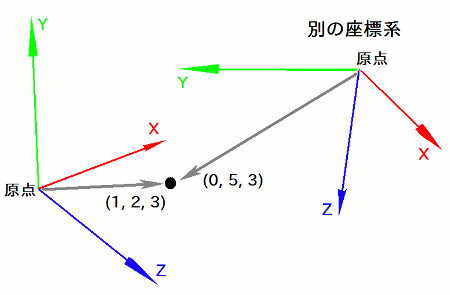
なぜなら、異なる座標系では、 一般に原点の位置や座標軸の方向も異なるため、同じ点を指すベクトルの成分値も異なるためです。例えばある座標系から見た（ 1, 2, 3 ）は、 別の座標系から見た（ 0, 5, 3 ）かもしれません。
つまりベクトルの成分に格納された値は、 そのベクトルが配置されている座標系でしか意味を持ちません。 ベクトルの成分と座標系は常にワンセットで考えるべきなのです。
そして、「ある座標系上のベクトルが指す点を、別の座標系基準の成分で表したい」という場面はよく生じます。これがまさに、「座標変換」と呼ばれる処理です。
例えば、「異なる座標系に属する2点間の距離を知りたい」といった場合には、それぞれの点を指すベクトルを、共通の座標系上に座標変換してから、距離を求める必要があります。
- 関数の形式 -
引数は以下の通りです：
ポリゴンも、頂点の位置を表すベクトルを内部に保持しています。 従ってポリゴンの位置関係を計算するには、 ポリゴンを構成するベクトルもまとめて座標変換する必要があります。
ポリゴンを座標変換するには、 transformPolygon 関数を使用します。
- 関数の形式 -
引数は以下の通りです：
引数 polygonID に渡すポリゴンと、bufferID に渡すポリゴンの種類が異なると、正常に変換できないため注意が必要です。bufferID に、modelID のモデルのコピーを渡すのは、その問題を生じないようにするためです。
モデルも多数のポリゴンで構成されているため、 大量のベクトルを内部に保持しています。 従ってモデルの位置関係を計算するには、 モデルを構成するベクトルもまとめて座標変換する必要があります。
モデルを座標変換するには、 transformModel 関数を使用します。
- 関数の形式 -
引数は以下の通りです：
引数 modelID に渡すモデルと、bufferID に渡すモデルのポリゴン数や超点数が異なると、正常に変換できないため注意が必要です。bufferID に、modelID のモデルのコピーを渡すのは、その問題を生じないようにするためです。
実際にローカル座標系上にベクトルを配置し、 ワールド座標系に座標変換してみましょう。 以下のように記述し、実行してみてください。
import graphics3d.Graphics3DFramework;
import Graphics3D;
import Math; // 円周率(PI)の値を使用するため
// プログラムの最初に呼び出される関数
void onStart ( int rendererID ) {
// ローカル座標系を生成
int coord = newCoordinate( );
// ローカル座標系をワールド座標系に配置
mountCoordinate( coord, rendererID );
// ローカル座標系をZ軸まわりに45度回転
rotCoordinateZ( coord, PI/4.0 );
// X=1.0のベクトルを生成
int vector = newVector( 1.0, 0.0, 0.0 );
// ローカル座標系上にベクトルを配置
mountVector( vector, rendererID, coord );
// 座標変換結果の控え用に、vectorのコピーを生成
int trans = newVector( vector );
// vectorをワールド座標系へ座標変換し、結果をtransに代入
transformVector(
vector, trans, getWorldCoordinate( rendererID )
);
// 座標変換結果を出力
println(
getVectorX( trans ), getVectorY( trans ), getVectorZ( trans )
);
}
このプログラムでは、Z軸まわりに45度だけ回転したローカル座標系上に （ X, Y, Z ） = （ 1.0, 0.0, 0.0 ） のベクトルを配置し、それをワールド座標系に座標変換した結果を、 VCSSLコンソールに出力しています。
このプログラムを実際に実行すると、VCSSLコンソールに