
ここでは、立体モデルの生成と配置方法、および色々な種類の標準立体モデルについて扱います。
モデルとは、3次元の形状を表現するもので、 ポリゴンという微小な多角形の集合で構成されています。 ペーパークラフトのようなものを想像するとよいかもしれません。

例えば球モデルは、上の図の通り、ちょうど地球儀の経線と緯線で囲まれる四角形の集合のように、 規則正しく並んだ大量の四角形ポリゴンで構成されています(※)。
VCSSLでは、自分で独自にポリゴンの集合を生成してモデルにまとめる事もできますが、 基本的な形状を表現するモデルは標準で用意されています。
これからしばらくは、この標準モデルを中心に扱っていきます。
標準モデルを生成するには、 new〜Model 関数を使用します。 〜の部分には標準モデル固有の名称が入ります。 標準モデルには様々な種類が存在しますが、 各モデルの具体的な生成に関しては、すぐ後のセクションで扱います。
- 関数の形式 -
この関数は標準モデルを生成し、そのモデルのIDを返します。
自分で生成したポリゴンの集合からモデルを生成するには、 newModel 関数を使用します。 なお、ポリゴンの生成や制御に関しては、次の回で扱います。
- 関数の形式 -
引数は以下の通りです:
この関数は、受け取ったポリゴンの集合を一つのモデルにまとめ、 そのモデルのIDを返します。ポリゴン集合をモデルにまとめる利点は、平行移動や回転などを一括して行えるようになる事です。
newModel 関数では、すでに生成したモデルをコピーし、 同型の新しいモデルを作る事も可能です。
- 関数の形式 -
引数 copyModelID に、コピーしたいモデルのモデルIDを指定します。
生成したモデルを配置するには、 mountModel 関数を使用します。
- 関数の形式 -
引数は以下の通りです:
なお、次のように座標系を指定して配置する事も可能です。 座標系に関しては、本ガイドの後半で扱います。
- 関数の形式 -
引数modelIDには配置するモデルのIDを、 続く引数rendererIDにはレンダラーのID、 最後の引数coordinateIDには座標系のIDを指定します。
それでは、VCSSLでサポートされている、各種の標準モデルと生成関数を見ていきましょう。
以下で解説する関数は全て、戻り値として、生成したモデルのIDを返します。
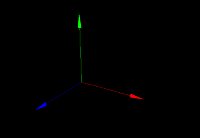
座標軸(アクシス)モデルは、3次元空間の方向を指し示すモデルです。 3DCGの舞台設計は、最初にこの座標軸モデルを配置する事から始まるとも言える、 非常に重要なモデルです。
座標軸モデルを生成するには、 newAxisModel 関数を使用します。
- 関数の形式 -
引数は以下の通りです:

球(スフィア)モデルを生成するには、 newSphereModel 関数を使用します。
- 関数の形式 -
引数は以下の通りです:
※ モデル全体のポリゴン数は n1 × n2 となります。
ポリゴン数とは、曲面を表現するのに使用するポリゴンの数です。 ポリゴン数を上げるほど曲面がなめらかに、下げるほどカクカクになります。
なお、このモデルの配置時には、中心(重心)が座標系の原点に一致するよう配置されます。

直方体モデル(ボックス)を生成するには、newBoxModel関数を使用します。
- 関数の形式 -
引数は以下の通りです:
このモデルの配置時には、中心(重心)が座標系の原点に一致するよう配置されます。言語やライブラリによっては、端(頂点)のどれかが原点に一致するように配置されるものもあるため、差異に留意が必要です。

円柱(シリンダー)モデルを生成するには、 newCylinderModel 関数を使用します。
- 関数の形式 -
引数は以下の通りです:
このモデルの配置時には、底面の中心が原点に一致するよう配置されます。

底面なしの円筒(チューブ)モデルを生成するには、 newTubeModel関数を使用します。
- 関数の形式 -
引数は以下の通りです:
このモデルの配置時には、底面の中心が原点に一致するよう配置されます。

円錐(コーン)モデルを生成するには、 newConeModel 関数を使用します。
- 関数の形式 -
引数は以下の通りです:
このモデルの配置時には、底面の中心が原点に一致するよう配置されます。

底面なしの円錐(シェード)モデルを生成するには、 newShadeModel 関数を使用します。
- 関数の形式 -
引数は以下の通りです:
このモデルの配置時には、底面の中心が原点に一致するよう配置されます。

円盤(ディスク)モデルを生成するには、 newDiskModel 関数を使用します。
- 関数の形式 -
引数は以下の通りです:
このモデルの配置時には、円盤の中心が原点に一致するよう配置されます。
ところで、モデルを構成するポリゴンの面には、表面と裏面があります。そして、裏面も描画するように設定しない限り、通常は表面しか描画されません。 これは、見える必要がない面の処理を省いて、描画負荷を軽減する(または高速化する)ためです。
例えば、すぐ上で扱った円盤モデルでは、 生成時にZ軸の上の方が表面となります。つまり、Z軸の下の方から見ても、そちら側は裏面なので、なにも見えません。 そこで
のように設定する事で、裏面の描画省略機能を無効化し、どちら側の面からも見えるようにできます。 ここで modelID には、設定対象のモデルのIDを指定します。
それでは、上で扱った各種標準モデルを実際に使用してみましょう。 以下のように記述し、実行してみてください。
import graphics3d.Graphics3DFramework;
import Graphics3D;
// プログラムの最初に呼び出される関数
void onStart ( int rendererID ) {
// 画面サイズや背景色の設定(省略可能)
setWindowSize(800, 600);
setBackgroundColor(0, 0, 0, 255);
// 座標軸モデルを生成して配置
int axis = newAxisModel( 3.0, 3.0, 3.0 );
mountModel( axis, rendererID );
// 球モデルを生成して配置
int sphere = newSphereModel( 0.5, 0.5, 0.5, 10, 7 );
mountModel( sphere, rendererID );
// 直方体モデルを生成して配置
int box = newBoxModel( 1.0, 1.0, 1.0 );
mountModel( box, rendererID );
moveModel( box, 1.25, 0.0, 0.0 ); // 平行移動
// 円柱モデルを生成して配置
int cylinder = newCylinderModel( 0.5, 0.5, 1.0, 20, 1 );
mountModel( cylinder, rendererID );
moveModel( cylinder, 2.5, 0.0, 0.0 ); // 平行移動
// 底面なしの円筒モデルを生成して配置
int tube = newTubeModel( 0.5, 0.5, 1.0, 20, 1 );
mountModel( tube, rendererID );
moveModel( tube, 0.0, 1.25, 0.0 ); // 平行移動
// setModelCull( tube, false, false ); // 内側の面も見えるようにしたい場合
// 円錐モデルを生成して配置
int cone = newConeModel( 0.5, 0.5, 1.0, 20, 1 );
mountModel( cone, rendererID );
moveModel( cone, 1.25, 1.25, 0.0 ); // 平行移動
// 底面なしの円錐モデルを生成して配置
int shade = newShadeModel( 0.5, 0.5, 1.0, 20, 1 );
mountModel( shade, rendererID );
moveModel( shade, 2.5, 1.25, 0.0 ); // 平行移動
// setModelCull( shade, false, false ); // 内側の面も見えるようにしたい場合
// 円盤モデルを生成して配置
int disk = newDiskModel( 0.5, 0.5, 20 );
mountModel( disk, rendererID );
moveModel( disk, 0.0, 2.5, 0.0 ); // 平行移動
// setModelCull( disk, false, false ); // 裏面も見えるようにしたい場合
}
このプログラムを実行すると、黒い背景に様々な標準モデルが表示されます。

なお、円筒の内側は裏面なので、標準では描画されません。描画するには、円筒モデル生成後にある「 setModelCull( tube, false, false ); 」の行のコメントアウトを外し、裏面の描画省略を無効化してください。 底面なしの円錐モデルや、円盤モデルなどについても同様です。