Walking Coordinate Systems

This section introduces the concept of walking a coordinate system. In this context, "walking" refers to a type of movement -- but unlike standard movement based on the parent coordinate system's axes, walking is movement based on the coordinate system's own axes.

Walking a Coordinate System

To walk a coordinate system, use the walkCoordinate(...) function.

- Function Format -

Arguments:

• coordinateID: Specifies the ID of the coordinate system to walk.
• dx, dy, dz: Specify the distances to move in the X, Y, and Z directions, relative to the coordinate system's own axes.

Example Program

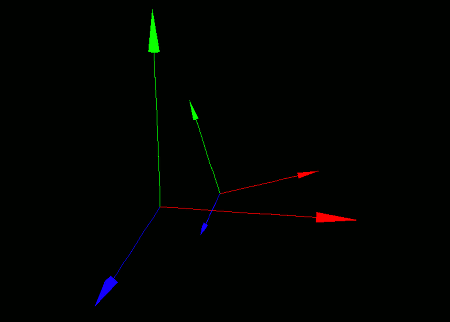
Let's walk a local coordinate system placed on top of the world coordinate system. To clearly distinguish the two, we'll place a small axis model on the local coordinate system and a large one on the world coordinate system.

To highlight the difference between walking and standard movement (via moveCoordinate), we'll first rotate the local coordinate system slightly around the Z-axis before walking it.

import graphics3d.Graphics3DFramework;
import Graphics3D;

// Function called at the start of the program
void onStart ( int rendererID ) {

	// (Optional) Set window size and background color
	setWindowSize( 800, 600 );
	setBackgroundColor( 0, 0, 0, 255 );


	// Create a local coordinate system
	int coord = newCoordinate( );

	// Mount the local coordinate system onto the world coordinate system
	mountCoordinate( coord, rendererID );

	// Rotate the local coordinate system slightly around the Z-axis
	rotCoordinateZ( coord, 0.3 );

	// Walk the local coordinate system
	walkCoordinate( coord, 1.0, 0.0, 0.0 );

	// Place a small axis model on the local coordinate system
	int axis1 = newAxisModel( 1.5, 1.5, 1.5 );
	mountModel( axis1, rendererID, coord );

	// Place a large axis model on the world coordinate system
	int axis2 = newAxisModel( 3.0, 3.0, 3.0 );
	mountModel( axis2, rendererID );
}

When you run this program, you'll see two axis models on a black screen: The large one is placed on the world coordinate system, while the small one is placed on the local coordinate system.

The local coordinate system is shown at a position offset by (1.0, 0.0, 0.0) relative to its own axes.

Execution Result

The small one appears slightly shifted in the direction of its own X-axis.