Vector Components and Coordinate Systems
If the reference coordinate system changes, the same position will be represented by different vector components.
This section covers how to perform coordinate transformations for vectors, polygons, and models.
The vector-related functions introduced in the previous section are mainly used for understanding spatial relationships between 3D objects. For example, you might want to determine where a certain position would appear from the perspective of a different coordinate system, or find the intersection between a model and a vector.
When handling positions that span multiple coordinate systems, you can't simply compare raw vector components -- you need to perform a transformation.
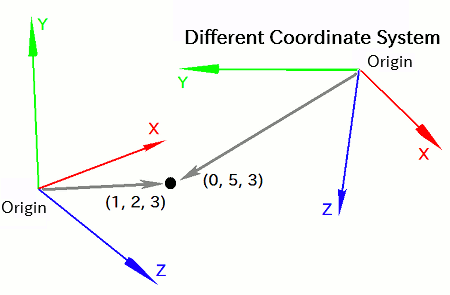
This is because in different coordinate systems, the origin and axis orientations generally differ. As a result, a vector pointing to the same position in space may have different component values depending on the coordinate system.
For example, the point (1, 2, 3) in one system might appear as (0, 5, 3) in another.
In other words, the component values of a vector are only meaningful in the context of the coordinate system in which it is defined. A vector and its coordinate system should always be treated as a pair.
It is often necessary to express the position indicated by a vector in one coordinate system using the components of another. This process is what we call coordinate transformation.
For instance, if you want to calculate the distance between two points that belong to different coordinate systems, you first need to transform both vectors to a common coordinate system before measuring the distance.
- Function Format -
Arguments:
Polygons internally store vectors representing the positions of their vertices.
Therefore, to compute spatial relationships involving polygons, you need to transform all vectors that make up the polygon.
To transform a polygon, use the transformPolygon function:
- Function Format -
Arguments:
Since models are composed of many polygons, they internally contain a large number of vectors.
To compute spatial relationships involving models, you also need to transform all vectors that make up the model.
To transform a model, use the transformModel(...) function:
- Function Format -
Arguments:
Let's create a local coordinate system, place a vector within it, and transform that vector into the world coordinate system.
Write the following code and run it:
import graphics3d.Graphics3DFramework;
import Graphics3D;
import Math; // for using the constant PI
// Function called at the start of the program
void onStart ( int rendererID ) {
// Create a local coordinate system
int coord = newCoordinate( );
// Mount it onto the world coordinate system
mountCoordinate( coord, rendererID );
// Rotate the local coordinate system 45 degrees around the Z axis
rotCoordinateZ( coord, PI/4.0 );
// Create a vector with X = 1.0
int vector = newVector( 1.0, 0.0, 0.0 );
// Place the vector on the local coordinate system
mountVector( vector, rendererID, coord );
// Create a copy of the vector to store the transformation result
int trans = newVector( vector );
// Transform the vector into the world coordinate system
transformVector(
vector, trans, getWorldCoordinate( rendererID )
);
// Output the result
println(
getVectorX( trans ), getVectorY( trans ), getVectorZ( trans )
);
}
This program places the vector (X, Y, Z) = (1.0, 0.0, 0.0) in a local coordinate system that is rotated 45 degrees around the Z axis, then transforms it into the world coordinate system and prints the result to the VCSSL console.
When you run the program, the VCSSL console will display:
The transformed X and Y values are both equal to 1/√2, confirming that the transformation was performed correctly.