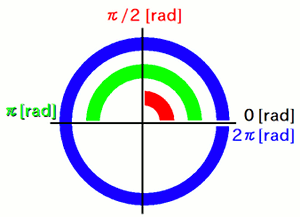
A radian is a unit of angular measure commonly used in science and engineering. In this unit system, 180 degrees is equivalent to π radians. For example, 90 degrees = π/2 radians, and 45 degrees = π/4 radians.
This section covers how to spin coordinate systems. Here, "spinning" refers to rotations based on the axes of the coordinate system itself, rather than those of its parent system.
To spin a coordinate system around its own X, Y, or Z axis, use the spinCoordinateX(...), spinCoordinateY(...), and spinCoordinateZ(...) functions:
- Function Format -
These three functions handle rotation around the local X, Y, and Z axes, respectively.
Arguments:

To spin a coordinate system around an axis defined by a direction vector (relative to itself), use the spinCoordinate(...) function:
- Function Format -
Arguments:
To spin a coordinate system around an axis that has both an arbitrary origin and direction (from the perspective of the coordinate system itself), use an extended form of spinCoordinate(...):
- Function Format -
Arguments:
Let's place a local coordinate system on top of the world coordinate system and spin it 45 degrees (π/4 radians) around its own Z axis.
To help visualize the result, a small axis model will be mounted on the local system, and a large one on the world system. To make the difference between spinning and rotating clearer, we'll move the local coordinate system slightly in the X direction before spinning it.
import graphics3d.Graphics3DFramework;
import Graphics3D;
import Math; // For the PI constant
// Function called at the start of the program
void onStart ( int rendererID ) {
// Optional screen size and background color settings
setWindowSize( 800, 600 );
setBackgroundColor( 0, 0, 0, 255 );
// Create a local coordinate system
int coord = newCoordinate( );
// Mount it on the world coordinate system
mountCoordinate( coord, rendererID );
// Move the local system slightly in the X direction
moveCoordinate( coord, 1.0, 0.0, 0.0 );
// Spin the local system 45 degrees around its own Z axis
spinCoordinateZ( coord, PI/4.0 );
// Mount a small axis model on the local system
int axis1 = newAxisModel( 1.5, 1.5, 1.5 );
mountModel( axis1, rendererID, coord );
// Mount a large axis model on the world system
int axis2 = newAxisModel( 3.0, 3.0, 3.0 );
mountModel( axis2, rendererID );
}
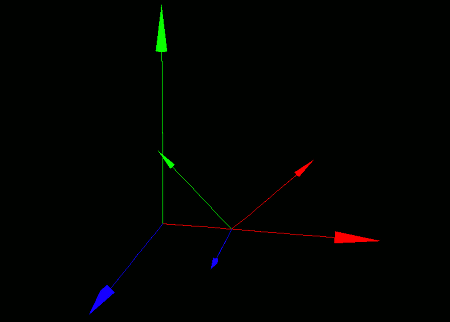
When this program is executed, a black screen will display two axis models. The larger one is mounted on the world coordinate system, and the smaller one is on the local system. The local coordinate system is moved 1.0 unit along the parent's X axis, and then spun 45 degrees around its own Z axis.