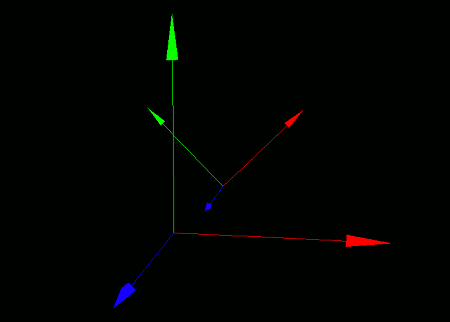
A radian is a unit of angular measure commonly used in science and engineering. In this unit system, 180 degrees is equivalent to π radians. For example, 90 degrees = π/2 radians, and 45 degrees = π/4 radians.
This section covers how to rotate coordinate systems.
The type of rotation discussed here is based on the axes of the parent coordinate system. For rotations based on the axes of the coordinate system itself, see the next section: Spinning a Coordinate System.
To rotate a coordinate system around one of the parent system's axes (X, Y, or Z), use the rotCoordinateX(...), rotCoordinateY(...), and rotCoordinateZ(...) functions:
- Function Format -
These three functions handle rotation around the X, Y, and Z axes, respectively.
Arguments:

To rotate a coordinate system around an axis pointing in an arbitrary direction (as seen from the parent system), use the rotCoordinate(...) function:
- Function Format -
Arguments:
To rotate around an axis defined not only by direction but also by an arbitrary origin (relative to the parent system), use an extended form of the rotCoordinate(...) function:
- Function Format -
Arguments:
Let's create a local coordinate system, place it on top of the world coordinate system, and rotate it by 45 degrees (π/4 radians).
To help visualize the difference between local and world systems, we'll mount a smaller axis model on the local system and a larger one on the world system.
Also, to distinguish this kind of rotation from self-rotation (which will be covered next), we'll first move the local coordinate system slightly in the X direction before applying the rotation.
import graphics3d.Graphics3DFramework;
import Graphics3D;
import Math; // For accessing the PI constant
// Function called at the start of the program
void onStart ( int rendererID ) {
// Optional screen size and background color settings
setWindowSize( 800, 600 );
setBackgroundColor( 0, 0, 0, 255 );
// Create a local coordinate system
int coord = newCoordinate( );
// Mount it on the world coordinate system
mountCoordinate( coord, rendererID );
// Move the local system slightly along the X axis
moveCoordinate( coord, 1.0, 0.0, 0.0 );
// Rotate the local system 45 degrees (π/4 radians) around the Z axis
rotCoordinateZ( coord, PI/4.0 );
// Mount a small axis model on the local system
int axis1 = newAxisModel( 1.5, 1.5, 1.5 );
mountModel( axis1, rendererID, coord );
// Mount a large axis model on the world system
int axis2 = newAxisModel( 3.0, 3.0, 3.0 );
mountModel( axis2, rendererID );
}
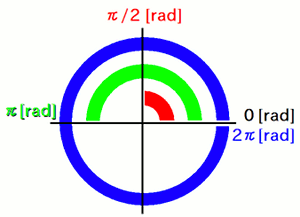
When you run this program, you'll see two axis models on a black screen.
The large model is mounted on the world coordinate system, and the small model is mounted on the local coordinate system. The local system is first moved 1.0 unit in the parent system's X direction, then rotated 45 degrees around the parent system's Z axis.