Creating and Placing 3D Models (Standard Model Types Included)

This section explains how to create and place 3D models, focusing on the various built-in standard models provided by VCSSL.

Sponsored Link

What Is a Model?

A model represents a three-dimensional shape, constructed from a collection of small polygons. You can think of it like a paper craft made of many flat pieces assembled into a 3D form.

Polygon Mesh of a Sphere Model

A sphere model consists of a regular grid of rectangular polygons, much like the pattern formed by the meridians and parallels on a globe.

For example, as shown above, a sphere model in VCSSL is made up of a large number of rectangles, arranged in a pattern similar to the lines of latitude and longitude on a globe. (*)

While you can generate your own custom polygon groups to build models in VCSSL, a variety of basic shape models are already available as standard.

In this section and those that follow, we�fll focus on working with these standard models.

Creating Models

Creating Standard Models

To create a standard model, use one of the "new...Model" functions, where "..." is the name of the specific model type.

- Function Format -

This function generates the specified model and returns a model ID that you can use to manipulate or place the model.

Creating Custom Models

To create a model from your own collection of polygons, use the newModel(...) function. Polygon creation and manipulation will be covered in the next section.

- Function Format -

Arguments:

• polygonIDs: An array of polygon IDs that make up the model.

This function combines the specified polygons into a single model and returns its model ID. The advantage of grouping polygons into a model is that you can perform transformations like translation and rotation on the entire model at once.

Creating a Copy of a Model

The newModel(...) function can also be used to duplicate an existing model.

- Function Format -

Argument:

• copyModelID: The ID of the model to copy.

This will create a new model with the same shape as the one specified.

Placing Models

To place a model in the 3D scene, use the mountModel(...) function.

- Basic Function Format -

Arguments:

• modelID: The ID of the model to place.
• rendererID: The ID of the renderer responsible for drawing the model.

You can also specify a coordinate system for placement (coordinate systems will be covered later in this guide):

- Extended Function Format -

Arguments:

• modelID: The ID of the model to place.
• rendererID: The ID of the renderer.
• coordinateID: The ID of the coordinate system where the model should be placed.

Standard 3D Models

Now let's look at the various built-in standard models supported by VCSSL and how to create them.

All of the functions described below return a model ID as their return value.

Axis Model

Axis Model

Red represents the X-axis, green the Y-axis, and blue the Z-axis -- corresponding to (X, Y, Z) = (R, G, B).

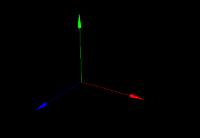
The axis model is used to indicate directions in 3D space. You could say that setting up a 3DCG scene begins by placing this model -- it's a very important element for spatial reference.

To create an axis model, use the newAxisModel(...) function:

- Function Format -

Arguments:

• xLength, yLength, zLength: Specify the length of the X, Y, and Z axes respectively.

Sphere Model

Sphere Model

Surface smoothness can be adjusted with n1 and n2.

To create a sphere model, use the newSphereModel(...) function:

- Function Format -

Arguments:

• xRadius, yRadius, zRadius: The radius of the sphere in the X, Y, and Z directions.
• n1: Number of polygon divisions along lines of latitude (i.e., longitudinal segments).
• n2: Number of polygon divisions along lines of longitude (i.e., latitudinal segments).

Note: The total number of polygons used will be n1 �~ n2.

The more polygons used, the smoother the surface becomes; fewer polygons will make it appear more faceted. This model is placed such that its center (centroid) aligns with the origin of the coordinate system.

Box Model

Box Model

Each face is constructed from a single polygon.

To create a box (rectangular prism) model, use the newBoxModel(...) function:

- Function Format -

Arguments:

• xLength, yLength, zLength: Specify the size in the X, Y, and Z directions.

This model is placed so that its center (centroid) aligns with the origin. Note that some libraries or languages may define the model such that a corner or face aligns with the origin, so be aware of this difference.

Cylinder Model

Cylinder Model

Surface smoothness can be adjusted with n1 and n2.

To create a cylinder model, use the newCylinderModel(...) function:

- Function Format -

Arguments:

• xRadius, yRadius: Radius of the cylinder in the X and Y directions.
• zLength: Length (height) of the cylinder along the Z axis.
• n1: Number of polygon divisions around the circumference.
• n2: Number of polygon divisions along the Z axis.

This model is placed such that the center of its bottom face aligns with the origin.

Tube Model: Open-Ended Cylindrical (Tube) Model

Tube Model

Surface smoothness can be adjusted with n1 and n2.

To create an open-ended cylindrical (tube) model, use the newTubeModel(...) function:

- Function Format -

Arguments:

• xRadius, yRadius: Radius of the tube in the X and Y directions.
• zLength: Length (height) of the tube along the Z axis.
• n1: Number of polygon divisions around the circumference.
• n2: Number of polygon divisions along the Z axis.

This model is also placed so that the center of its bottom face aligns with the origin.

Cone Model

Cone Model

Surface smoothness can be adjusted with n1 and n2.

To create a cone model, use the newConeModel(...) function:

- Function Format -

• xRadius, yRadius: Radius in the X and Y directions.
• zLength: Height of the cone (length in the Z direction).
• n1: Number of polygon divisions around the circumference.
• n2: Number of polygon divisions along the Z axis.

This model is placed so that the center of its base aligns with the origin.

Shade Model: Open-Ended Cone Model

Shade Model

Surface smoothness can be adjusted with n1 and n2.

To create an open-ended cone (shade-like) model, use the newShadeModel(...) function:

- Function Format -

Arguments:

• xRadius, yRadius: Radius in the X and Y directions.
• zLength: Height of the cone (length in the Z direction).
• n1: Number of polygon divisions around the circumference.
• n2: Number of polygon divisions along the Z axis.

This model is also placed so that the center of its base aligns with the origin.

Disk Model

Disk Model

Surface smoothness can be adjusted with n. The back side is not rendered.

To create a disk model, use the newDiskModel(...) function:

- Function Format -

Arguments:

• xRadius, yRadius: Radius in the X and Y directions.
• n: Number of polygon divisions used for the disk surface.

The model is placed so that the center of the disk aligns with the origin.

Face Orientation and Backface Culling

Each polygon that forms a model has a front face and a back face.

By default, only the front faces are rendered -- back faces are omitted unless explicitly enabled. This technique is known as backface culling, and it's used to skip rendering surfaces that are not visible from the current viewpoint, reducing rendering cost and improving performance.

For example, the disk model described above has its front face pointing in the positive Z direction upon creation.

If you view it from the negative Z direction, the back face will be invisible due to culling. To make both sides visible, you can disable backface culling like this:

Here, "modelID" is the ID of the model you want to modify.

Example Program

Now, let's try using the standard models introduced above. Write and run the following code:

import graphics3d.Graphics3DFramework;
import Graphics3D;

// The entry point of the program
void onStart ( int rendererID ) {

	// Optional: Set the window size and background color
	setWindowSize( 800, 600 );
	setBackgroundColor( 0, 0, 0, 255 );

	
	// Create and mount an axis model
	int axis = newAxisModel( 3.0, 3.0, 3.0 );
	mountModel( axis, rendererID );

	// Create and mount a sphere model
	int sphere = newSphereModel( 0.5, 0.5, 0.5, 10, 7 );
	mountModel( sphere, rendererID );

	// Create and mount a box model
	int box = newBoxModel( 1.0, 1.0, 1.0 );
	mountModel( box, rendererID );
	moveModel( box, 1.25, 0.0, 0.0 ); // Translate

	// Create and mount a cylinder model
	int cylinder = newCylinderModel( 0.5, 0.5, 1.0, 20, 1 );
	mountModel( cylinder, rendererID );
	moveModel( cylinder, 2.5, 0.0, 0.0 ); // Translate

	// Create and mount a tube (open-ended cylinder) model
	int tube = newTubeModel( 0.5, 0.5, 1.0, 20, 1 );
	mountModel( tube, rendererID );
	moveModel( tube, 0.0, 1.25, 0.0 ); // Translate
	// setModelCull( tube, false, false ); // Uncomment to show the inside surface

	// Create and mount a cone model
	int cone = newConeModel( 0.5, 0.5, 1.0, 20, 1 );
	mountModel( cone, rendererID );
	moveModel( cone, 1.25, 1.25, 0.0 ); // Translate

	// Create and mount a shade (open-ended cone) model
	int shade = newShadeModel( 0.5, 0.5, 1.0, 20, 1 );
	mountModel( shade, rendererID );
	moveModel( shade, 2.5, 1.25, 0.0 ); // Translate
	// setModelCull( shade, false, false ); // Uncomment to show the inside surface

	// Create and mount a disk model
	int disk = newDiskModel( 0.5, 0.5, 20 );
	mountModel( disk, rendererID );
	moveModel( disk, 0.0, 2.5, 0.0 ); // Translate
	// setModelCull( disk, false, false ); // Uncomment to show the back side
}

When you run this program, various standard models will appear on a black background.

Execution Result

A variety of standard models are displayed.

Note that the inside surface of the tube model is considered a back face, so it is not rendered by default. To render the inside, remove the comment from the line "setModelCull(tube, false, false);" after creating the model. The same applies to the shade (open-ended cone) model and the disk model.