Collision Detection

This section covers collision detection between 3D objects.

What Is Collision Detection?

Collision detection plays a crucial role in programs where you move around within a 3D world -- such as in games.

As the name suggests, collision detection is the process of determining whether 3D objects are colliding. For example, in a program where the player walks around a 3D environment, it is essential to detect collisions between the player and the ground or walls. When the player collides with the ground, they must stop falling; when colliding with a wall, they should be pushed back. These behaviors are handled using collision detection.

Collision Detection Between a Ray and a Polygon

In VCSSL Graphics3D, the foundation of collision detection lies in detecting intersections between rays and polygons. This means determining whether a ray -- defined as a line extending infinitely in one direction from a starting point -- intersects with a polygon.

When such an intersection exists, you'll often want to obtain both the position of the intersection and the normal vector at the point of contact (i.e., a unit vector perpendicular to the surface of the polygon).

While it is possible to calculate these values manually using formulas found in high school math textbooks, VCSSL Graphics3D provides a dedicated function to simplify the process: "getPolygonIntersection."

- Function Format -

Parameters:

• polygonID: The ID of the target polygon.
• directionalVectorID: The direction vector of the ray.
• pointVectorID: The starting point vector of the ray.
• intersectionVectorID: A vector to store the intersection point.
• normalVectorID: A vector to store the surface normal at the intersection point.

This function analyzes the relationship between the polygon and the ray. If an intersection exists, it returns true; otherwise, it returns false.

If an intersection exists, the intersection point will be stored in the vector specified by "intersectionVectorID," and the surface normal will be stored in the vector specified by "normalVectorID." These vectors must be created beforehand, but their values will be overwritten by this function, so their initial contents do not matter.

Collision Detection Between a Ray and a Model

A model is made up of multiple polygons, so detecting collisions between a ray and a model is done by checking for intersections with each polygon in the model. If multiple intersection points are found, the one closest to the ray's origin is selected.

VCSSL Graphics3D provides a built-in function for this purpose: getModelIntersection(...).

- Function Format -

Arguments:

• modelID: The ID of the target model.
• directionalVectorID: The direction vector of the ray.
• pointVectorID: The starting point vector of the ray.
• intersectionVectorID: A vector to store the intersection point.
• normalVectorID: A vector to store the surface normal at the intersection point.

This function analyzes the relationship between the model and the ray. If an intersection exists, it returns true; otherwise, it returns false.

If an intersection exists, the closest intersection point to the ray origin (as defined by "pointVectorID") will be stored in "intersectionVectorID," and the corresponding surface normal will be stored in "normalVectorID."

Collision Detection Between Polygons

Collision detection between polygons -- or between models -- is a complex task that requires different strategies and techniques.

One possible approach is to adapt the ray-to-polygon collision detection method for use with polygons. For simplicity, assume that the polygons are triangles.

• First, from each of the triangle's three vertices, cast a ray toward the adjacent vertex. Name these rays V1, V2, and V3. The direction (clockwise or counterclockwise) doesn't matter.
• Next, check for intersections between each of the rays (V1, V2, V3) and another polygon. If an intersection is found for a given ray, calculate the distance from the ray's origin to the intersection point.
• If the distance is shorter than the length of the triangle's corresponding edge, a collision is considered to have occurred. If the distance is longer -- or if no intersection exists -- then there is no collision.

There are many other ways to perform polygon-polygon collision detection, but this method can serve as a basic approach.

Collision Detection Between Models

Let's now consider how to detect collisions between entire models. This is a more complex challenge that often requires various simplifications.

One straightforward (but computationally expensive) approach is to check for collisions between every pair of polygons across both models. This might work fine for low-polygon models such as simple boxes.

However, with high-polygon models -- say, 10,000 polygons each -- the number of combinations becomes overwhelming: 10,000 x 10,000 = 100 million checks. Performing collision detection this way would be extremely inefficient.

Since many models in practical use contain far more polygons, some form of simplification is typically necessary. Here are a few common strategies:

Using Model Center Distance (Bounding Sphere)

A lightweight approach is to detect collisions based on the distance between the centers of models -- a method known as the *bounding sphere* technique. Place each model in its own coordinate system such that its center lies at the origin, then consider a collision to occur if the distance between their origins becomes smaller than a defined threshold. This method is very efficient and well-suited for large-scale, approximate collision detection involving many models.

Casting Rays From Collision-Prone Areas

A slightly more precise approach is to cast rays from parts of the model that are likely to collide -- such as protruding features -- toward likely collision directions. If any of these rays intersect with another model within a certain distance, a collision is assumed to have occurred.

Using Simplified Collision Models (Bounding Boxes, etc.)

Another practical technique is to create simplified collision models that roughly envelop the detailed visual model. In VCSSL, you can implement this by overlaying transparent polygons or models onto your visual model. These simplified models can take forms such as cuboids (bounding boxes) for easier and faster collision checks.

Example Program

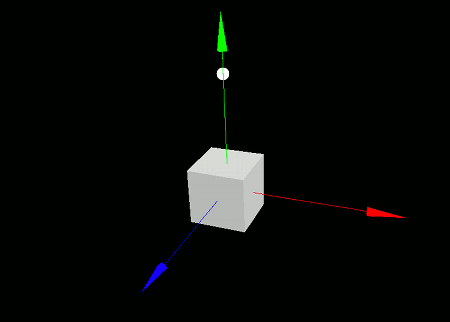
Let's try placing a box-shaped model in world coordinates and simulate a point falling onto it from above, bouncing off its surface.

To do this, we'll use collision detection between a ray and a model. Specifically, we'll cast a downward ray from the falling point (ball), and when the intersection between the ray and the model comes within a certain distance, we'll reverse the falling speed to make it bounce. Try writing and running the following code:

import graphics3d.Graphics3DFramework;
import Graphics3D;
import Math;  // For using the abs function


// Variables for storing IDs of models and polygons
int axis, box, pointPolygon;

// Variables for storing IDs of vectors
int directionVector, pointVector, interVector, normalVector; 

// Variables related to animation and motion
double y = 3.0;   // Height of the point
double v = -0.0;  // Falling speed
double a = -1.0;  // Gravitational acceleration
double dt = 0.05; // Time interval for animation


// Function called at the start of the program
void onStart ( int rendererID ) {

	// Optional: Set window size and background color
	setWindowSize( 800, 600 );
	setBackgroundColor( 0, 0, 0, 255 );

	// Place axis model in the world coordinate system
	axis = newAxisModel( 3.0, 3.0, 3.0 );
	mountModel( axis, rendererID );

	// Place a point polygon to observe the motion
	pointPolygon = newPointPolygon( 0.0, 0.0, 0.0, 0.1 );
	mountPolygon( pointPolygon, rendererID );

	// Place a box model in the world coordinate system
	box = newBoxModel( 1.0, 1.0, 1.0 );
	mountModel( box, rendererID );

	// Prepare the direction vector for collision ray
	directionVector = newVector( 0.0, -1.0, 0.0 );

	// Prepare the origin vector for collision ray
	pointVector = newVector( 0.0, 3.0, 0.0 );

	// Prepare vector for storing intersection result
	interVector = newVector();

	// Prepare vector for storing surface normal
	normalVector = newVector();
}


// Function called repeatedly per frame (dozens of times per second)
void onUpdate (int renderer) {

	// Calculate the falling position of the point
	v += a * dt;
	y += v * dt;

	// Update the origin of the collision ray and the point's position
	setVector( pointVector, 0.0, y, 0.0 );
	setPolygonVector( pointPolygon, 0.0, y, 0.0 );

	// Perform collision detection; returns whether an intersection exists
	bool hit = getModelIntersection( 
			box, directionVector, pointVector, interVector, normalVector
	);

	// If intersection exists and distance is less than 0.2, bounce back
	if( hit ){
			// abs returns the absolute value
			if( abs( getVectorY( interVector ) - y ) < 0.2 ){
					v = abs( v );
			}
	}
}

When you run this program, a white box and a ball will appear on the screen. The ball falls and bounces off the top surface of the box.

Execution Result

The ball starts falling as soon as the program begins and bounces off the surface of the box upon collision.